让学习活动“结构化”

朱满喜

摘要：从一次《间隔排列》教学点线结构的学习活动设计出发，探索块状结构和立体结构的优化设计。教师不应零敲碎打，让学生“小步走”，分散地开展一个接一个的小活动，而应融通多个活动的关联，通过大活动的设计和大问题的引领，让学生“大步走”甚至“一步走”，在更大的开放空间中实现动态、立体的思维发展。

关键词：学习活动;结构化处理;点线结构;块状结构;立体结构

一次教学研讨活动中，笔者观察了一位教师执教的苏教版小学数学三年级上册《间隔排列》一课，对其中学习活动的结构化处理生发了思考。以下呈现三种“步伐”的教学设计及优化思路。

一、点线结构——“小步走”

该教师设计的学习活动如下：

活动1：观察“小兔乐园”情境图，找到其中一一间隔排列的两种物体（小兔和蘑菇、夹子和手帕、木桩和篱笆），数一数，在学习单上填一填每组两种物体的数量。

活动2：观察小兔和蘑菇的排列，说说两种物体的数量为什么相差1？

学生交流。教师引导学生比较不同的方法（数一数、连一连、圈一圈、写数字等），并在比较中发现不同的方法有相同的地方，得出结论：一只小兔对着一个蘑菇，一一对应，最后多了1个。

活动3：观察夹子和手帕、木桩和篱笆，说说为什么都相差1？

学生交流，分别用数一数、连一连、圈一圈、写数字等不同的方法得出结论。

活动4：解决变式问题。

（1）20只小兔站成一排，每两只小兔中间有一个蘑菇，一共有多少个蘑菇？1000只小兔呢？

师生讨论得出结论：小兔比蘑菇多1;20-1=19（个），1000-1=999（个）。

（2）20只小兔站成一排，每两个蘑菇中间有一只小兔，一共有多少个蘑菇？

学生自主得出结论：蘑菇比小兔多1;20+1=21（个）。

教师引导学生对比两道题目的结论发现：首尾相同，两端物体比中间物体数量多1。

（3）如果在最后一个蘑菇后面再加一只小兔，会发生什么变化？

学生发现：首尾不同，两种物体数量相等。

活动5：回顾刚才探索和发现规律的过程，说说体会。

实际执教时发现，教学时间不够。课后交流时，该教师表示，这节课容量很大，既要认识一一间隔排列现象，也要发现一一对应数量相差的原因，还要了解首尾相同和首尾不同两种情况，在教学时间安排上有很大困难。这也是很多教师常有的难题：一节课只有40分钟，但是要讲的知识很多，还要让学生去动手操作、小组合作、活动探究，时间根本安排不过来。

不难看出，本节课中，教师比较注重学生主体地位的落实，对每个学习活动都大胆放手，让学生去探索、去表达，还注意引导学生用不同的方法来发现“一一对应”的特点。然而，本节课单新授环节就设置了5个学习活动，其中活动4又通过3道变式题一步步地引导学生发现间隔排列的两种不同情况。这是非常典型的点线结构的学习活动设计：将一个知识点分成几个小点，每一小点都让学生“小步走”探究。因此，时间不够是很自然的。更重要的是，课堂结构的线形也就决定了学生的思维和认知也是单一、纵向发展的，前后知识之间没有横向的联通整合。尽管让学生去自主探究，但是如果学习活动的开放空间不够，其实还是教师在牵着学生走。

二、块状结构——“大步走”

针对上述问题，我们研讨出了如下调整方案：

活动1：观察“小兔乐园”情境图，找到其中一一间隔排列的两种物体，数一数，在学习单上填一填每组两种物体的数量。

活动2：观察小兔和蘑菇、夹子和手帕、木桩和篱笆的排列，说说每组两种物体的数量为什么相差1？

活动3：解决变式问题（同前）。

也就是把之前的活动2、3并成一个“大步”，让学生从多个例子中发现共同的特点：两种物体间隔排列，三组都存在“一一对应”关系。这样的合并能达到“1+1>2”的效果——不仅两种物体的数量关系容易被发现，而且从多个例子中可以归纳发现间隔排列的特点，这样得出的结论也更具说服力。

几个例子放在一起归纳发现一些数学规律，进而去验证、去运用，即为块状结构的学习活动。其在一些需要思维进阶比较大的新授教学中，是非常适用的。前一“块”学习活动引导学生初步感知新知，后一“块”学习活动引导学生在初步掌握知识后进一步发展思维。

三、立体结构——“一步走”

而后，笔者继续对学习活动的结构化处理做了深入思考。笔者更倾向于设计一个大活动，把“一一对应”与“首尾相同和首尾不同两种情况”放在一起让学生“一步走”。因为这两“块”内容本身讲的是同一个知识，“一一对应”是间隔排列的内在特点，“首尾的物体和数量差异”是间隔排列的外在呈现，两者应该融通放在一个综合活动中。具体设计如下：

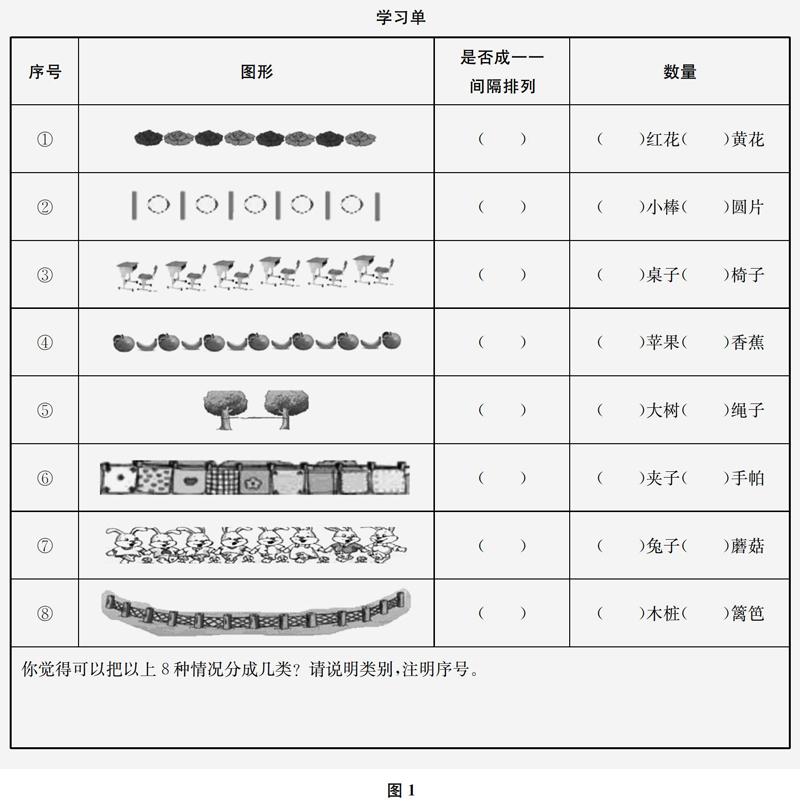
设计并分发学习单（如下页图1），让学生完成。

（1）数一数每组间隔排列的两种物体的数量，然后进行分类，并说明分类原因。（预设：学生分成首尾相同和首尾不同两类。）

（2）对比两类图形的排列规律，说说数量之间有什么特点？（引导发现：间隔排列都是两种物体一一对应，当对应分组后，没有多余就是两种物体数量相同，开头是第一个物体，结束在第二个物体，首尾不同;当对应分组后，末尾多一个，多的就是开头的那种物体，首尾相同。）

立體结构的学习活动，是具有丰富内涵、智慧灵动和生命活力的学习活动，更加注重学生思维过程的全面性。学生在这样一个开放性、综合性的学习活动中展开探究，一步到位，可使生成更加动态精彩，知识掌握更为立体。

综上可以看出，点线结构的学习活动，不利于数学知识间的融通，把知识打散了，把思路切割了。这使得学生在教师早已框好的狭小空间中完成探究。而块状结构和立体结构的学习活动，生成空间就会大很多。两种活动在具体教学中各有千秋，根据不同教学内容的特点可以采用不同的结构化处理。一般来说，如果知识的思维跨度大，有必要先通过一个探究活动完成初步发现，累积一定经验后再进行下一个探究活动，这样的内容更适合设计块状结构的学习活动;如果知识联系紧密，相互可以证明、引发，则可以设置一个立体结构的学习活动，给出一个大空间，让学生自主发现其中数学本质和表象之间的关系。

课堂的有效性更多的是看课堂具体行进的状态以及教师处理问题的方式。教师不应零敲碎打，让学生“小步走”，分散地开展一个接一个的小活动，而应融通多个活动的关联，通过大活动的设计和大问题的引领，让学生“大步走”甚至“一步走”，在更大的开放空间中实现综合、立体的思维发展。