例谈小学数学教学中促进深度学习的策略

胡文兰

摘要：深度学习具有积极参与、充分体验、意义建构、迁移应用等特征。在小学数学教学中，可以采取以下策略促进学生的深度学习：利用问题驱动，促进积极参与;设计丰富活动，促进充分体验;抓住知识联系，促进意义建构;设计变式练习，促进迁移应用。

关键词：深度学习;小学数学;问题驱动;知识联系;变式练习

北京师范大学郭华教授指出，深度学习“是指在教师引领下，学生围绕具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程”。西北师范大学安富海教授认为：“深度学习是一种基于理解的学习，是指学习者以高阶思维的发展和实际问题的解决为目标，以整合的知识为内容，积极主动地、批判性地学习新的知识和思想，并将它们融入原有的认知结构中，且能将已有的知识迁移到新的情境中的一种学习。”综合看来，深度学习具有积极参与、充分体验、意义建构、迁移应用等特征。因此，笔者在小学数学教学中，主要采取以下策略促进学生的深度学习。

一、利用问题驱动，促进积极参与

深度学习是积极参与、主动探究的学习。“学起于思，思源于疑。”教师可以利用问题驱动，促进学生积极参与、主动探究。特级教师黄爱华说过：“大问题的一个核心追求是让学生不教而自会学，不提而自会问。”所以，教师可以设计一些指向核心知识（教学重、难点）的“大问题”，引领整节课的教学，促使学生不仅分析和解决问题，而且发现和提出问题，从而构建“问学现场”，即围绕各种问题展开深度学习。

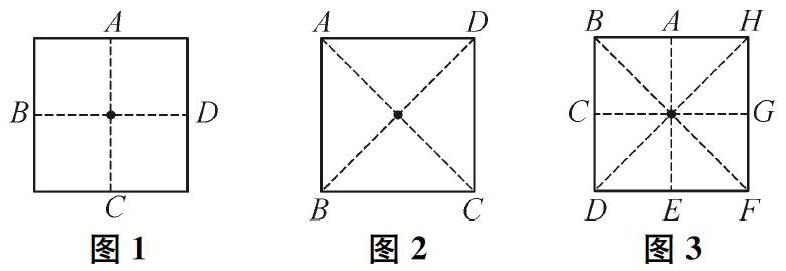
例如，《圆的认识》一课伊始，笔者提出如下问题：（1）有4个人参加投球入篓游戏，如图1、图2所示的两种站位设计（图中正方形中心为球篓所在，字母标示处为投球者站位）公平吗？为什么？（2）如果是8个人参加投球入篓游戏，如图3所示的站位设计（图中正方形中心为球篓所在，字母标示处为投球者站位）公平吗？为什么？（3）学习了今天的内容后，你能不能为他们找到公平的站位设计方案呢？

这组问题层层递进，最终指向这节课的核心知识，即圆的特征：同一个圆的半径都相等。课堂伊始提出这个问题，促使学生全程积极参与、主动探究。认识了圆的特征后，学生就迫不及待地提出：可以将球篓放在圆心位置上，投球的人站在圆上任意一点位置上投球，这样根据圆的半径处处相等的特点，可以确定每个人投球的距离一样，游戏具有公平性。

笔者顺势问道：你还能提出哪些和圆的这个特征相关的问题来考一考大家？学生稍作思考后，七嘴八舌地抛出了自己的问题：为什么车轮要设计成圆形，而不设计成正方形、三角形等其他形状？怎样在操场上画一个直径是10米的圆？……这样的“问学现场”促使学生主动探究，深化了学生的思维，提升了学生对圆的特征的认识。

二、设计丰富活动，促进充分体验

深度学习是充分体验、激发感悟的学习。“我听到了，我忘记了;我看到了，我记住了;我做过了，我理解了。”活动，是认识发展的直接源泉和根本途径。因此，教师应该设计多感官参与的活动，让学生亲身经历，促进学生充分体验、激发感悟。

例如，教学《时、分、秒》一课时，让学生在一分钟内完成跳绳、做口算题、朗读课文、写字等活动，体验1分钟有多长;教学《千克与克》一课时，让学生掂一掂重约1克的回形针，掂一掂重约50克的鸡蛋，提一提重约1千克的一袋面粉，搬一搬重约5千克的一袋大米，体验千克与克分别适用于什么物体的重量计量;教学《米和厘米》一课时，让学生用米尺分别标记1米高在自己身体上的位置、在教师身体上的位置，体验1米的不变性与人体的多样性;教学《面积单位》一课时，让学生紧挨着站在一起感受1平方米有多大，让学生手拉手围成一圈感受100平方米的大小……这样的活动体验不仅能促进学生对较小计量单位的感知理解，而且能为学生想象理解较大计量单位奠定基础。

再如，教学“正、反比例”内容后，笔者组织学生分组完成设计树木“身份证”的活动：首先引导学生猜想、验证“同一时间、同一地点，物体的影长与实际高度的比值一定”，然后引导学生据此测量、计算树木的实际高度，作为树木“身份证”中的一项重要信息。这样手脑并用的活动体验激活了学生的高阶思维，促进了学生的深度学习。

三、抓住知识联系，促进意义建构

深度学习是意义建构的学习，应从个人的原有认知结构出发，加工新的知识，并将其融入原有认知结构。因此，教师要抓住知识之间的联系，促进学生利用旧知获得新知（温故知新），完成意义建构。此外，还要启发学生抓住知识之间的联系，灵活转换知识，获得解题思路。

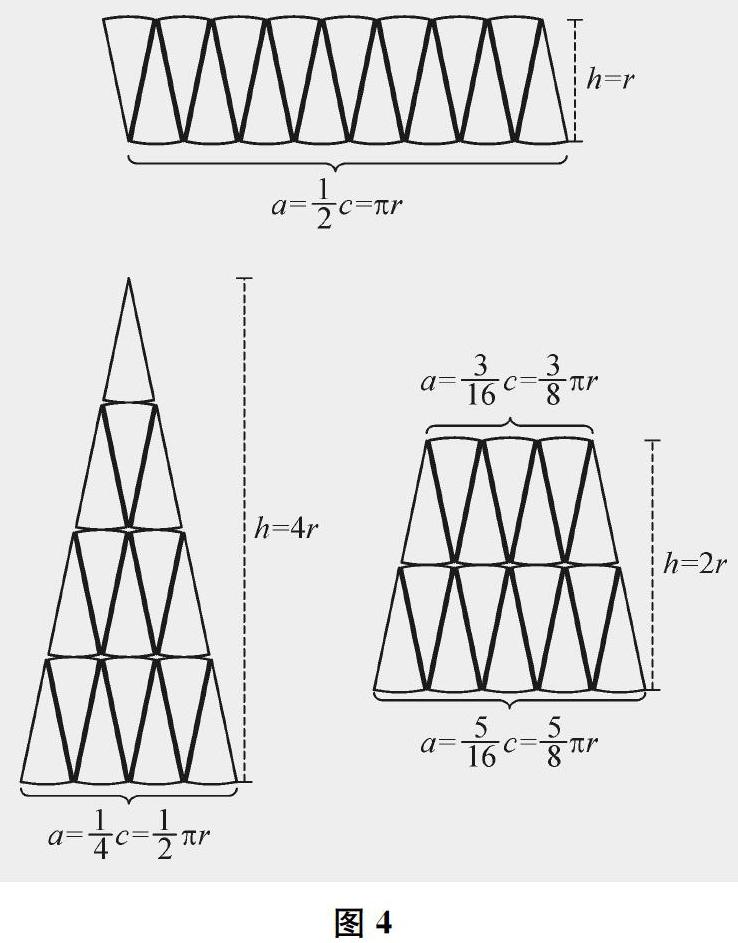
例如，教学《圆的面积》一课时，笔者引导学生开放思考：除了像教材给出的那样将圆转化为长方形，还可以将其转化为什么图形，从而推导出其面積计算公式？学生积极思考与尝试，进而在分享与交流中，理顺了圆与平行四边形、三角形、梯形的转化关系（参见图4），还将其与转化为长方形的方法做比较，从而完善了知识结构，培养了发散思维，实现了深度学习。

再如，解决有关分数的实际问题一直是学生学习的难点，很多学生常常无法正确判断单位“1”，导致在计算的选择与量率的对应上出错。为了突破这个难点，教学《比的认识》一课后，笔者精选学生易错的有关分数的实际问题，编制题组练习，引导学生根据分数与比的关系，将分数关系转化为比的关系，通过寻找不变量搭桥，找准对应份数来解决。例如，一组练习为：“学校开展兴趣小组活动。第一周，美术组的人数是音乐组的23。（1）第二周，又有12人参加了音乐组，这时美术组的人数是音乐组的12，则原来美术组和音乐组各有多少人？（2）第二周，美术组的4人调到了音乐组，这时美术组的人数是音乐组的12，则原来美术组和音乐组各有多少人？”在笔者的引导下，学生得到如图5所示的解法。这里，学生不仅理顺了分数与比的关系，而且通过分数与比的转化，找到了解决此类问题的有效方法。

四、设计变式练习，促进迁移应用

深度学习是迁移应用的学习，应将已有知识迁移到新的情境中，用来解决新的问题。一般来说，新的情境问题相对于生成已有知识的情境问题都会发生变化。因此，迁移应用可能是积极有效的（正迁移），也可能是消极无效的（负迁移）。对此，教师要设计多样的变式练习（包括近迁移题、中迁移题、远迁移题），提升学生掌握相关知识的概括化程度和迁移应用的灵活性，帮助学生打破思维定式，实现正迁移。

例如，教学“正、反比例”内容后，笔者创编如下题目：“电视机屏幕的规格是指对角线的长度，一般用英寸来表示（1英寸≈2.54厘米），屏幕的长宽比为16∶9，如50英寸是指电视屏幕的对角线长50英寸，其长约为112厘米，宽约为63厘米。那么，65英寸电视机屏幕的长约是（）厘米，宽约是（）厘米。”面对繁多的题目信息，学生先是一筹莫展，然后想到刚学习的正比例知识，试图利用屏幕的长宽比为16∶9来解决，但是，发现要求长和宽两个量，仅用这个条件是不够的。于是，有学生关注到对角线长65英寸，试图将其化为厘米后运用超前学习的初中知识——勾股定理来解决。笔者提示学生画图，学生终于想到更早学习的图形放大、缩小和比例知识，从而利用两种电视机屏幕的长、宽、对角线成比例来解决。

再如，教学《比较分数的大小》一课时，学生掌握同分母分数比较大小和通分后，面对异分母分数比较大小的题目，总是想到转化成同分母分数再比较。对此，笔者设计变式题组，引导学生学会根据不同的分数特征，选择不同的比较方法：（1）一个真分数和一个假分数，直接比;（2）和1相差相同个分数单位的两个分数，和中间量 1比;（3）一个大于12，一个小于12，和中间量12比;（4）分母较大的两个分数，分子通分后再比较;（5）两个假分数，转化成带分数后，先比较整数部分，再比较真分数部分;（6）多个分数、小数排序，转化成小数再比较。

参考文献：

[1] 沈重予，王林.小学数学内容分析与教学指导[M].南京：江苏凤凰教育出版社，2015.

[2] 郭华.深度学习及其意义[J].课程·教材·教法，2016（11）.

[3] 安富海.促进深度学习的课堂教学策略研究[J].课程·教材·教法，2014（11）.

[4] 张姝华，喻平.问题解决中迁移的心理学研究及其对中学数学教学的启示[J].教育研究与评论（中学教育教学），2019（9）.