初中数学直观化教学研究

孙明丽

摘要：数学教学要采用直观化手段，充分调动学生的多种感官，让学生获取足够的感知体验和表象知识，进而上升为思维活动和本质认识。在初中数学教学中，具体而言，可提供实物模型、静态图形、动态图形、表格等直观材料，发挥视觉效能;设计直观活动，促进多感官协同。

关键词：直观化教学;初中数学;材料;活动

数学作为抽象性和逻辑性较强的一门学科，在培养学生的思维能力方面发挥着重要作用。从思维的角度看，数学学习有一个从具体形象到抽象逻辑的过程。直观思维是指基于具体的、可直接感知的事物和形象所进行的思维活动。因此，数学教学要采用直观化手段，充分调动学生的多种感官，让学生获取足够的感知体验和表象知识，进而上升为思维活动和本质认识。下面结合初中数学教学实践，具体谈谈笔者的做法。

一、提供直观材料，发挥视觉效能

视觉是个体接收外界信息的主要感官通道。从狭义上看，直观化教学就是为学生提供丰富的直观材料，通过视觉感知体验，激活学生的数学思维，促进学生的数学理解。事实上，很多数学内容都具备直观化的基础。具体来说，教师可以提供的直观材料可以分为以下几类：

首先是实物模型。几何教学中，可以提供或让学生参与制作基本图形的实物模型，让学生在观察、操作中感受它们的特征、属性和关系。例如，教学“特殊的平行四边形”时，要求学生根据定义画出并剪下每种图形的具体模型，对这些图形的边、角、对角线进行测量、比较，从看得见、摸得着的实物模型中体会这些图形并且加以区分。再如，教学“轴对称图形”时，让学生自主制作实物模型，通过折叠体会轴对称性，为后续的说理证明打下基础。

其次是静态图形。代数教学中，可以引导学生见“数”想“形”，转化得到几何图形。转化的方式之一是利用解析几何思想，把数变成坐标系中的点;之二是考虑几何意义，把数与式看成图形的度量（长度、面积、体积等）。这是数形结合思想的重要体现，此处不再举例赘述。值得一提的是，从起源和本质上看，符号其实是图形的进一步简化和浓缩，不仅具有抽象化、形式化的特征，也具有一定的直观化、形象化特征。教学中，教师尤其可以设计一些具有视觉冲击力的符号系统（组合），帮助学生理解有关知识。例如，学习因式分解时，学生常常出现结果不全为乘积形式的错误，这是没有理解透彻因式分解的定义。教学中，教师可以呈现“++=（）（）…（）”的符号系统，让学生比较直观地把握因式分解的实质。

再次是动态图形。利用信息技术呈现动态图形，能够帮助学生更好地理解具有过程内涵的知识。例如，观察一次函数y=kx+b（k>0）的大致图像时，学生常常以为右上方是作图起点，从而得出图像下降（函数单调减）的错误结论。教学中，教师可以利用信息技术演示作图过程，帮助学生了解函数图像从左到右的作图顺序，领悟图像趋势（函数单调性）从左到右的观察方法。这里需要说明的是，有些过程内涵虽然不是动态图形，但是也具有一定的直观化、形象化特征。教学中，教师应该将它们完整地呈现出来，避免学生的认识出现偏差。比如，解方程或方程組时，不仅要用文字阐述演算步骤，而且要用算式完整呈现演算过程。例如，解方程x2-y+13=1时，完整呈现演算步骤和过程“两边同乘6，得x2×6-y+13×6=1×6”，避免学生出现“右边常数项漏乘6”的错误。

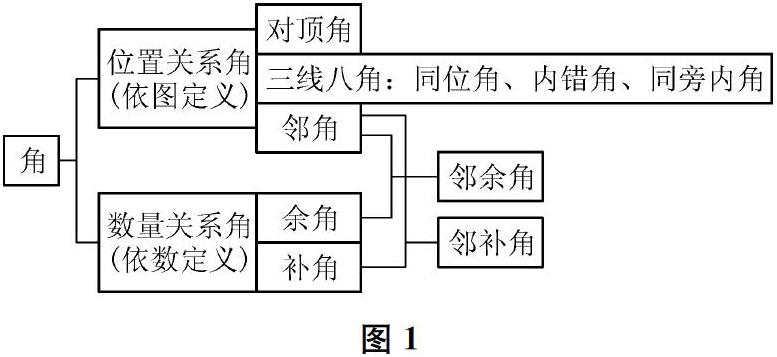
最后是表格。表格也可以作为一种直观材料。它能简洁地呈现出关键信息，并便于联系比较信息。由此，可以进一步提炼、发挥，形成知识结构图或思维导图。在章节复习教学中，可以通过表格整理呈现基本知识点及其相互关系，使之更加清晰有序，更加一目了然，帮助学生“由厚到薄”，整体把握知识体系和思维方法。例如，复习苏科版初中数学七年级上册第6章《平面图形的认识（一）》时，可以通过列表，汇总整理得到图1，直观地表示出各种角的区别和联系。此外，在信息量大的“阅读理解题”（如实际应用题）的解题教学中，可以借助表格归类提取信息，分析相互关系，从而彰显思考过程，获取解题思路。

二、设计直观活动，促进多感官协同

心理学研究表明，多种感官协同参与的活动较之单一感官参与的活动在大脑皮层中留下的痕迹要深刻得多。从广义上看，直观化教学则是为学生设计丰富的直观活动，帮助学生通过多感官协同的感知体验，激活数学思维，促进数学理解。

例如，教学“三角形全等的条件”时，让学生独立探索，根据条件的个数、类型逐一展开探究。对于每种情况，让学生画出并剪下两个三角形模型，再进行平移、旋转、翻折等操作，从而通过图形的比较，猜测和验证结论，对三角形全等的条件形成系统深刻的认识。

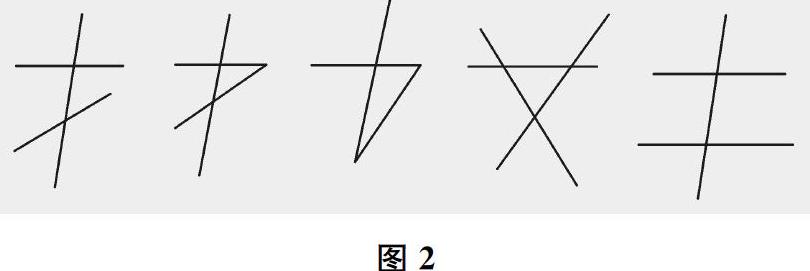
再如，教学“同位角、内错角、同旁内角”时，先给每个学生三根小棒，让他们尝试摆出各种情况（如图2），通过找截线来确定各类角，准确把握各类角的定义;再给每个学生一根小棒，让他们在原有图形的基础上继续搭建并确定各类角，进一步体会“三线八角”的准确内涵。

参考文献：

[1] 方薇燕.论数学直观思维及培养[J].学子（教育新理念），2013（17）.

[2] 沈晓生.数学基本活动经验从哪里来？——例谈培养学生获取数学基本活动经验的三条路径[J].中学数学，2019（2）.

[3] 孙红强.图形：培养直观想象素养的关键要素[J].教育研究与评论（中学教育教学），2020（3）.