Sobolev方程的等参有限元法
刘智新,张媛,宋士仓
(1.郑州大学数学与统计学院,河南郑州450001;2.郑州铁路职业技术学院数学教研室,河南郑州451460)
1.引言
考虑如下的Sobolev方程

其中Ω⊂R2为具有光滑边界∂Ω的有界区域,X=(x,y),u0(X),f(X,t)是已知函数.
Sobolev方程在流体穿过裂缝岩石的渗透理论,土壤中的湿气迁移问题,不同介质中的热传导问题,黏土的加固理论等许多数学物理问题中有着广泛的应用.关于其数值方法的研究已经有很多,如文[1]讨论了标准混合有限元方法,文[2-3]介绍了H1-Galerkin混合有限元方法,文[4-5]分别讨论了非协调元方法和弱Galerkin有限元方法.进一步的,文[6-8]讨论了非线性的情形,并给出了相应数值方法的收敛性分析.关于这些数值方法的文献还有很多,但这些文献主要是在凸多边形区域上讨论的.对于多角形区域,由于解的光滑性不够,不宜采用高次元去逼近,否则达不到提高精度的目的.在实际生活中会经常遇到曲边区域的情况,当用有限元方法去处理时,通常的方法是用多角形区域(直边有限元)去逼近,但由于边界处的误差较大,也会影响精度.若通过对边界处的网格加密来减少误差,这样也会导致计算量的巨大增加.因此为了使收敛阶不受损失,我们可以采用等参有限元去逼近曲边区域.
目前讨论等参有限元逼近的文献也比较多,在此我们简要描述与之相关的一些主要贡献.设u是某个方程的变分问题的解,Ω是具有光滑边界的有界区域,uh和Ωh分别是u和Ω的近似值.文[9-10]中详细介绍了等参有限元方法,并应用二次Lagrange等参元去逼近具有齐次Dirichlet边界的二阶椭圆问题,最终得到了‖-uh‖H1(Ωh)=O(h2)的误差估计,其中~u是u到Ωh的某种延拓.同时由于其考虑了数值积分,因此只要积分点位于Ω∩Ωh上,便能够定义近似问题而无需将函数延拓到Ωh上,文[11]给出了不使用数值积分的误差估计.基于这种思想,许多学者将等参有限元方法应用到其他问题中,如[12-14]讨论了用等参混合有限元方法去求解四阶椭圆边值问题和Stokes问题,得到了与凸多边形区域上同样的收敛阶.文[15-16]将等参有限元方法应用到了椭圆界面问题中,得到了比传统的有限元方法更好的收敛阶.进一步的,文[17]在文[10]中介绍的等参有限元方法基础上,提出了另一种估计思路.它讨论了如何去构造一个映射Φh:Ωh→Ω,该映射对于任意维数空间都是有效的,可以很自然的将Ω区域上的函数延拓到Ωh上,并给出了相关的误差估计.然后应用k次Lagrange等参元讨论了曲边区域上的二阶椭圆问题,得到了‖u-uh°‖H1(Ω)=O(hk)的误差估计.但是以上讨论都是基于定常问题,就作者所知,将等参有限元方法应用于非定常问题的文献还比较少,文[18]基于文[10]中提出的思想讨论了抛物方程的等参有限元方法,其中引入了Ritz投影,并给出了严格的证明,最后讨论了全离散格式下真解和有限元解在Ω∩Ωh上的L2模误差估计.文[19]将文[17]中的思想进一步应用到了抛物方程中,并分别讨论了真解和有限元解在半离散和Crank-Nicolson全离散格式下的误差估计.但上述文献只是给出了理论估计,并没有给出相应的数值算例.
本文主要研究当求解区域Ω⊂R2为具有光滑边界∂Ω的有界区域时,应用文[17]的思想去求解问题(1.1).给出了半离散问题和向后欧拉全离散格式下解的存在唯一性的证明,并且分别讨论了真解和有限元解之间的误差估计.最后给出了一个数值算例,进一步验证了理论分析的结果,其结果表明,采用等参有限元去逼近曲边区域可以达到和凸多边形区域上同样的收敛阶.
在本文中我们用C表示一个与h无关的大于0的常数,不同的地方大小可能不同.
2.预备知识
为了下面证明的需要和方便,首先给出一些定义和引理.
我们用Wm,p(Ω)表示通常的Sobolev空间,其中m≥0,1≤p≤∞,其范数定义如下

当p=2时,记Wm,p(Ω)=Hm(Ω).并且相关的范数记作如下:

设Y是Banach空间,其范数记为‖·‖Y,对映射φ:[0,T]→Y,定义

为了引进全离散逼近格式,将区间[0,T]划分为:0=t0<t1<···<tN=T,Δt=为时间步长,其中N为正整数.同样定义

另外关于等参有限元的详细介绍可见文[9-10],此处不再详细介绍.现在我们用k次Lagrange等参有限元对区域Ω进行剖分,Jh为一族正则的等参有限元剖分,Ω的近似区域为Ωh=其中T为剖分单元,记h为剖分单元的最大直径.我们记ΠT为单元T上的插值算子,其具体定义可见文[9-10],又由文[17]知,存在可逆映射Φh:Ωh→Ω,其逆为则有Φh|T:T→,且同理,有Φh:→X.定义Πh为整个Ωh区域上的插值算子,对则有

由此引入(Ωh)的有限维子空间

及)的有限维子空间
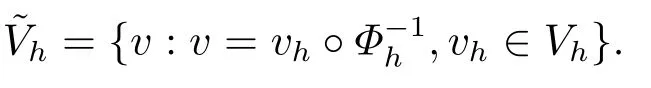
由文[17],我们可以得到如下三个引理.
引理2.1设Jh为一族正则的等参有限元剖分,用J(Φh)表示映射Φh的Jacobi行列式,则存在一个与h无关的常数C,使得
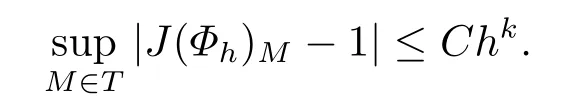
引理2.2假设v∈C0(∩Hk+1(Ω),令则存在一个与h无关的常数C,然后有

引理2.3设0≤m≤k+1,则范数‖vh‖Hm(Ωh)和是等价的.
3.半离散问题的误差估计
问题(1.1)的变分问题为,求u:[0,T](Ω),使得

则问题(3.1)对应的半离散逼近格式为:求uh:[0,T]→Vh,满足
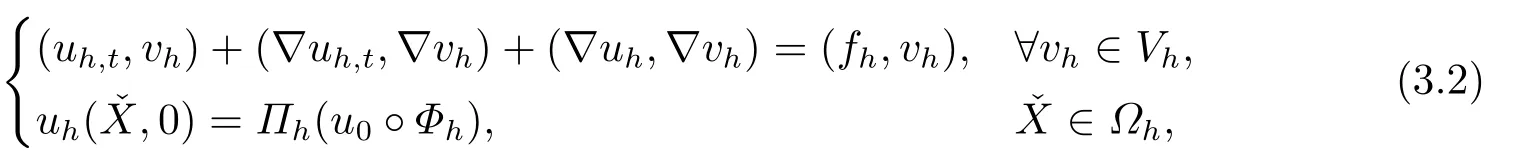
定理3.1问题(3.2)有唯一解.
证设是空间Vh的一组基,则uh可以表示为
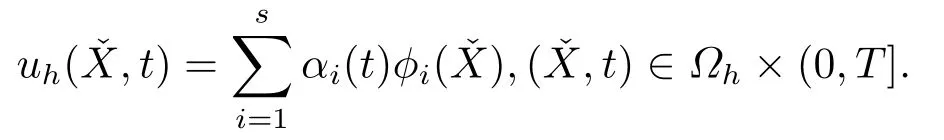

其中

显然(3.3)式是关于未知函数α(t)的线性常微分方程组,当给定初值α(0)时,由常微分方程理论知(3.3)式存在唯一解α(t),从而半离散问题(3.2)存在唯一解uh(X,t).
定理3.2设u和uh是问题(3.1)和问题(3.2)的解,f∈L2(0,T,L2(Ω)),u∈L2(0,T,Hk+1(Ω)),ut∈L2(0,T,Hk+1(Ω)),并且ut,∇ut,∇u有界,则有如下估计
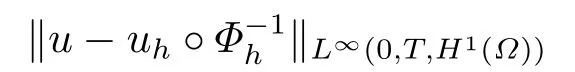
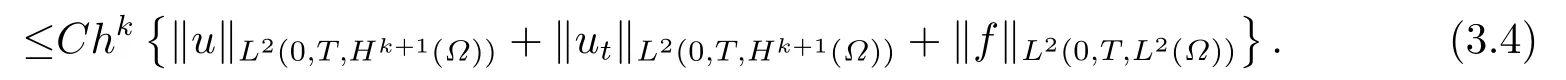
证首先我们引入一个稳态问题,即寻求辅助函数χh∈Vh,使得

令u°Φh-uh=u°Φh-χh+χh-uh=θ+η,其中θ=u°Φh-χh,η=χh-uh.将(3.1)式改写为

(3.5)式减去(3.2)式得

其中G1=(∇χh,t,∇vh)-(∇ut,∇(vh°)),G2=(∇χh,∇vh)-(∇u,∇(vh°)),G3=.
在(3.5)式中令vh=η,则左端为


同理

将(3.8)-(3.11)式代入(3.5)式,则有

将(3.12)式从0到t积分,可得

利用Gronwall引理,存在常数C,使如下估计式成立

对于辅助函数χh,因为Πh(u°Φh)∈Vh,且满足(∇(Πh(u°Φh)),ωh)=(∇(u°Φh),ωh),∀ωh∈Vh.所以我们取χh=Πh(u°Φh),由引理2.2有

又θt=ut°Φh-Πh(ut°Φh),类似地有


应用引理2.3即可得到(3.4)式,定理证毕.
4.全离散问题的误差估计
现在我们采用向后欧拉差分格式构造问题(3.1)的全离散格式,目的是求解初边值问题的真解u(x,t)在节点tn,n=1,2,...N处的近似值.对于[0,T]上的任意光滑函数φ,定义φn=
与问题(3.1)对应的的全离散逼近格式为:求Un∈Vh,n=0,1,...N,使得

在(3.1)式中令t=tn,可得
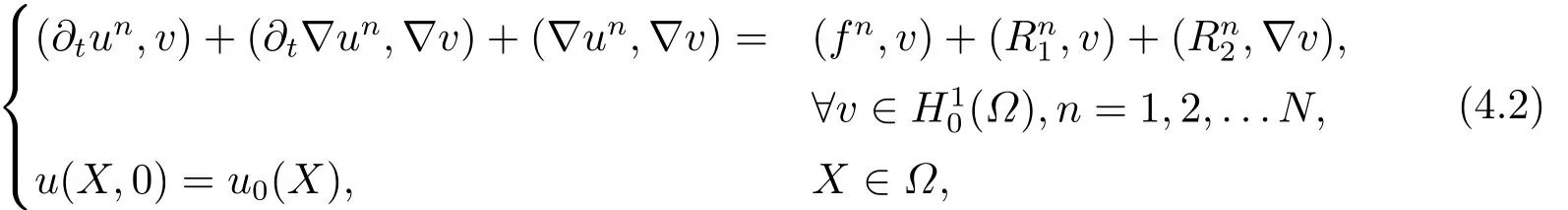
定理4.1问题(4.1)有唯一解.
证记则全离散问题(4.1)可以等价的表示为:求Un∈Vh,n=0,1,···N,使得

又

从而A()是Vh上的正定双线性型,易证A()是Vh上的连续双线性泛函,而且对于已知的Un-1,F()是Vh上的连续线性泛函.于是由Lax-Milgram定理知,方程(4.3)即问题(4.1)存在唯一的解Un∈Vh,n=0,1,...N.
定理4.2设un和Un是问题(4.2)和问题(4.1)的解,f∈L2(0,T,L2(Ω)),u∈L2(0,T,Hk+1(Ω)),ut∈L2(0,T,Hk+1(Ω)),utt∈L2(0,T,H1(Ω)),并且∇u有界,则对任意的1≤n≤N,有如下估计

证此处同样引入辅助函数使得

记un°Φh-Un=un°Φh-Wn+Wn-Un=θn+ηn,其中θn=un°Φh-Wn,ηn=Wn-Un.将(4.2)式改写为

(4.5)式减去(4.1)式,可得

然后,在(4.6)式中令vh=ηn,则有

对于(4.7)式左端,有

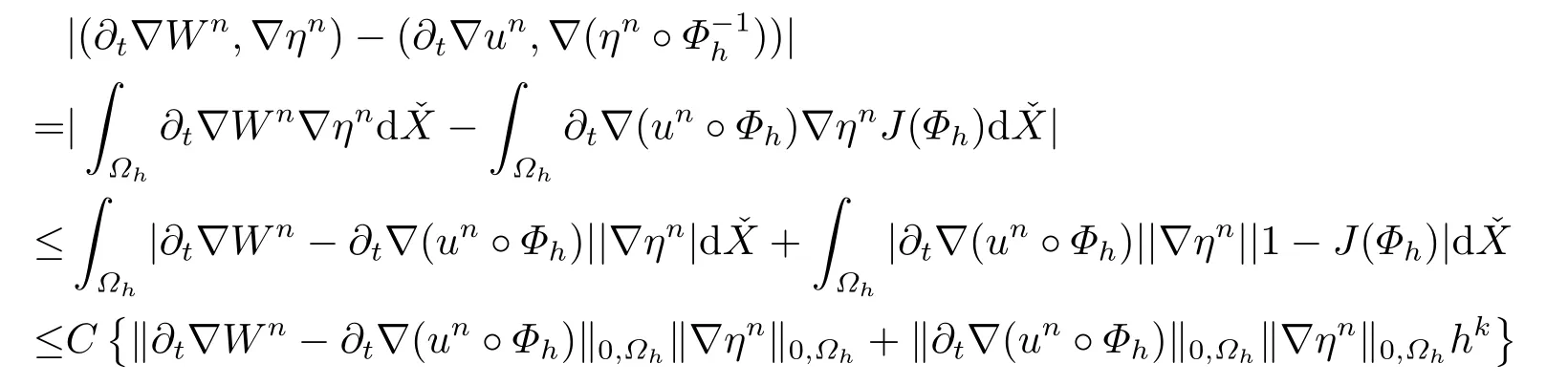

同理

结合(4.7)-(4.13)式,可得
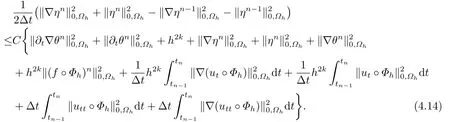
(4.14)式两端同乘以2Δt,并对n从1到m求和,有

则由离散的Gronwall引理可得


因此
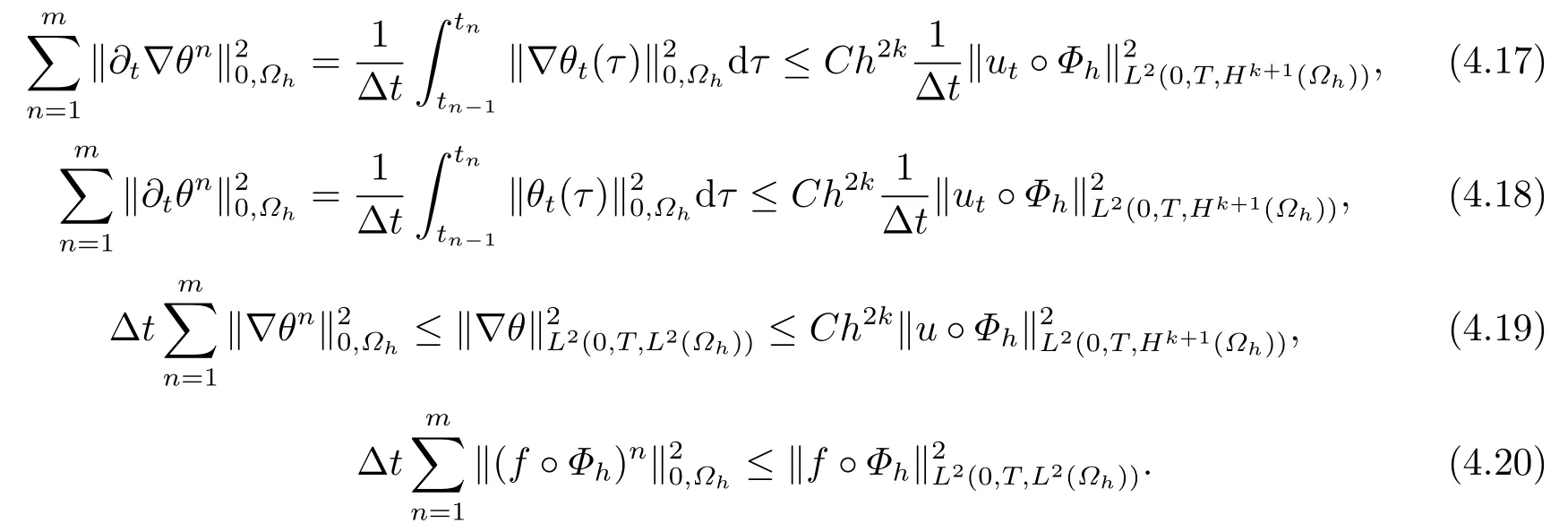
又注意到∇η0=η0=0,则结合(4.16)-(4.20)式,对任意的1≤n≤N,有

最后由引理2.3及三角不等式即可得到(4.4)式,定理4.2得证.
5.数值算例
为了验证理论分析的正确性,我们首先考虑问题(1.1),其中

可以容易验证其真解为

然后为了便于数值计算,我们选用二次Lagrange等参元.对空间区域Ω沿x轴和y轴方向剖分成M×M(M=2,4,8,···)份,采用向后欧拉格式对时间区域进行离散,其中如图5.1所示是一个4×4的二次等参元网格剖分图.

图5.1 4×4网格图
图5.2和图5.3分别给出了t=0.1,网格剖分为16×16时问题(1.1)的真解和问题(4.1)的有限元解.表5.1给出了在不同网格剖分下的误差和收敛阶数,从表5.1中可以看出当网格步长h→0时,收敛阶为O(h2),这和我们前面的理论估计是一致的.

表5.1 t=0.1时的逼近结果

图5.2 t=0.1时真解u

图5.3 t=0.1时有限元解U
- 应用数学的其它文章
- A New Class of Estimators for Extreme Value Index
- 一类具记忆项和非线性阻尼项的双曲型方程的整体吸引子
- 时间分数阶Fisher型非线性种群扩散模型的近似解
- A Line Search Method with Dwindling Filter Technique for Solving Nonlinear Constrained Optimization
- Martingale Transforms on Variable Exponents Martingale Hardy-Lorentz Spaces
- fmKdV Equation for Solitary Rossby Waves and Its Analytical Solution

