Wolfe线搜索下的两类修正FR谱共轭梯度法

夏丽娜朱志斌

(1.桂林电子科技大学数学与计算科学学院，广西桂林541004;2.广西高校数据分析与计算重点实验室，广西桂林541004)

1.引言

考虑无约束优化问题:

其中f:Rn→R为连续可微目标函数，其梯度函数记为g:Rn→Rn.共轭梯度法具有算法结构简单、所需要的计算存储量空间少等优点，其一般迭代格式为:

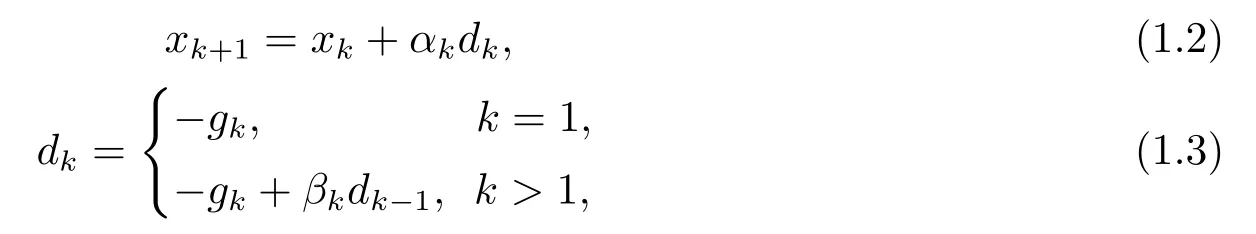
其中xk是第k次迭代点，αk是搜索步长，dk是搜索方向，βk是共轭参数.关于βk的著名公式有

这里yk－1=gk-gk－1，‖·‖为欧氏范数.上面对应的算法分别是Flecher-Reeves(FR)方法[1]、Dai-Yuan(DY)方法[2]、Conjugate-Descent(CD)方法[3]、Polak-Ribi`ere-Polyak(PRP)方法[4，5]、Hestenes-Stiefel(HS)方法[6]和Liu-Storey(LS)方法[7].对于非凸的目标函数，这六个方法在数值表现和收敛性上有很大的差别.其中，FR方法、DY方法和CD方法具有良好的收敛性质，而PRP方法、HS方法和LS方法具有良好的数值表现性质.为了寻求兼具良好数值实验和收敛性质的方法，研究者在上述方法的基础上进行了大量的研究，对βk进行改进推出具有不同效果的方法.如文[8]提出一种修正的PRP共轭梯度法，文[9]提出了两种修正的DY共轭梯度法，文[10]基于Dai-Liao参数提出三种不同的共轭梯度法.

文[11-13]提出一种谱共轭梯度法，其方向迭代由(1.3)式推广为

其中θk为谱参数.

文[14]中讨论了如下形式的谱共轭梯度法：

其中c为大于0的参数.

文[15]中讨论了如下形式的谱共轭梯度法：

其中rk为向量gk与dk－1的夹角.

文[16]在FR方法的基础上提出了两种修正的FR谱共轭梯度法如下：

其中rk为向量gk与dk－1的夹角.

受文[14-16]的启发，以及在文[16]中βk，和的基础上，提出了新的共轭参数和谱参数：

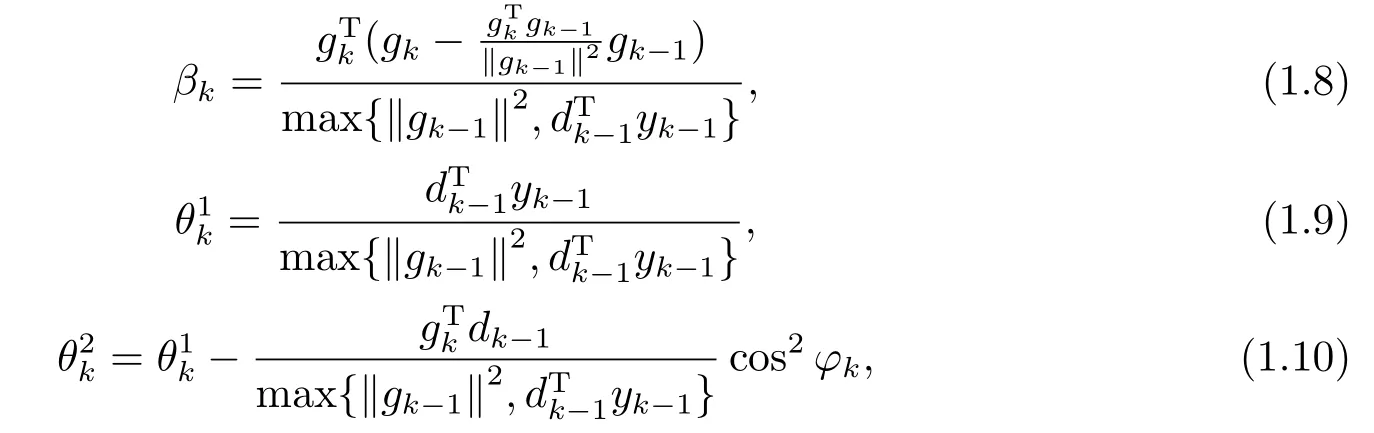
其中φk为向量gk与gk－1的夹角.

本文采用标准的Wolfe线搜索：

其中0＜δ＜σ＜1.

本文提出两个修正的谱共轭梯度法，基于(1.8)，(1.9)，(1.11)和(1.12)的谱共轭梯度法称为ZFR1方法，基于(1.8)，(1.10)，(1.11)和(1.12)的谱共轭梯度法称为ZFR2方法.

为了证明ZFR1方法和ZFR2方法具有全局收敛性，要求目标函数f(x)满足如下假设:

(H1)f(x)在水平集Ω={x∈Rn|f(x)≤f(x1)}上有下界.

(H2)f(x)在Ω的一个邻域内是连续可微的，且它的梯度g(x)满足Lipschitz条件，即存在一个常数L＞0，使得‖g(x)-g(y)‖≤L‖x-y‖，∀x，y∈Ω.

本文余下内容组织如下:在第2节和第3节中，将给出ZFR1方法和ZFR2方法在标准Wolfe线搜索下的性质及其全局收敛性;在第4节中，数值结果验证了这两个方法是有效的.

2.ZFR1方法及其全局收敛性

算法2.1(ZFR1谱共轭梯度算法)

步1 给定初值x1∈Rn，δ∈(0)，ε≥0，d1=-g1，k=1;若‖gk‖≤ε，停止.

步2 由Wolfe线搜索准则计算步长因子，即αk满足(1.11)和(1.12)式.

步3 由(1.2)式计算xk+1，若‖gk+1‖≤ε，停止.

步4 由(1.8)式计算βk+1，(1.9)式计算θk+1，由(1.4)式计算dk+1.

步5k:=k+1，转步2.

引理2.1若假设(H1)和(H2)成立，考虑ZFR1方法，βk和分别由(1.8)式和(1.9)式产生，步长αk满足标准Wolfe线搜索准则，则

证若k=1，d1=-g1，则有

结论成立.对k＞1，假设由(1.12)式易得

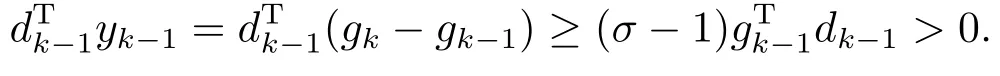
设φk为向量gk与gk－1的夹角，则

若βk＞0，由(1.4)，(1.8)，(1.9)，(1.12)式，并将(1.4)式两端分别与gk作内积可得

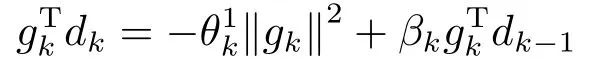
若βk=0，则结合可知

从而，由数学归纳法知，∀k≥10成立，并且得到βk≥0.

引理2.2若假设(H1)和(H2)成立，考虑ZFR1方法，步长αk满足标准Wolfe线搜索准则(1.11)，(1.12)式，则可推出

证引理2.1已证βk≥0，下证不等式右边也成立.

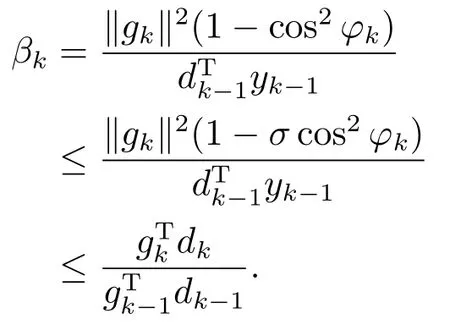
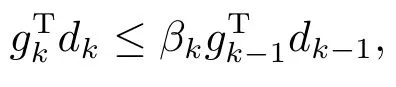
定理2.1若假设(H1)和(H2)成立，考虑ZFR1方法，dk是下降方向，步长αk满足标准Wolfe线搜索准则.则有Zoutendijk条件成立，即

证由引理2.1可知0.

由(1.12)式及假设(H2)，可得

又由于fk为单调递减的收敛数列，再结合上式可得

对上式两端求和得

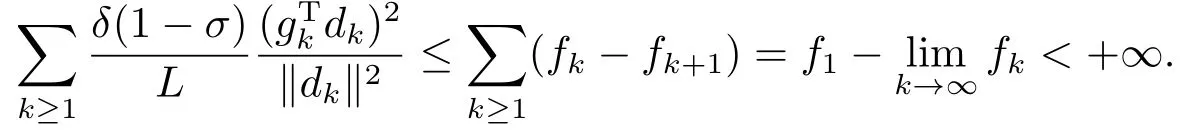
因此，结论成立.

定理2.2若假设(H1)和(H2)成立，考虑ZFR1方法，步长αk满足标准Wolfe线搜索且引理2.1成立，θk是(1.9)式中生成的序列，则

证用反证法证明.若假设(2.5)式不成立.则存在常数r＞0，使得对任意k≥1，有

对(1.4)式移项得dk+θkgk=βkdk－1，两端取模平方并利用(2.3)式可得

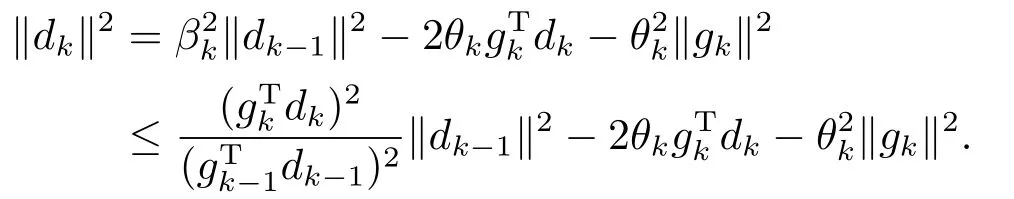
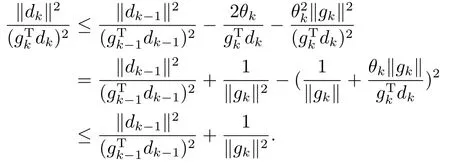
由上式递推，并利用d1=-g1和(2.6)式可得

对上式两端分别求和得

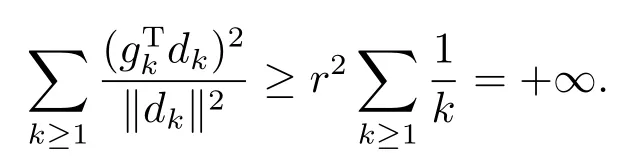
这与定理2.1矛盾，所以定理2.2成立.

3.ZFR2方法及其全局收敛性

算法3.1(ZFR2谱共轭梯度算法)

步1 给定初值x1∈Rn，δ∈(0，)，ε≥0，d1=-g1，k=1;若‖gk‖≤ε，停止;

步2 由Wolfe线搜索准则计算步长因子，即αk满足(1.11)和(1.12)式;

步3 由(1.2)式计算xk+1，若‖gk+1‖≤ε，停止;

步4 由(1.8)式计算βk+1，(1.10)式计算θk+1，由(1.4)式计算dk+1;

步5k:=k+1，转步2.

引理3.1若假设(H1)和(H2)成立，考虑ZFR2方法，βk和分别由(1.8)式和(1.10)式产生，步长αk满足标准Wolfe线搜索，则搜索方向dk满足如下不等式

证若k=1，d1=-g1，则有

结论成立.

对k＞1，假设0，下证0.

由(1.12)式易得

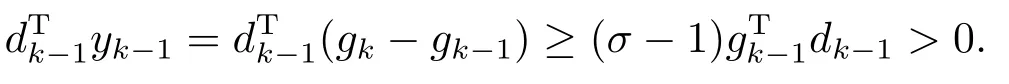
设φk是gk与gk－1的夹角，则cosφk=

1)若βk=0，则由(1.4)式可得

2)若βk＞0，则由(1.4)式可得

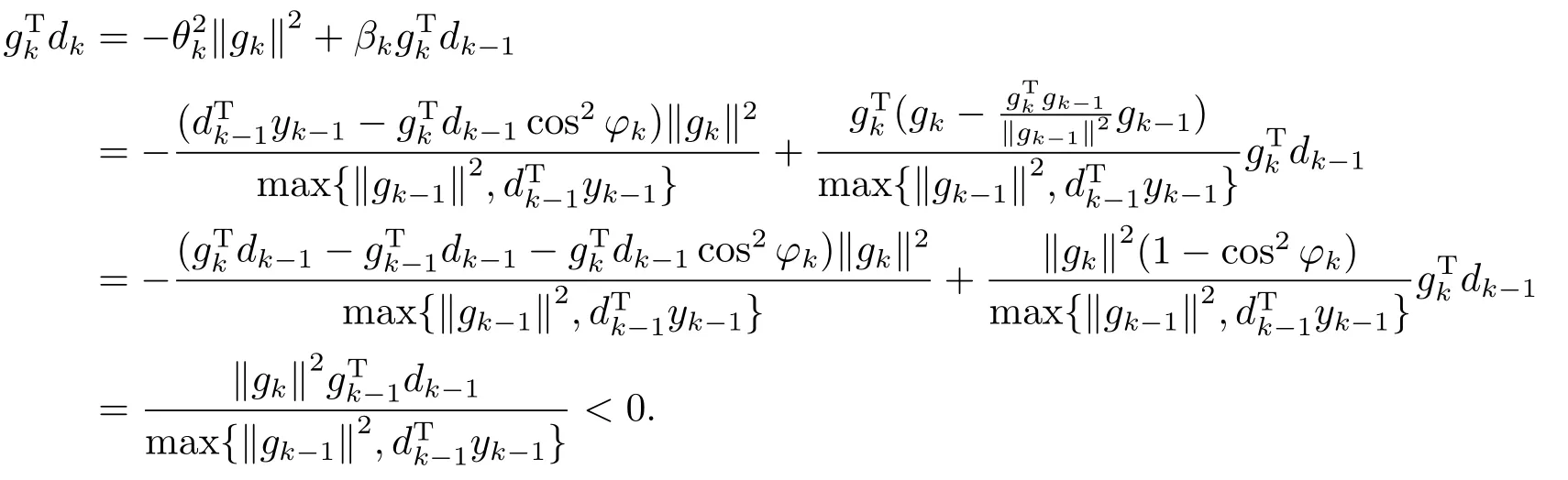
由数学归纳法知引理3.1成立.

定理3.1若假设(H1)和(H2)成立，考虑ZFR2方法，dk是下降方向，步长αk满足标准Wolfe线搜索准则.则有Zoutendijk条件成立，即

由引理3.1、定理3.1和定理2.2，可得以下全局收敛定理成立.

定理3.2若假设(H1)和(H2)成立，考虑ZFR2方法，θk是(1.10)式中的生成的序列，gk由ZFR2方法产生，则

4.数值实验

为检测ZFR1方法和ZFR2方法的数值效果，我们在文[17]中选取了30个大规模无约束优化测试函数的广义或扩展形式.本文用ZFR1方法和ZFR2方法与文[1]中的FR方法、文[2]中的PRP方法、文[16]中的算法1和算法2进行比较，其中文[16]中的算法2用的是Armijo线搜索，其它用的是标准Wolfe线搜索.测试环境为Win10操作系统，Inte(R)Core(TM)i5-8250U CPU 1.60GHz 8.00GB内存.Wolfe线搜索中的参数为:δ=0.01，σ=0.9，ε=10－6，终止条件为‖gk‖≤ε或迭代次数超过10000.Armijo线搜索中的参数为:δ=0.001，ρ=0.8，ε=10－6，终止条件为‖gk‖≤ε或迭代次数超过10000.表1列出了30个函数的名称，N是测试函数编号，function代表测试函数.

表1 测试函数

表2显示了所有数值结果，Dim代表测试函数维数，NI/NF/CPU time分别代表算法迭代次数，目标函数迭代次数和CPU运行时间.“-/-/-”代表存在数值溢出或者该方法在10000次迭代中未能收敛.此外，表2和表3中标记的黑色实验数据是六种方法中测试数据的最小值.

表2 算法的数值结果

同时，我们还采用了Dolan和Mor´e[18]性能图对实验效果进行直观刻画.上面的图1、图2和图3分别对应FR方法、PRP方法、算法1和算法2、ZFR1方法和ZFR2方法在算法迭代次数，函数迭代次数和CPU运行时间比较结果.可以看出，ZFR1方法和ZFR2方法在算法迭代次数、目标函数迭代次数和CPU运行时间等三个指标上均明显优于FR方法、PRP方法、算法1和算法2.

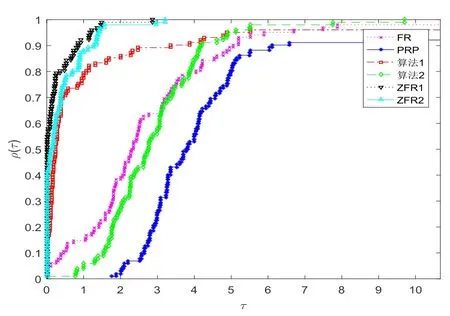
图1 算法迭代次数性能图

图2 目标函数迭代次数性能图

图3 CPU运行时间性能图

5.结果的讨论

首先，从性能图的特征可以知道，曲线越高，相应的方法越好.其次，从上面图1-3、表2和表3可知，ZFR1方法和ZFR2方法成功地解决了100%的测试函数问题，而FR方法、PRP方法和算法1还没有达到100%.ZFR1方法、ZFR2方法在和FR方法、PRP方法、算法1和算法2进行数值比较时，ZFR1方法和ZFR2方法的算法迭代次数、目标函数迭代次数和CPU运行时间都明显减小.因此，可以看出，本文所提出的ZFR1方法和ZFR2方法具有比FR方法、PRP方法、算法1和算法2更好的数值结果.

表3 算法的数值结果

6.结束语

本文在已有共轭梯度算法求解无约束优化问题的基础上，提出了两种新的谱共轭梯度法，并给出了在Wolfe线搜索条件下的全局收敛性证明.数值实验结果表明，本文方法的迭代次数、目标函数迭代次数和CPU运行时间都优于FR方法、PRP方法、算法1和算法2.数值实验验证了这两个方法的有效性.