带有强阻尼项的拟线性抛物方程整体解的存在性与指数增长

吴娇，杨晗

(西南交通大学数学学院，四川成都611756)

1.引言

本文将考虑以下具有强阻尼项的拟线性抛物方程的初边值问题

这里m≥2，p＞2，Ω是Rn(n≥1)中具有光滑边界∂Ω的有界区域.g代表记忆项的核，满足g:R+→R+正的非增函数.该类方程可用于刻画具有记忆功能的热传导材料的数学模型.

当方程(1.1)记忆项缺失时，XU和SU[1]考虑了以下非线性伪抛物方程的初边值问题

得出了整体解的存在性与解在有限时间内的爆破.以上方程整体解的存在性与非存在性主要取决于非线性源项f(u)的增长性，空间维数n，以及初始条件三者之间的相互作用.

当考虑记忆项g0时，问题变得更加复杂，MESSAOUDI[2]研究了如下方程的初边值问题

证明了初始能量为正时解的爆破.并且同作者在文[3]中考虑了含非线性阻尼项的波动方程

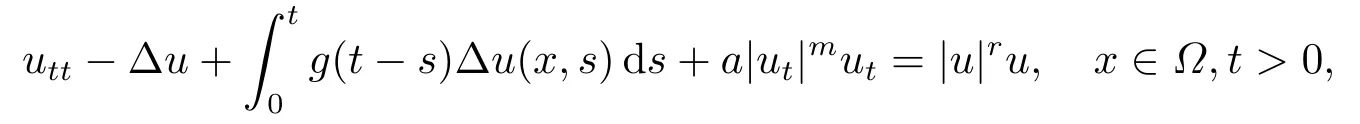
指出当r≤m时，初始值的弱解是整体存在的.当和E(0)＜0时，解在有限时间内发生爆破.而且在06年延伸了E(0)＞0条件下解的爆破结论.LIU等[4]考虑了初边值问题

得出了整体解的存在性和初始值为次能量条件以及任意初始能量条件下解的爆破，并得出了解的生命跨度的上界估计.

对于拟线性情况，PUCCI和SERRIN[5]研究了以下系统

其中m＞1，u∈RN，N≥1.A∈C(J→RN×N)，f∈C(Ω×RN→RN)满足(f(x，u)，u)≥0.当t→∞时证明了强解趋于基态解，无衰减速率.TELLAB和MESSAOUDI[6]考虑了以下方程组

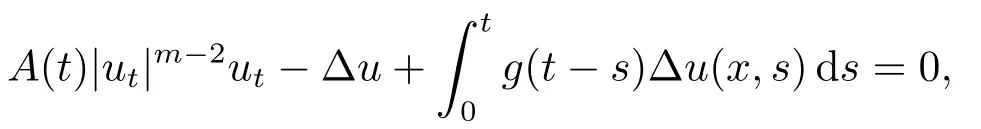
其中m≥2，g满足一般的衰减条件:g′(t)≤-ξ(t)g(t)，建立了解的一般衰减包括指数衰减与多项式衰减.LIU和CHEN[7]证明了带非线性源项的初边值问题

整体解的存在性、衰减估计以及初始能量为正或为负条件下解在有限时刻爆破.

基于以上结论，本文拟研究带强阻尼项的初边值问题(1.1)弱解的存在性、能量衰减和解的指数增长.困难之处在于记忆项、强阻尼项和非线性源项的相互影响.在本文最后一节将看到正是由于强阻尼项的存在，我们无法得到爆破的结论，从而只能得到较弱的一个结果，即解的Lp范数在时间t趋于无穷时至少以指数形式增长.

本文安排如下，在第二部分将提出一些假设与记号，在第三部分利用Galerkin方法得到局部解的存在性.第四部分得整体解的存在性与能量衰减估计，最后证明解的指数增长.

2.准备工作

首先给出证明过程中的所需假设、记号和引理.对松弛函数g和非线性项指数m，p假设如下

(G1)函数g:R+→R+是可微函数满足

(G2)存在非增可微函数ξ:R+→R+满足

(G3)假设

注2.1有很多满足假设(G1)和(G2)的函数，对于合适的a，b＞0，

拟引入以下的能量泛函:

其中

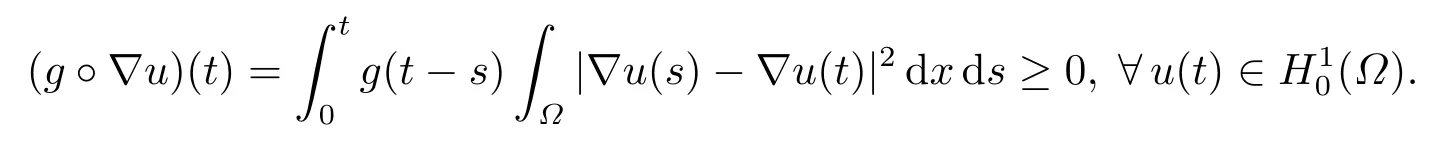
为了叙述主要的结论，我们给出方程(1.1)弱解的定义.

定义2.1方程(1.1)的弱解是函数

满足

以上式中t∈[0，T]和(Ω).

引理2.1设u(t)是方程(1.1)的解，则E(t)在[0，T]中是非增函数且满足

对几乎处处的t∈[0，T]成立.

证在方程(1.1)两边乘ut并在Ω上积分，由(G2)和分部积分得形如(2.2)在中的正则解.再由函数空间在的稠密性得上述结论.

在正式给出结论之前，借助文[7]，首先给出以下的记号

其中C*是(Ω)(Ω)的最佳Sobolev嵌入常数.定义函数γ(t)为

从E(t)的定义和得

由微积分知识得G在0≤λ＜λ1上单调递增，在λ＞λ1上单调递减.当λ→+∞时，G(λ)→-∞并且

其中λ1和E1在(2.3)中已给出.

引理2.2[7]假设0≤E(0)＜E1.

(i)如果‖∇u0‖2＜λ1，则存在使得t∈[0，T);

(ii)如果‖∇u0‖2＞λ1，则存在λ2∈(λ1，+∞)使得t∈[0，T)且有‖u‖p≥Bλ2.

引理2.2在本文证明解的指数增长中起着重要的作用.

3.局部解的存在性

首先给出局部弱解的存在性的定理.

定理3.1假设(G1)，(G2)和u0∈成立，2＜m满足(G3)，则方程(1.1)存在弱解u(x，t)满足u(x，0)=u0和

证将利用Galerkin方法证明，证明过程分为三步.

定义有限空间Vl=span{ω1，ω2，...，ωl}，固定正整数l.记u0l是Vl的元素，使得当l→∞时

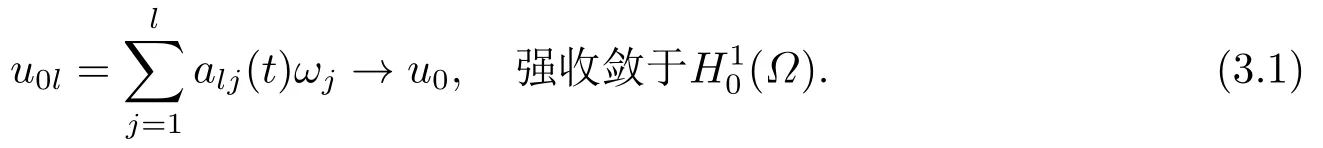
记问题(1.1)的近似解为ul(x，t)且

这里的系数αlj(1≤j≤l)满足常微分方程

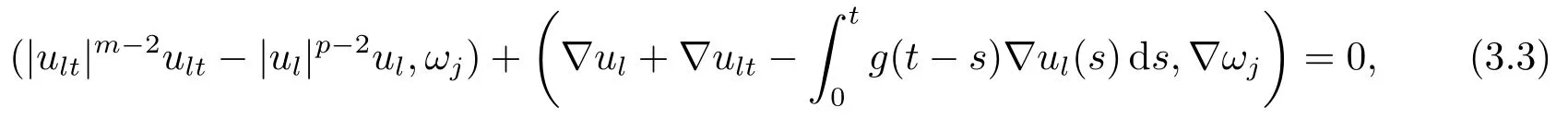
其中j∈{1，2，...，l}和初始条件

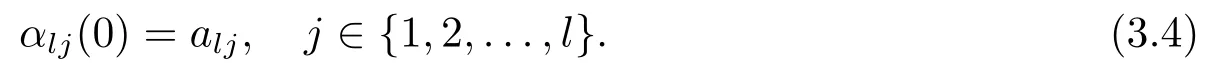
由常微分方程的理论知存在正数T1使得αlj∈C1[0，T1)，所以

步2先验估计.在方程(3.3)两边乘αlj(t)，并对j=1，...，l求和得

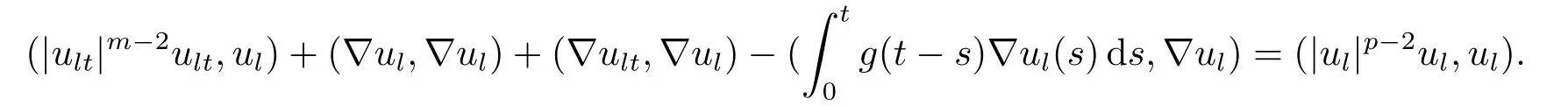
则

方程两边对时间t在[0，t]上积分，令

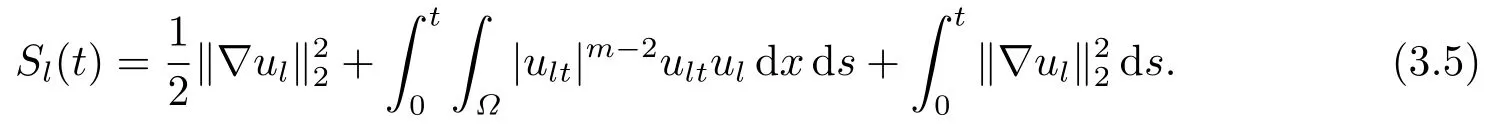
则

利用G-N不等式，Young不等式，嵌入定理和(3.5)，估计(3.6)右边第三项得

其中ε∈(0，1)和

这里C1和C2均为独立于l的正常数.由Gronwall-Bellman-Bihari的积分类型不等式知，存在正的常数使得

最后对任意的l，(3.3)式的解在[0，T]上存在.

其中

由函数E(t)的连续性和(3.1)知存在正的常数C(独立于n和T)使得

所以由(3.11)知

从(3.5)和(3.10)得

步3取极限.结合(3.11)-(3.14)知，存在函数u和的子序列仍记为使得

下面证明非线性项的收敛性.从(3.15)，(3.16)和Aubin-Lions-Simon引理知

所以ul→ua.e.(x，t)∈Ω×(0，T).这表明

另一方面，由(3.14)和Sobolev不等式得

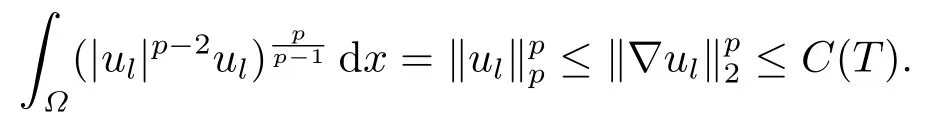
因此通过Lions引理和(3.18)有

对|ut|m－2ut利用Sobolev紧嵌入定理并结合(G3)同理知

以及

因此

即方程(1.1)的解u存在且在中满足初始条件u(x，0)=u0(x)和

对任意的ω和几乎所有的t∈[0，T]成立.所以方程(1.1)存在局部解.

4.整体解的存在性和能量衰减估计

引入以下函数:

定理4.1假设0＜‖∇u0‖2＜λ1，0＜E(0)＜E1和(G1)-(G3)成立，则方程(1.1)的弱解u(x，t)整体存在，且有如下的衰减估计

其中K和ω为正的常数.

借助文[7]的方法，首先证明整体解的存在性.

证定义修正的能量泛函

由(G1)，(G2)和引理2.2知

所以

而且由(2.1)，(4.1)得

由引理2.1知E(t)≤E(0).另一方面由(G1)，(G2)知

由引理2.2和上式得

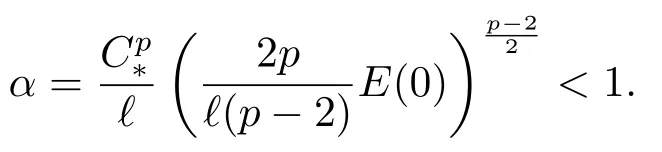
由E(t)的定义得

由ϵ(t)的定义和(4.2)-(4.4)知

即

其中Γ只与p有关.由以上估计和连续性原理可知全局解存在.

在证明衰减估计之前，首先给出相应的引理.

引理4.1[8]令E:R+→R+是非增函数，φ:R+→R+是二阶连续可导的单调递增函数满足φ(0)=0和假设存在常数c＞0使得

则

其中λ和ω为不依赖于E(0)的正常数.

定理4.1的证明在方程(1.1)两边乘ξ(t)u并且在Ω×(S，T)上积分得

估计等式左边的最后一项

从(2.1)和(4.6)得

结合(2.1)，(2.2)，(4.2)和(G3)得

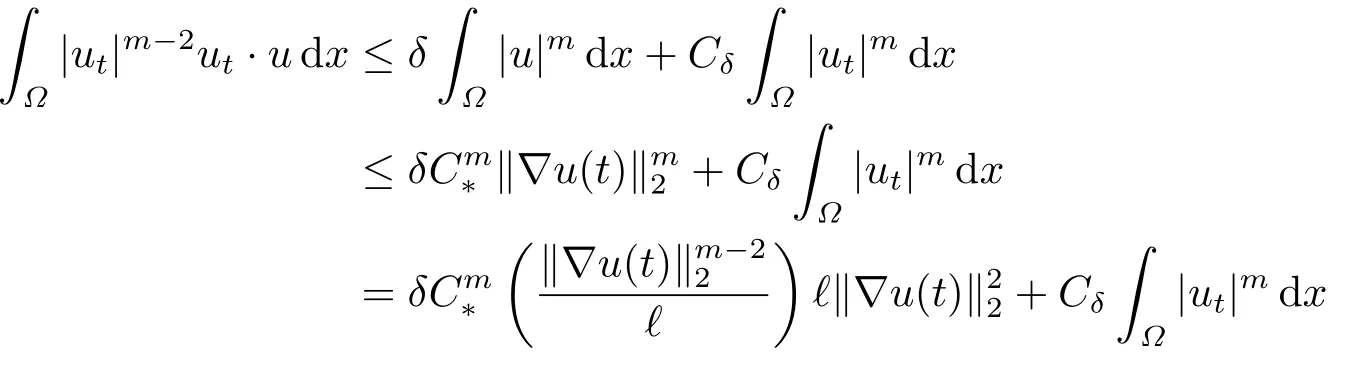
由Young不等式，(2.2)，(4.2)得

结合(G2)和(2.2)知

因此由(4.3)，(4.9)-(4.12)得

由整体解的证明知α＜1，选取δ足够小使得

即存在正常数δ＞0使得

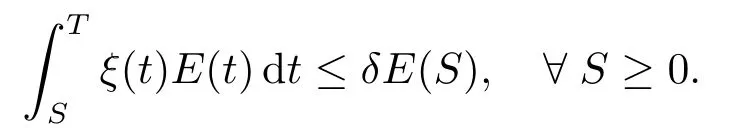
在不等式左边通过令T→∞，当ds时满足(4.5)，所以结论成立.在定理4.1的证明中，我们没有限制非线性项指数m，p的大小关系，但要求初始条件u0满足0＜‖∇u0‖2＜λ1，0＜E(0)＜E1.下面我们将去掉这一限制条件，在m≥p这一条件下，证明如下的整体解存在的结论，即表明阻尼强于源时，整体解一定存在.

定理4.2假设和m≥p成立.则对任意T＞0，方程(1.1)存在弱解.

证定义修正的能量泛函

通过方程(1.1)和(2.2)得

由Young不等式和m≥p可知

此时存在两种情况：当‖ut‖m＞1时，选取ε足够小使得

即

从以上估计和连续性原理知定理成立.

5.指数增长

拟证明问题(1.1)的能量是无界的.事实上，将证明问题(1.1)在初始能量为负或初始能量有一临界的正的下界，且时间趋于无穷时，解的Lp范数将以指数函数增长趋于无穷.

定理5.1假设成立且满足下列条件之一

(i)E(0)＜0;

(ii)‖∇u0‖2＞λ1，0＜E(0)＜E2=其中2＜q＜p，u(x，t)是方程(1.1)-(1.3)的局部解.而且假设

则该方程解的Lp范数将以指数形式增长.

证令

结合(2.2)和(5.2)得

所以

且

在方程(1.1)两边乘u，在Ω上积分并对(∇ut，∇u)使用Young不等式得

对某些δ使得其中

由引理2.2(ii)和E2的定义知

所以从上式和(5.4)得微分不等式

对(5.10)在0和t之间积分得H的以下估计

另一方面，又由H的定义知

结合(5.10)，(5.11)得解的Lp范数将以指数形式增长.

对于E(0)＜0，在(5.2)中令H(t)=-E(t)，证明过程大致同上，在此省略.

注5.1提出证明方程(1.1)在有限时间内爆破的困难之处:1)添加了强阻尼项Δut后，在方程中乘u并对此项利用Young不等式放缩时，关于H函数(同定理5.1)得H′≤H1+θ，θ＞0;2)定义辅助函数且由方程中指数决定.在对估计时，因无法用L′(t)中函数控制，所以不成立;3)利用微分不等式技巧建立两个辅助函数间的关系(类似文[1]利用凸方法构造辅助函数M(t))证明在负初始条件下解的爆破时，不能建立M(t)M′′(t)与M′(t)的关系;4)若已知E(0)＜0下解的爆破，且设初始条件满足M与m，p有关，可证明在任意初始能量下解在有限时间内爆破.

注5.2DI[9]证明有限时间内的爆破中通过对高阶项利用格林公式去掉了文中(5.5)的项(本文证明有限时刻内爆破困难的主要影响项)，并利用不等式放缩得到关于H(t)的微分不等式H′(t)≥ξH(t)1+α对某些α＞0，进而得到解的爆破，而本文只能得到估计H′(t)≥ξH(t)，从而得到解的Lp范数以指数函数增长.