一种基于内外环结构的四旋翼飞行器的PD控制方法

王振,庞爱民,马双宝

(武汉纺织大学 机械工程与自动化学院，湖北 武汉，430200)

四旋翼飞行器是当今控制工程研究中的热门领域，由于其可以进行垂直升降，并且具有结构简单化、飞行姿态多样化、飞行噪声小等特点，其在军工和民用领域都有着广泛的应用，如应用在抗洪抢险、高压电路巡检设备、高空航拍和汽车导航等方面。具有轻量化特点的四旋翼飞行器在高空飞行过程中，机身四周顶部的螺旋桨在电机带动下高速旋转，容易在外部扰动作用下出现机身抖动的情况，系统控制可靠性能大大降低。本文主要研究四旋翼飞行器在飞行过程中的系统稳定跟踪控制问题。文献[1]考虑电机出现故障的 3 种不同情形下，结合积分反演控制技术和时延控制(TDC)技术对上一个系统状态进行迭代，进而逼近和补偿四旋翼无人机执行机构的故障信息；文献[2]提出传统PID控制适用于线性系统类型的工程应用，其控制参数固定不变，很难适应四旋翼的灵活性。文献[3]提出模糊控制，可以解决PID控制在非线性控制中抗干扰能力弱的问题，模糊控制作为一种先进控制策略可以在非线性系统中取得较好的控制效果。文献[4]提出了一种基于状态观测器技术的故障诊断方法，并对其鲁棒性与快速性进行了理论分析。文献[5]根据四旋翼飞行器系统动力学模型，控制四旋翼飞行器的位姿。文献[6-7]改进传统无迹卡尔曼滤波算法，结合陀螺仪漂移误差模型，使用四元数的方法构造无迹卡尔曼滤波状态方程，有效减小了非重力加速度对姿态解算的影响。文献[8]提出一种四旋翼飞行器的滑模控制方法，实现了飞行器的稳定跟踪问题。针对上述问题，文献[9]中的方法并对其改进，提出以四旋翼飞行器位置子系统作为外环，姿态子系统作为内环。分别在外环角度和内环角速度控制器中加入PD控制器的方法，从而实现对四旋翼飞行器的稳定姿态跟踪控制。

1 四旋翼飞行器的动力学模型

四旋翼飞行器通过机身四周顶端4个旋翼旋转产生向上的升力，使其在空中飞行。飞行的位姿可由4个旋翼的转速控制。四旋翼飞行器具有6个自由度，但在实际飞行过程中，不需要对6个自由度进行跟踪。本文选用的控制目标方法为：对飞行轨迹[x,y,z]和横滚角φ进行跟踪控制，同时确保俯仰角θ和偏航角ψ镇定。其简化结构图见图1。根据拉格朗日方程，其动力学方程可以描述如下[10-11]：

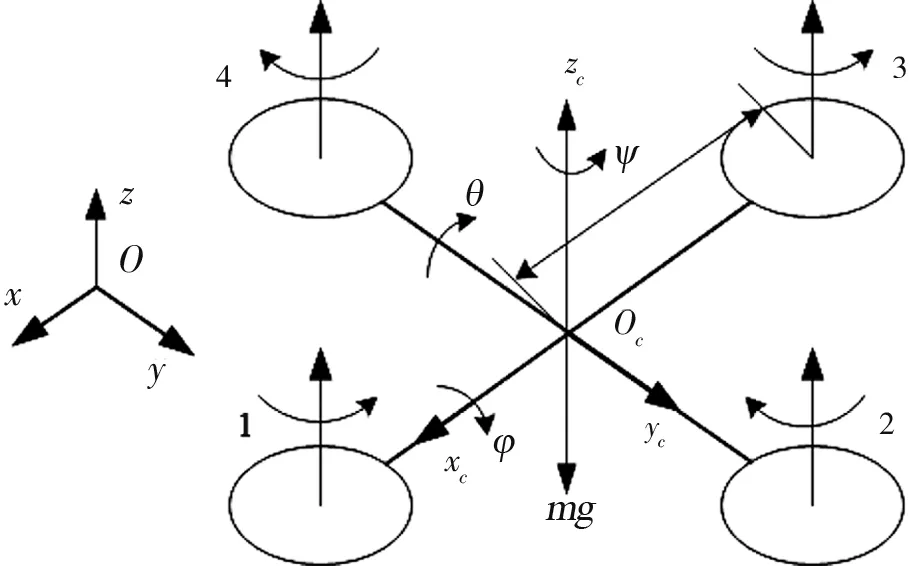
图1 四旋翼飞行器结构图Fig.1 Geometric diagram of a quadrotor

(1)

式中:[φ，θ，ψ]为飞行器在世界坐标系下的欧拉角；[x,y,z]为飞行器质心在世界坐标系中的位置；m为飞行器的质量；Ii为每个轴的转动惯量；Ki为阻力系数；l为旋翼到飞行器重心的长度。

2 位姿控制律设计

针对四旋翼飞行器的二阶控制系统，根据Hurwitz判据，二阶系统a2s2+a1s+a0=0的稳定性条件是：

(2)

通过设计系统位置控制律来实现x→0,y→0,z→zd，可设计位置控制律为u1。通过式(1)定义：

(3)

则位置状态模型可简化为

(4)

PID控制器通过给定值和实际输出值构成采样偏差，由采样偏差来调整实时控制量。本文中，为使系统调节过程迅速，选用PD控制器。

首先，采用PD控制方法设计x轴位置子系统的设计控制律为

(5)

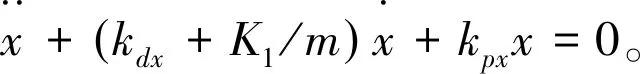
kpx>0,kdx+K1/m>0

同理，y轴位置子系统设计PD控制律为

(6)

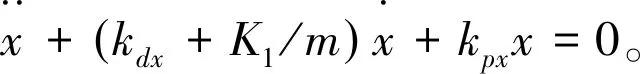
集中集热分户储热太阳能热水系统现场总线控制应用分析……………………………………… 刘玮，尹立增，郭卫星（3-46）

kpy>0,kdy+K2/m>0

z轴位置子系统设计PD控制律为

(7)

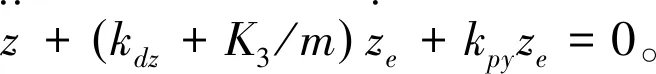
kpz>0,kdz+K3/m>0

假设θd,ψd满足控制律式(5)～式(7)时，为实现θ→θd，ψ→ψd，因此，必须求解θd和ψd。

由(3)式可得：

(8)

(9)

则位置控制律为

(10)

由姿态控制律实现θ→θd,ψ→ψd,φ→φd。

(11)

首先，针对俯仰角子系统取θe=θ-θd，采用前馈补偿PD控制方法，设计控制律为

(12)

同理，偏航角子系统设计控制律为

(13)

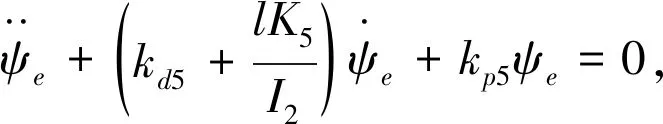
第三个姿态角子系统设计控制律为

(14)

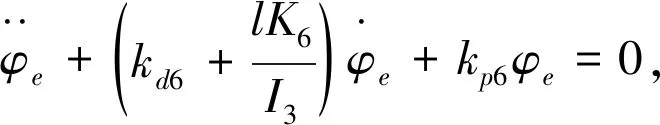
在本系统中，根据Hurwitz判据，二阶系统稳定性条件只需满足比例系数和微分系数均大于0，即可保证x,y和z轴位置子系统及θ，φ和ψ角度子系统的稳定性。

3 系统闭环控制模型

由于传统的PID控制对仅考虑了四旋翼飞行器系统的飞行角度，这样得到的结果使系统的鲁棒性差，稍有扰动便可能导致系统不稳定，故本文采用内外环结构PD控制对飞行器的位姿进行控制，控制框图见图2。

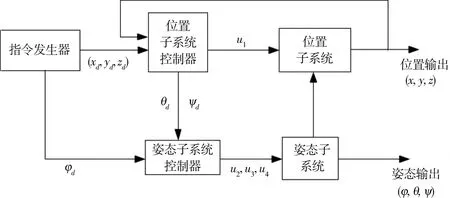
图2 四旋翼飞行器控制结构图Fig.2 Control structure diagram of a quadrotor

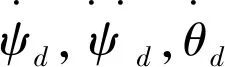
(15)

其中：待微分的输入信号为v(t)；ε=0.04；x1为对信号进行跟踪；x2为信号一阶导数的估计；x3为信号的二阶导数的估计。微分器的初始值为x1(0)=0,x2(0)=0,x3(0)=0。

由于微分器可对非连续函数求导，因此，不要求指令信号ψd和θd连续，从而位置控制中可以有切换函数。该微分器具有积分链式结构，在对含有噪声的信号求导时，噪声只含在微分器的最后一层，通过积分作用信号一阶导数中的噪声能够被充分抑制。在内外环控制中，内环的动态性能影响外环的稳定性，进而影响整个闭环控制系统的稳定性。为实现收敛速度快的内环控制，采用内环收敛速度大于外环收敛速度的方法来保证闭环系统的稳定性。在本算法中通过调整内环控制其增益系数，即在姿态控制律的设计中，为了使内环较外环收敛速度快，采用较大的PD增益，保证内环收敛速度大于外环收敛速度。

4 仿真结果

根据四旋翼飞行器的动力学模型及闭环系统结构框图，在MATLAB环境下编程对上述系统控制方法进行相应的仿真试验。仿真试验选用四旋翼飞行器的相关参数见表1。

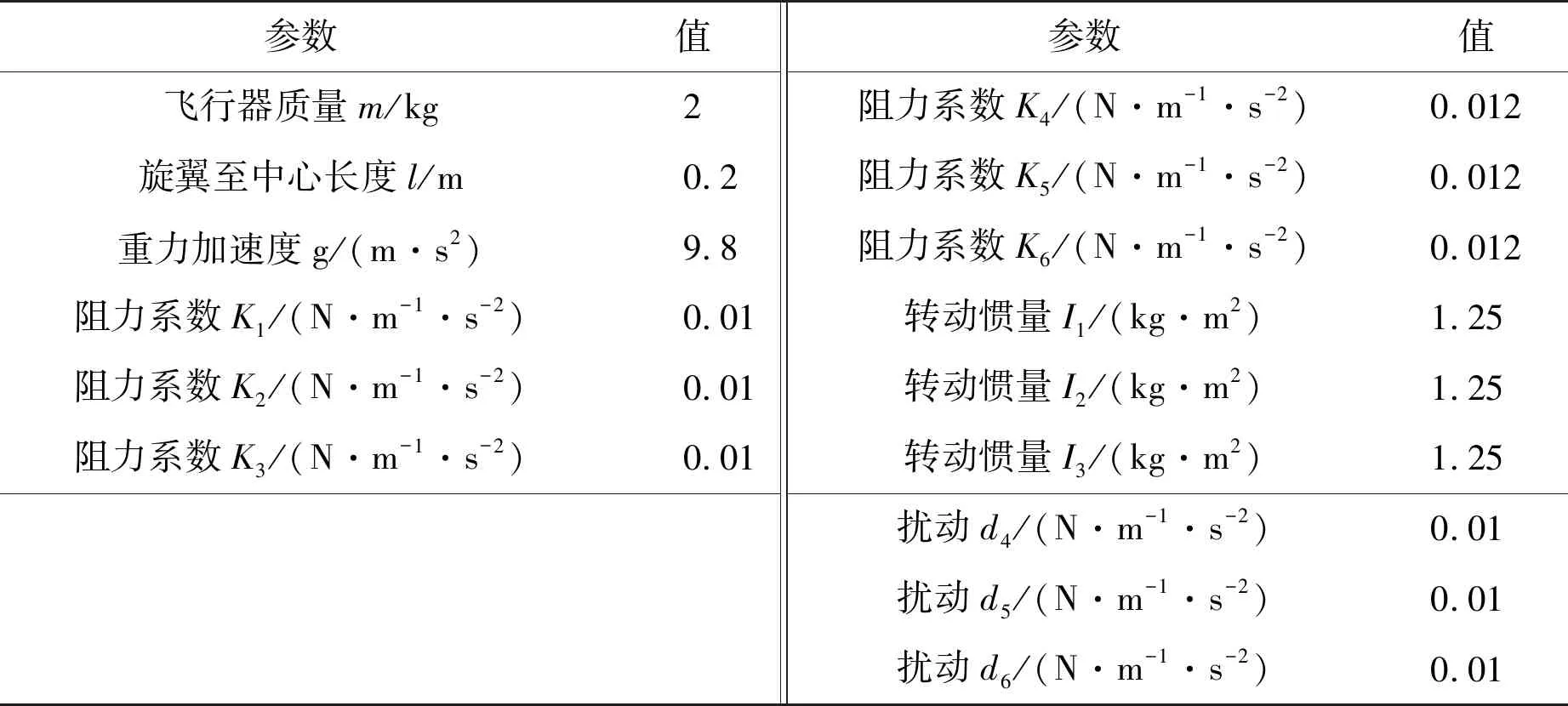
表1 系统结构参数表

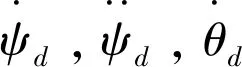
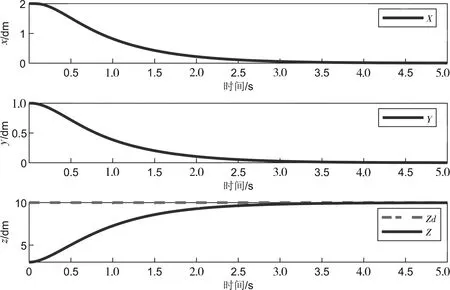
图3 位置状态收敛过程Fig.3 Convergence process of position state

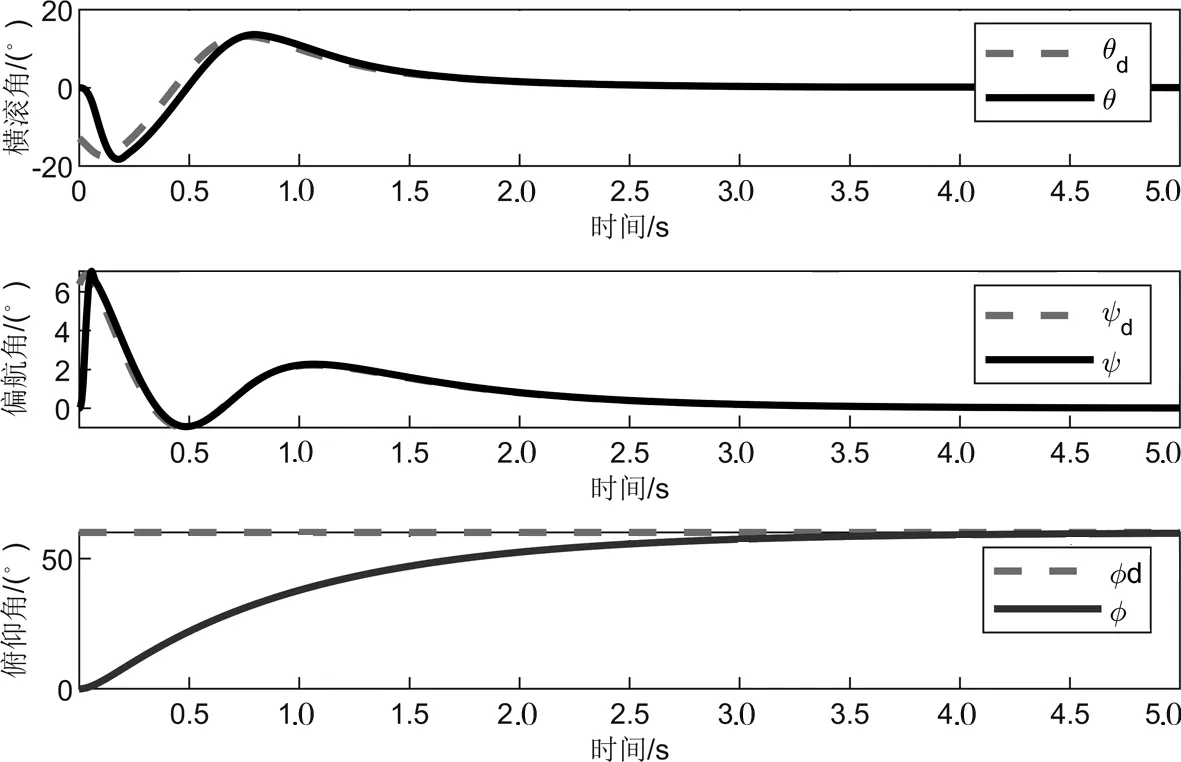
图4 姿态收敛过程Fig.4 Convergence process of posture

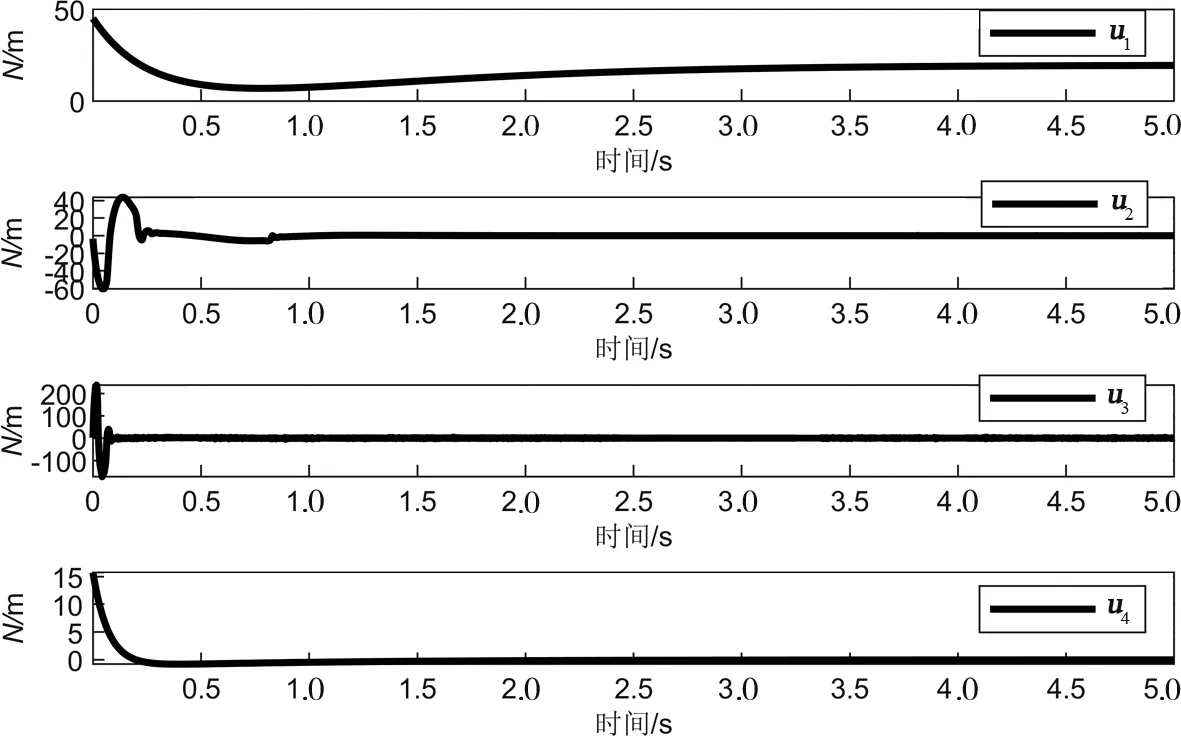
图5 4个控制输入变化过程Fig.5 Four variation processes of control input

5 结论

在控制过程中，系统动力学方程经过解耦工作，简化了计算机计算时间，同时有效地避免了控制参数相互影响，使每个参数在控制过程中独立控制，避免出现大的超调，系统可以稳定悬停于空中。引入PD控制器，在比例控制微分控制参数作用下能够快速反应，在x，y和z3轴的位置调节过程中，很快达到控制要求，并且实现稳定悬停。