基于智能算法的平整延伸率系统辨识与控制

任新意，高慧敏，黄华贵，王晓东，孙静娜

(1.首钢京唐钢铁联合有限责任公司技术中心，河北 唐山 063200； 2.燕山大学国家冷轧板带装备及工艺工程技术研究中心，河北 秦皇岛 066004)

0 前言

在冷轧工艺中，连续退火生产线的平整技术是保证最终产品性能和表面质量的关键工序[1-3]。平整机最重要的工艺控制为带钢的延伸率控制，用于消除冷轧带钢的浪形、翘曲等板形缺陷，提高产品的质量品质和改善带钢的力学性能[4]。

平整延伸率控制系统是典型双环控制系统[5-7]，其中轧制力控制为内环控制系统，延伸率控制为外环控制系统。它将延伸率调节器的输出作为轧制力附加给定值，通过改变轧制力对延伸率进行闭环控制，从而消除各种因素的变化对延伸率控制的影响。平整延伸率控制系统具有电液耦合特性、参数时变特性、外界干扰和非线性等情况[8]，所以常规控制手段很难获得满意的效果。

本文以某2230连退生产线平整机组为研究对象[9]，综合考虑各组成部件的动态特性的基础上，建立平整机延伸率控制系统的机理模型，并采用BP神经网络对控制系统进行参数辨识，提高模型的设定精度。此外，结合免疫系统调节规律和模糊推理算法，利用模糊免疫PID控制策略对平整延伸率系统进行控制，提高平整延伸率系统的控制精度以及存在外界干扰和模型失配条件下的调控能力。

1 平整机延伸率控制系统模型

平整机组是延伸率控制的执行机构，主要由液压压下子系统、张力协调子系统等组成。平整机延伸率模型液压压下子系统主要由压力控制器、伺服放大器、伺服阀、油压负载等组成，张力控制子系统由自动张力控制器、电流控制器、整流电路、前后张力辊组等组成[10]。平整机延伸率控制系统框图如图1所示。

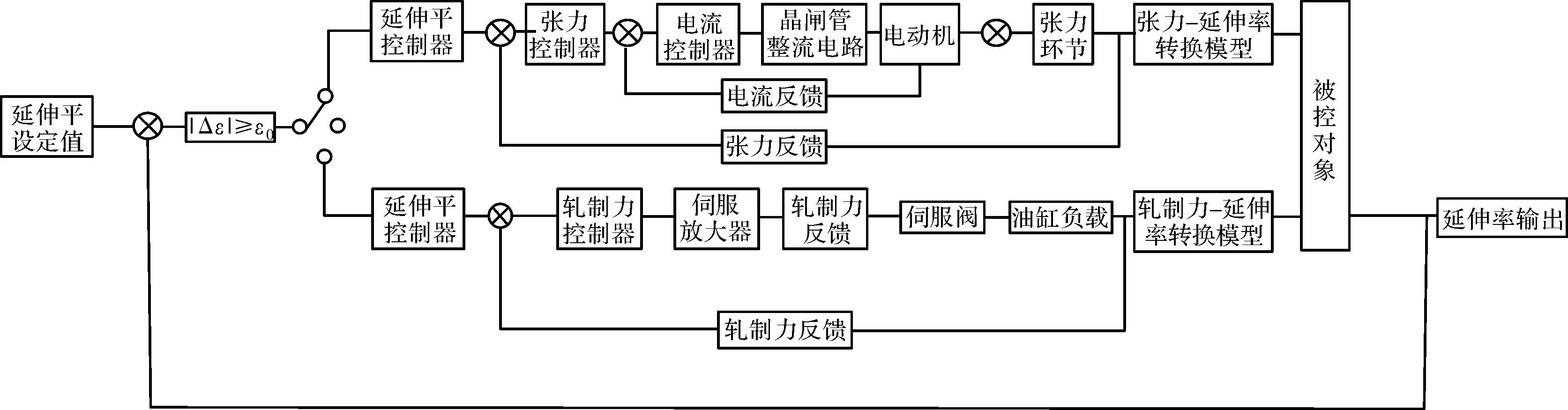
图1 平整延伸率控制系统框图

平整机延伸率控制系统轧制力模式是基于延伸率反馈的轧制压力控制系统[11]，该系统通过调节轧制力对延伸率进行控制，平整机延伸率轧制力数学模型如图2所示，包括伺服放大器，伺服阀，油缸负载和轧制力-延伸率转换关系。

图2 平整机延伸率系统轧制力数学模型

在不影响系统特性的基础上将平整机的辊系考虑为单自由度的质量弹簧系统[12]，可将压力传感器视为比例环节，则其传递函数模型

(1)

式中，k=kfkqkaksvAp/kce。将其离散化，则模型可描述为

(2)

式中，ai、bi为离散模型各项系数。

2 基于BP神经网络的延伸率控制系统辨识

BP神经网络是通过误差逆向传播算法进行误差校正的多层前馈神经网络[13]，由输入层、中间层和输出层组成，各层之间采用全互联方式，且同一层单元之间不存在相互连接，各层之间的连接权值可以通过学习来调整，能够实现数据压缩、模式识别、参数辨识和函数逼近等功能[14-16]。综合考虑平整机延伸率控制系统的非线性、时变和时滞等特性，基于平整机延伸率的机理模型，通过BP神经网络辨识式中的增益系数，从而提高模型的精度。平整机延伸率辨识系统的结构如图3所示。

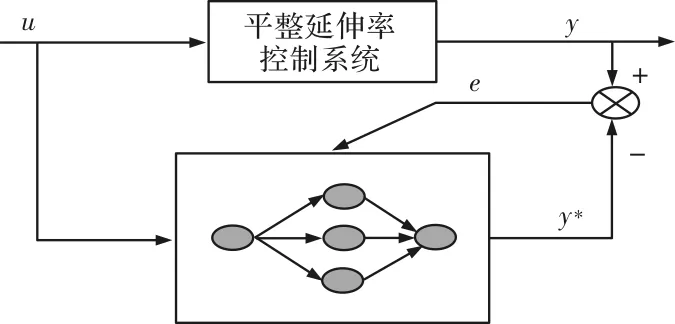
图3 平整机延伸率控制系统辨识模型

采集现场实际生产数据平整轧制力的设定值和实测值，选取每组数据中的轧制力阶跃数据作为辨识数据，并对数据进行预处理，得到平稳、正态、零均值的时间序列，如图4所示。

图4 平整轧制力原始数据及处理后数据

利用MATLAB神经网络辨识工具箱[17]辨识出离散模型的各项参数，其拟合度为94.47%。基于神经网络的离散化辨识模型为

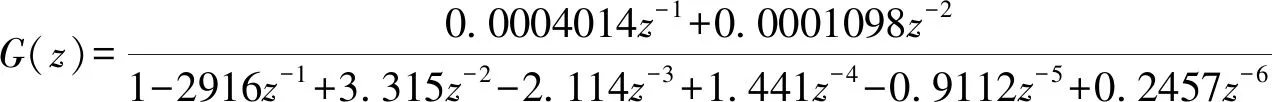
(3)

从现场采集的数据中再随机抽取一组数据，取其平整轧制力设定值作为辨识模型仿真的输入，将辨识模型的仿真输出与系统实际输出对比，验证所辨识模型的可靠性，如图5所示。

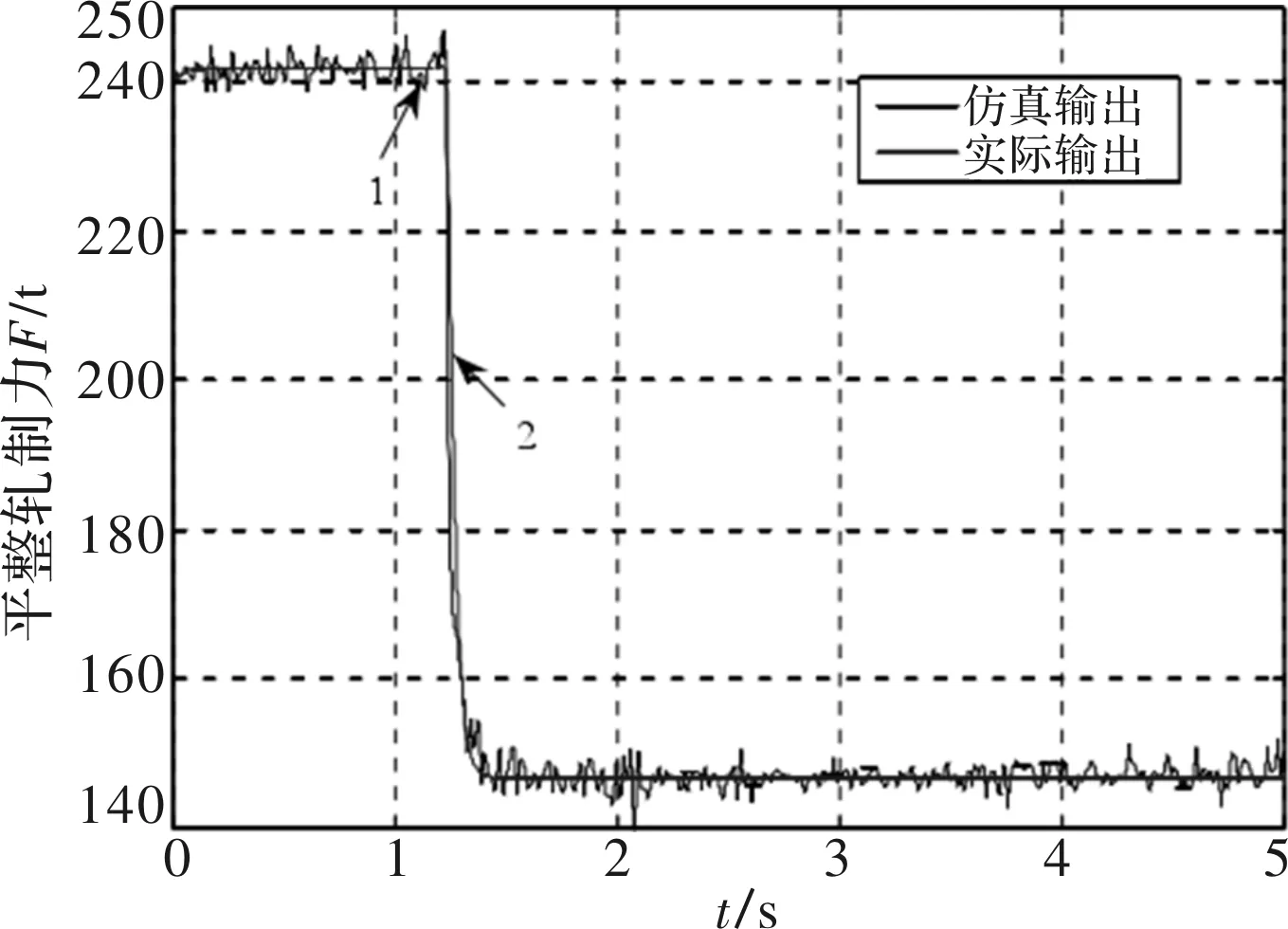
图5 平整延伸率辨识模型跟随情况

辨识模型仿真输出能很好的与系统的实际响应拟合，辨识模型的仿真输出与实际系统的响应误差较小，因此，可以认为辨识结果准确可信。

3 模糊免疫PID控制器设计

3.1 免疫算法原理

人工免疫系统是在生物免疫系统的启发下，通过模拟其对外界物质的自然防御机理，实现噪声忍耐、自学习、自组织和记忆等功能，适合于解决具有鲁棒性、自适应和动态要求的实际工程应用问题[18]。

由于抗原的入侵，B细胞一方面受到TH细胞(辅助细胞)的活化作用；另外一方面也接受TS细胞(抑制细胞)的抑制作用。这样第k代B细胞的浓度可以这样表示

B(k)=TH(k)-TS(k)=K1ε(k)-K2{[ΔB(k-d)]}ε(k)

(4)

式中，ε(k)为第k代抗原浓度；K1为TH细胞的促进因子，K2为TS细胞的抑制因子；ΔB(k)为B细胞的浓度变化。f(·)为一非线性函数，表示在第(k-d)代时，B细胞分泌的抗体与抗原相互作用的免疫效果。

由(4)式可得到B细胞浓度与抗原浓度关系式

B(k)=K{1-ηf[ΔB(k-d)]}ε(k)

(5)

以B细胞浓度B(k)作为控制器的输出u(k)，抗原浓度ε(k)作为偏差e(k)，则可以得到免疫控制器

u(k)=KP1e(k)KP1=K{1-ηf[u(k),Δu(k)]}

(6)

式中，K=K1,η=K2/K1，表示TS与TH作用的比例系数。K和η是两个重要参数，K增大会提高响应速度，而η增大会减小系统的超调量，合理地调整这两个参数，即可使控制系统具有较快的响应速度和较小的超调量[19]。

3.2 模糊推理算法

利用模糊控制器良好的逼近性[20]，采用一个模糊控制器来实现非线性函数f(·)。用免疫控制器的输出u(k)和输出变化量Δu(k)作为模糊控制器的输入，用非线性函数f(·)作为模糊控制器的输出。

每个输入变量被两个模糊集模糊化，分别是“正”(P)和“负”(N);输出变量被三个模糊集模糊化，分别是“正”(P)、“零”(Z)和“负”(N)。隶属度函数都定义在整个(-∞,+ ∞)区间。按照“细胞接受刺激越大，则抑制能力越小”及“细胞接受的刺激越小，则抑制能力越大”的原则，可采用四条模糊规则

(1) IfuisPand ΔuisPthenf(u,Δu) isN(1);

(2) IfuisPand ΔuisNthenf(u,Δu) isZ(1);

(3) IfuisNand ΔuisPthenf(u,Δu) isZ(1);

(4) IfuisNand ΔuisNthenf(u,Δu) isP(1)。

其输入隶属度函数如图6所示，输出隶属度函数如图7所示。

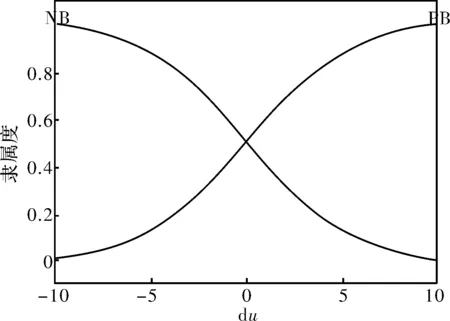
图6 免疫PID控制u、du隶属函数

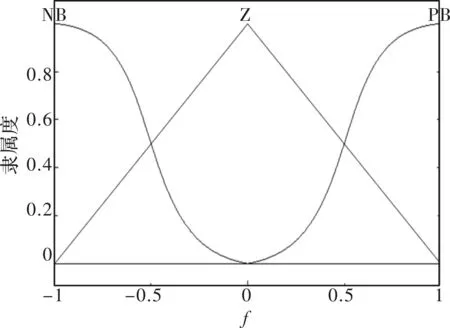
图7 免疫PID控制f(·)隶属函数

各规则中，使用Zadeh的模糊逻辑AND和OR操作，并采用“centroid”反模糊化方法得到模糊控制器的输出f(·)。

则模糊控制在线调整积分系数与微分系数的表达式为

KI1=KI0+ΔKI

(7)

KD1=KD0+ΔKD

(8)

3.3 模糊免疫PID控制器

以常规PID算法为基础，结合免疫算法和模糊推理算法，从而可以得到模糊免疫PID控制器算法。模糊免疫PID控制器结构如图8所示。

图8 模糊免疫PID控制原理

常规的PID控制算法的离散形式为

(9)

则模糊免疫PID控制算法的离散形式为

(10)

4 仿真结果分析

根据本文建立的某2230连退平整机延伸率控制辨识系统模型，分别采用常规PID、模糊PID和模糊免疫PID等三种方法，测试在阶跃响应条件下的系统调控性能。同时，在第100 s加入单位阶跃扰动信号，测试系统的抗干扰性能，所得到的仿真曲线如图9和图10所示。

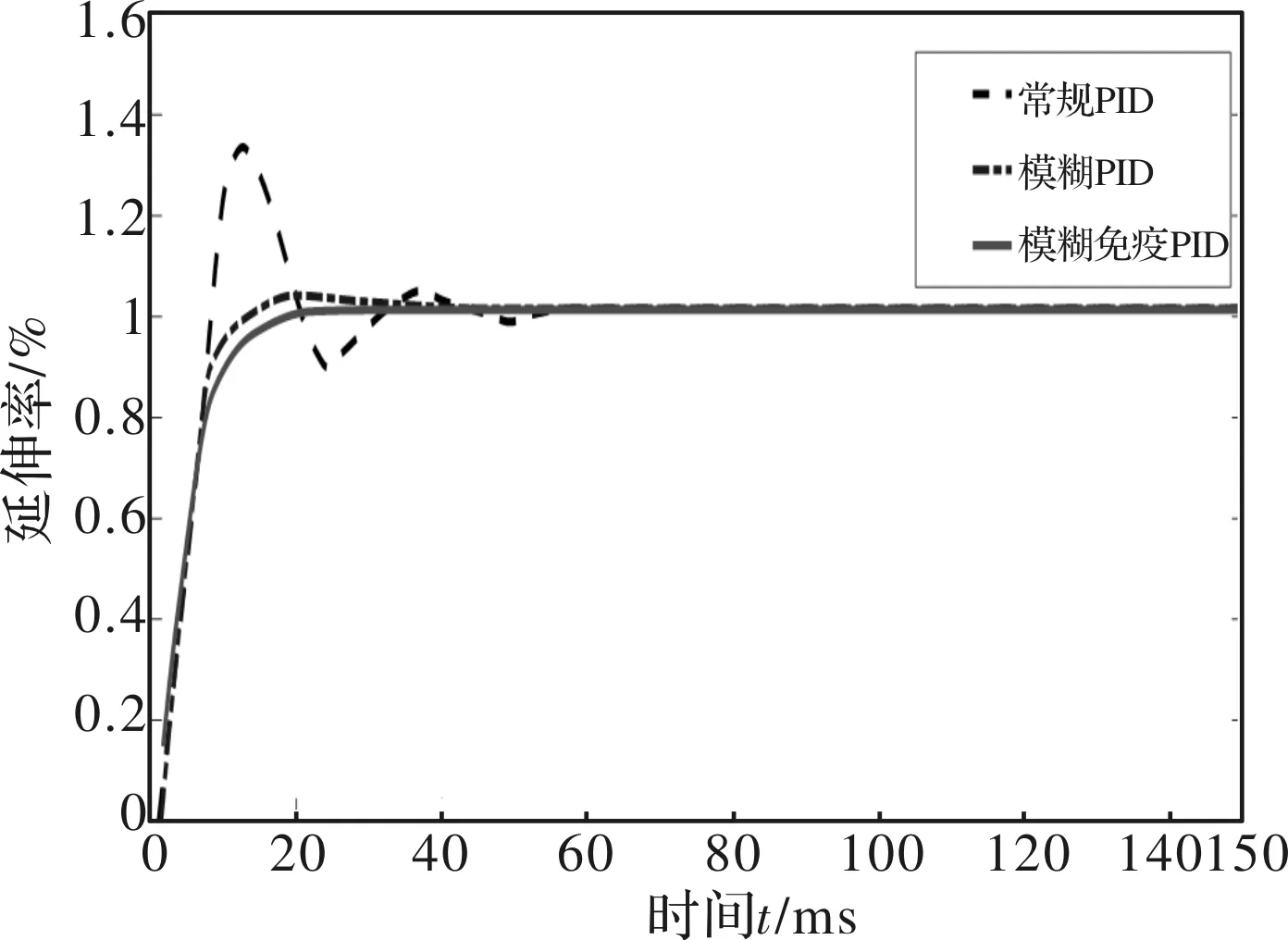
图9 平整延伸率控制系统阶跃响应对比曲线

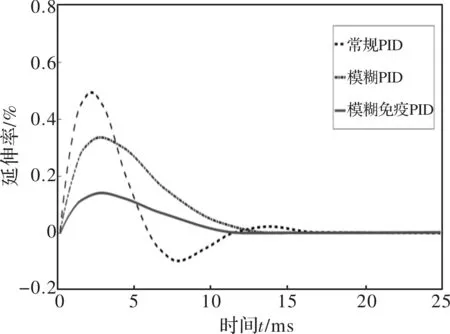
图10 不同控制策略的抗干扰能力对比曲线

由仿真对比结果可知，常规PID反馈控制系统的超调量很大，而且过渡时间很长。而基于模糊免疫PID的控制系统不仅可以实现无超调，而且响应速度快，过渡过程时间短，且具有较强的抗干扰能力。

为了进一步测试控制系统在存在大时滞以及模型参数失配情况下的控制性能，在原有平整机延伸率控制系统中增加12 s的延迟时间，并改变模型参数，仿真对比结果如图11所示。

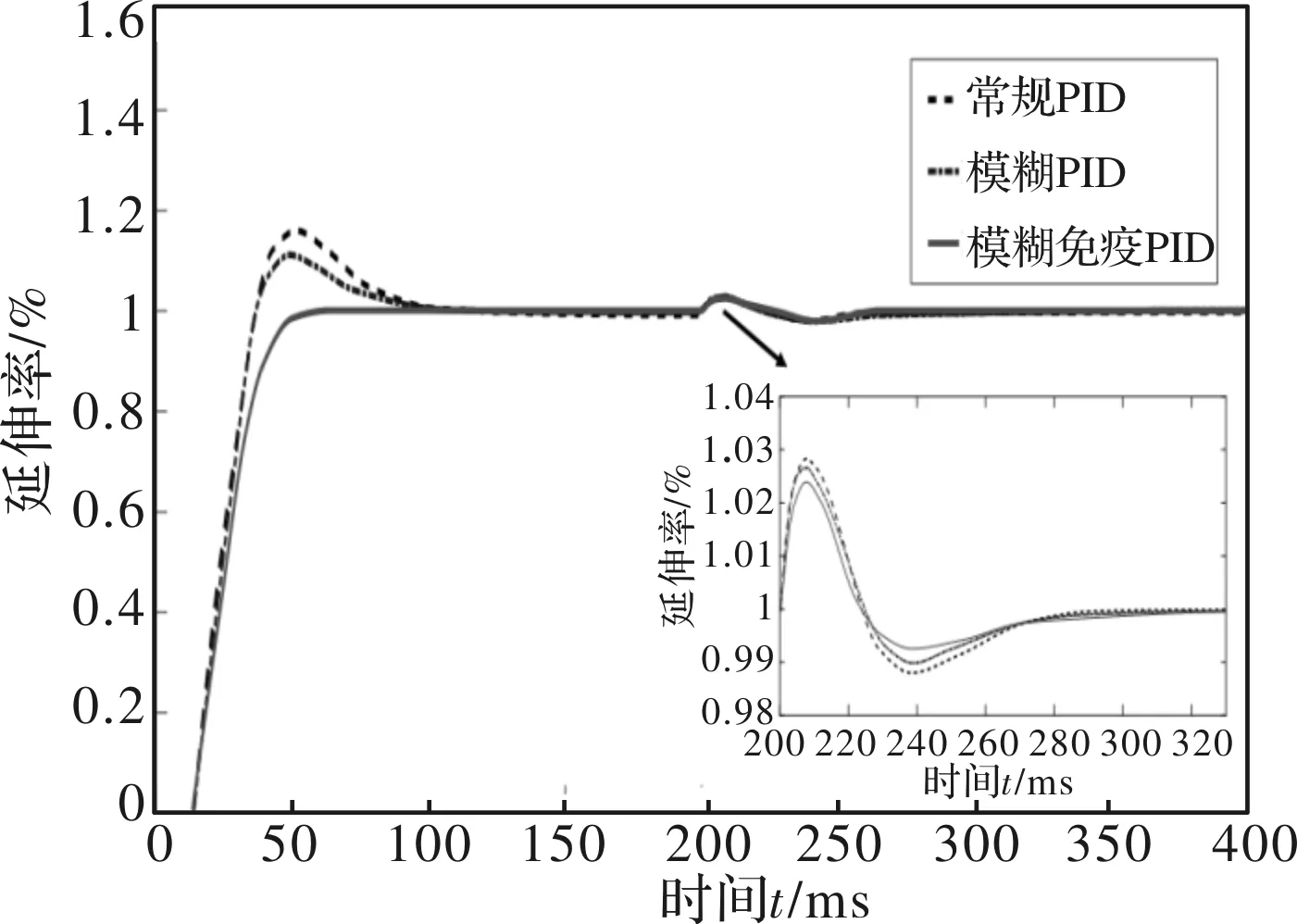
图11 不同控制策略的鲁棒性对比曲线

仿真结果表明，当模型失配时，基于模糊免疫PID的控制效果最好，系统具有较好的动态性能和较强的鲁棒性能，从而验证了模糊免疫算法优化PID参数的可行性和有效性。

5 结论

(1)平整延伸率控制系统是典型的双环控制系统，综合考虑系统各组成部件的动态特性，建立了平整机延伸率系统的机电液一体化机理模型；

(2)采用BP神经网络对平整延伸率控制系统模型进行参数辨识，辨识模型的输出与实际结果能够实现良好的拟合，辨识模型精度较高；

(3)利用模糊免疫PID对平整延伸率系统进行控制，其调控特性优于传统控制策略，且具有良好的抗干扰能力和鲁棒性。