宽厚板矫直方案对力能参数的影响

赵 岽

(太原重工股份有限公司矫直机研究所， 山西 太原030024)

0 前言

辊式板材矫直机由多个矫直辊对已变形板材连续施加相应的反弯，使板材经反弯弹复后残余曲率逐步减小，最终达到平直状态。矫直机的辊系参数受所需矫直板材的性能、规格、反弯要求以及零件机械强度的综合影响而保持相对固定值，因此辊系的矫直能力也处于一定的范围内；辊系参数是固定的，而矫直方案是多样的，不同方案设定的各矫直辊对轧件弯曲程度不同，所以不同方案所需的力能参数也是不同的，即使同一方案中各辊的力能参数也存在很大差异，通过多种矫直方案的应用，可以在相对固定的辊系参数条件下，达到提高设备矫直能力的目的。特别是宽厚板矫直机具有矫直板材强度高、力能参数大的特点，因此在计算力能参数时，一定要结合相应矫直方案的各辊曲率变化情况进行。

1 宽厚板矫直的主要方案

根据矫直原理，结合设备结构以及不同规格板材的矫直特点，常用的宽厚板矫直方案有4种：上矫直辊系整体调整大变形矫直方案、大变形小残差矫直方案、平行辊缝小变形矫直方案、小变形矫直方案。本文以某九辊宽厚板矫直机为例，研究各矫直方案的曲率变化。该矫直机辊径φ220 mm，辊距 260 mm。

1.1 大变形线性递减矫直方案

大变形线性递减矫直方案既可保证较高的矫直精度，又不至于消耗过多功率，适用于薄板和中等厚度板材的矫直。如矫直板材厚度8～25 mm、宽度1 200～3 500 mm、屈服强度σS为350～650 MPa时，矫直机各矫直辊下的相对曲率变化见表1[1]。

表1 上矫直辊系整体调整大变形矫直方案

1.2 大变形小残差矫直方案

大变形小残差矫直方案可有效提升高强度薄板的矫直精度，但设备结构与工艺参数设定比较复杂、功率消耗较大。当矫直板材厚度5～20 mm、宽度 1 200～2 800 mm、屈服强度σS为550～1 000 MPa时，矫直机各矫直辊下的相对曲率变化见表2[2]。

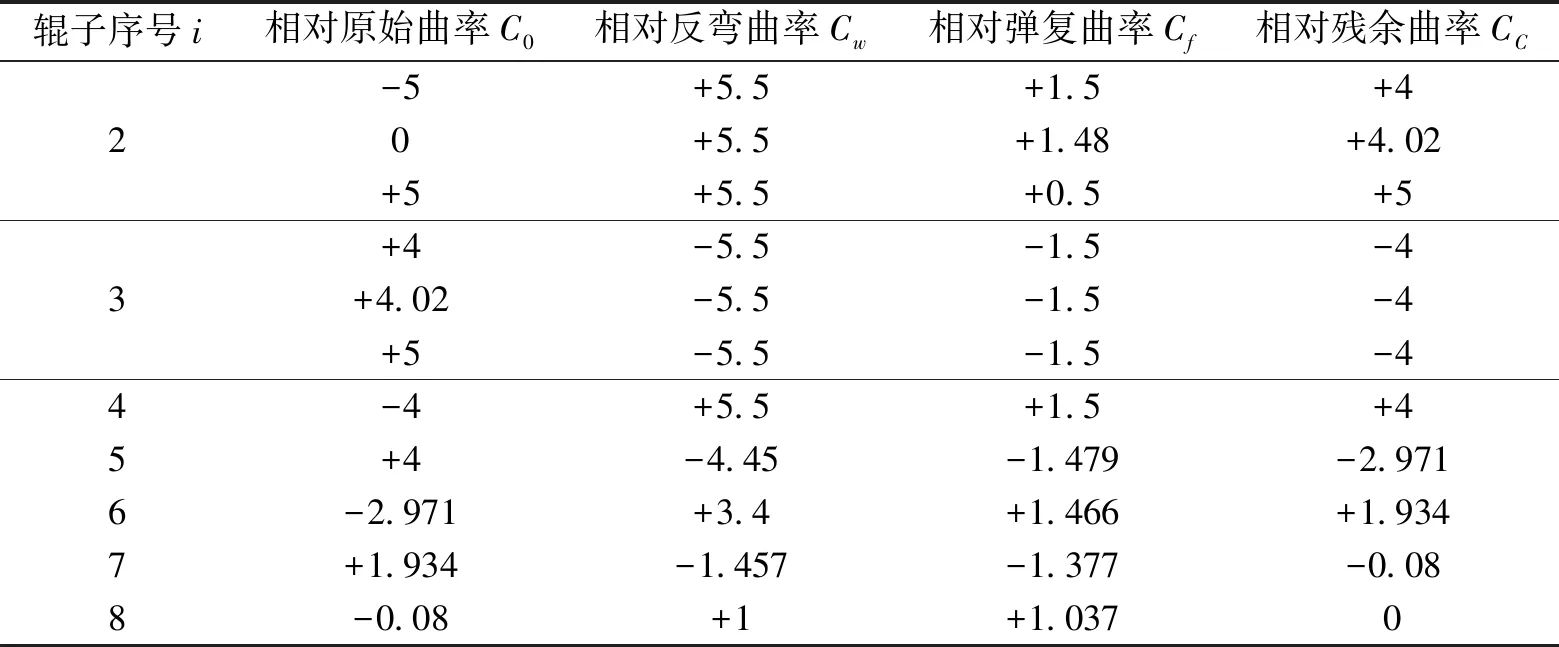
表2 大变形小残差矫直方案

1.3 平行辊小变形矫直方案

平行辊小变形矫直方案适用于中、厚板的矫直，工艺参数设定便捷，矫直力与矫直力矩相对较小，可有效避免负转矩的形成。当矫直板材厚度10～30 mm、宽度1 200～3 000 mm、屈服强度σS为450～600 MPa时，各矫直辊下的相对曲率变化见表3[3]。

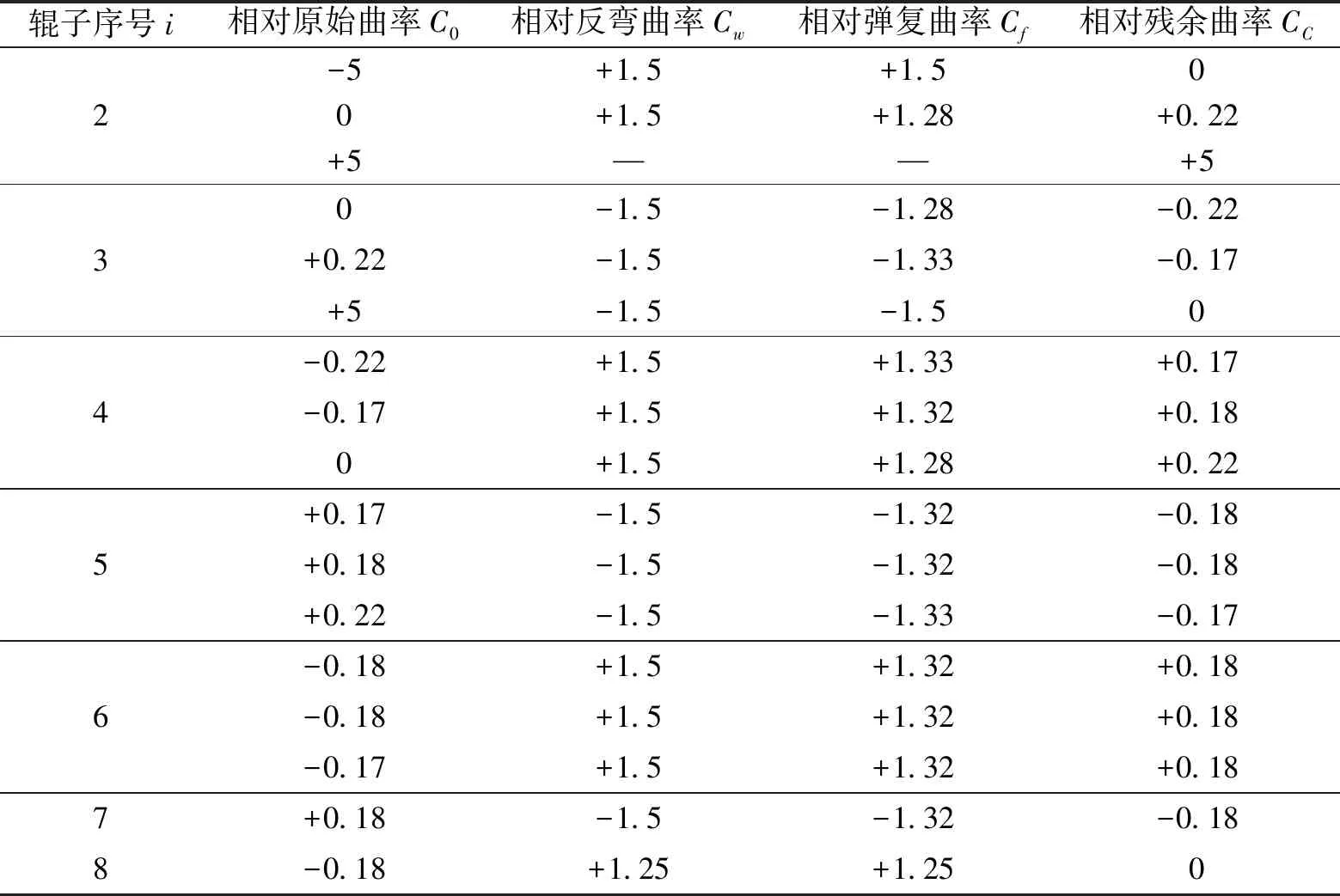
表3 平行辊缝小变形矫直方案

1.4 小变形矫直方案

小变形矫直方案具有压下量相对较小、功率消耗小的特点，适用于原始曲率较小的厚板矫直。设定各辊相对反弯曲率Cw(i)应使进入该辊轧件的最大相对原始曲率C0(i)能完全矫直，经反弯弹复后，最大相对残留曲率CC(i)是板材平直处反弯弹复后留下，并成为下一辊的原始曲率。采用该方案矫直厚度10～30 mm、宽度 2 800～4 300 mm、屈服强度σS为450～800 MPa的板材。各辊处设定的相对反弯曲率Cw(i)可通过求解矫直曲率方程得出。

Cw(i)3+(2C0(i)-1.5)Cw(i)2+(C0(i)2- 3C0)Cw(i)+0.5-1.5C0(i)2=0

(1)

再由弹复曲率方程式(2),得出Cf(i)。

(2)

计算残留曲率CC(i)=Cw(i)-Cf(i)作为下一辊的原始曲率，依次计算各矫直辊下的相对曲率变化见表4。

表4 小变形矫直方案

由表1～4可以看出，不同方案设定的各矫直辊对轧件弯曲程度不同，所以不同方案所需的力能参数也是不同的。

2 矫直方案对力能参数的影响

矫直力能参数主要包括矫直力和矫直力矩。通过四种矫直方案对矫直力、矫直力矩的影响进行分析，得出各矫直方案的力能参数计算方法。

2.1 矫直方案对矫直力的影响

在矫直过程中，各矫直辊对轧件施加连续反弯，使板材发生弹塑性变形，作用在各矫直辊上的力Pi，可由在辊距t间所受的弹塑性弯曲力矩Mi来决定，如图1所示。

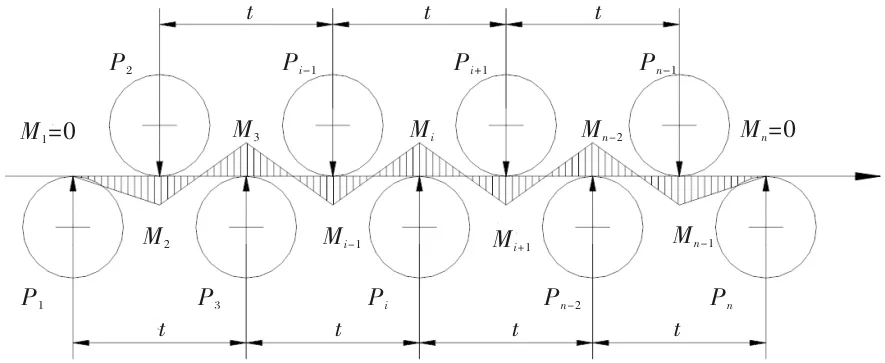
图1 作用在各矫直辊上的压力

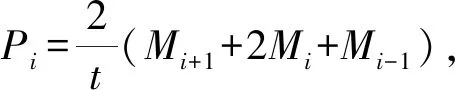
(3)

从总矫直力P可以看出，只要确定了各辊处轧件弯矩值Mi就可以得出矫直力。各辊处轧件弯矩值Mi决定于反弯曲率的大小；可根据板材规格、原始曲率C0(i)和相应矫直方案设定的反弯曲率Cw(i)按式(3)计算Mi。

(4)

(5)

(6)

图2 各辊相对矫直力变化曲线

由图2可以看出，不同矫直方案的矫直力差异还是比较大的，即使同一方案的各辊矫直力也存在很大差异。

2.2 矫直方案对矫直力矩的影响

矫直力矩T包括摩擦力矩Tm和弯曲变形力矩Tb。矫直方案对摩擦力矩和对变形力矩的影响。矫直力矩T的一般计算公式为

(1)矫直方案对摩擦力矩的影响。

(7)

式中，Tm(i)为各辊摩擦力矩；t为辊距,mm；d为轴颈,mm；f为轧件与辊面的滚动摩擦系数，取0.4 mm；μ为轴承摩擦系数，取0.005；

图3 各辊相对摩擦力矩变化曲线

(2)矫直方案对变形力矩的影响。计算各辊变形力矩Tb(i)不仅可以得出总变形力矩，而且也反映了相应矫直方案各辊变形力矩的变化规律。

(8)

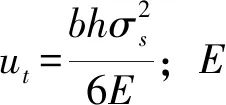
(9)

图4 各辊变形能量比变化曲线

由图3、图4可以看出，不同矫直方案的矫直力矩差异还是比较大的，即使同一方案各辊的矫直力矩也存在很大差异。

2.3 矫直方案对力能参数平均值的影响

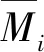
表5 相应矫直方案的相对力能平均值

3 不同矫直方案力能参数在各辊的分布比例

通过分析可以看出，不同矫直方案的矫直力矩差异还是比较大的，即使同一方案各辊的力能参数也存在很大差异。因此进一步总结4种矫直方案的各辊力能参数分布特点和计算方法，可为准确计算提供方便。

分别按图2、图3、图4中的各辊相对力能值计算各辊矫直力Pi占总矫直力P的百分比，各辊摩擦力矩Tm(i)占总摩擦力矩Tm的百分比，各辊轧件弯曲变形力矩Tb(i)所占总弯曲变形力矩Tb的百分比，结果见表6。

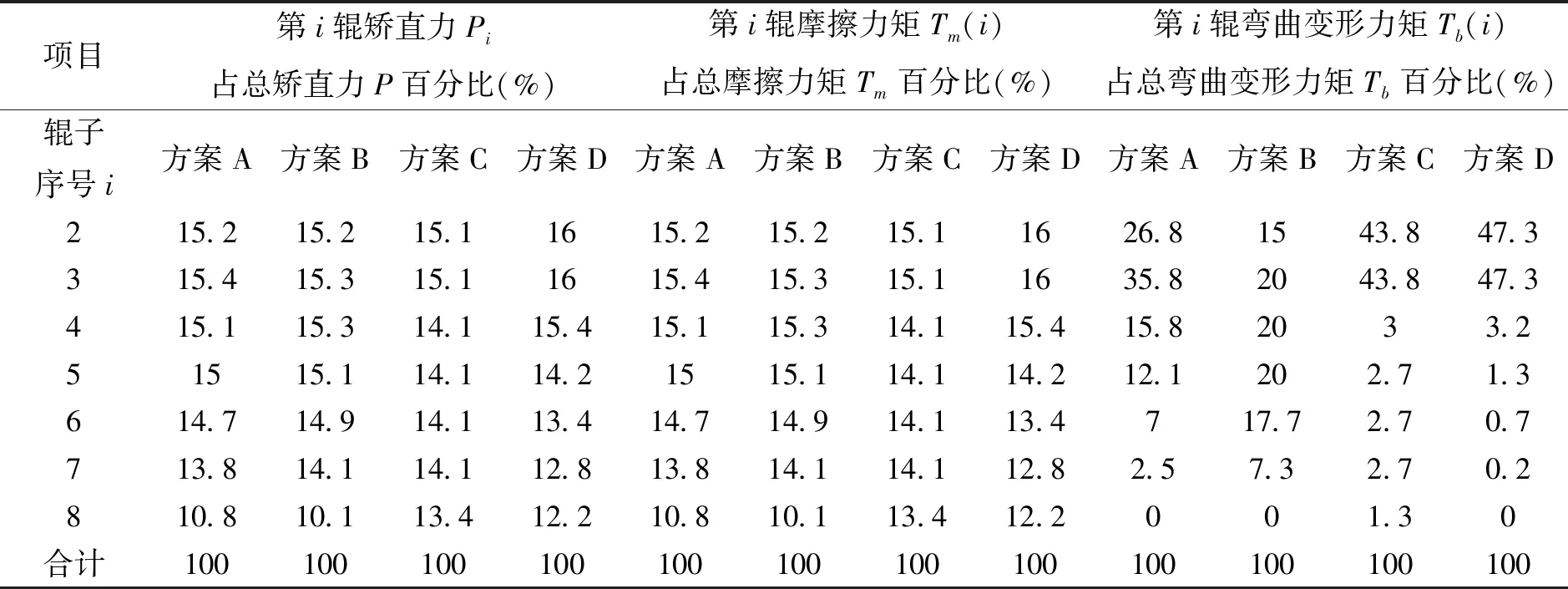
表6 相应矫直方案的各辊力能参数占比

注：A、B、C、D分别为上矫直辊系整体调整大变形矫直方案、大变形小残差矫直方案、平行辊缝小变形矫直方案、小变形矫直方案。

4 力能参数计算实例

通过分析，各主要矫直方案力能参数计算的理论问题已经解决，计算方法基本明确，以便深入理解和准确掌握。例如该九辊矫直机对确定规格的工件进行矫直，按上矫直辊系整体调整大变形矫直方案计算得到各项力能参数。矫直机技术参数见表7。

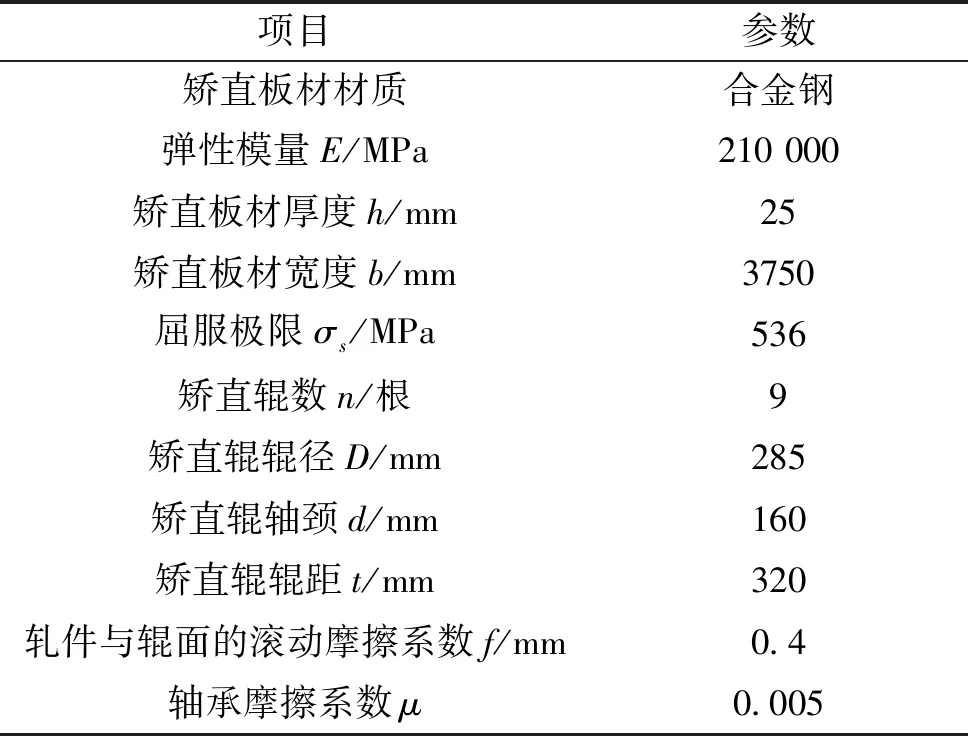
表7 九辊矫直机技术参数

4.1 计算矫直力P

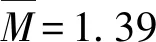
4.2 计算矫直力矩

T=Tm+Tb=171 452 832.5 N·mm

4.3 计算电机功率

式中，η为传动效率系数；0.7～0.9，取0.9；v为矫直速度；取v=1 m/s。同理，也可方便、准确的计算出其它三种矫直方案的力能参数。

4.4 计算各辊矫直力能参数

按表6中方案A各辊力能参数占比计算各辊力能参数，结果见表8。

表8 各辊矫直力能参数

5 结束语

宽厚板的不同矫直方案所需的力能参数值差异很大，在进行力能参数计算时，一定要结合相应矫直方案的反弯特点进行；采用相对值表达各项参数的方式可形成具有普遍意义的关系式，无论轧件断面尺寸、工件材质如何，在计算时只要结合具体的辊系参数和轧件规格，就可按相应矫直方案方便、准确的计算各项力能参数。这不仅为设备强度计算提供了依据，而且为矫直工艺的优化提供了参考，在生产实践中具有重要的指导意义。