固相浓度对旋流泵内循环流动结构的影响
权辉,康蕾,郭英,程静,于欣洋,权思哲
(兰州理工大学能源与动力工程学院,甘肃 兰州730050)
近年来,无堵塞杂质泵已成为国内外的研究热点[1].旋流泵作为一种结构特殊的杂质泵,被广泛应用于化工、矿山、污水处理、食品运输等各个领域[2-4].旋流泵因叶轮后缩到泵壳后腔的特殊结构使得其内部流动比较特殊[5].对固相参数及流场特性的研究是固液两相流水力输送主要研究方向之一[6-7].沙毅[8]通过输送清水和菜籽与水混合介质的试验,综合分析了内部流场与泵外特性变化之间的定性关系.该研究小组还将泵内阻力能耗分为机械和流动损失2部分,阐明了机械效率和流动效率经验计算公式,从而研究旋流泵输送固液两相流特性[9].钱姜海等[10]使用加载了群体平衡模型(PBM)的欧拉双流体模型,对固相介质对旋流泵外特性的影响规律进行分析,得到更符合物理真实的两相流动特征.权辉等[11]对旋流泵的基本工作原理和内部流动特性进行了分析,结合各国学者提出的几种经典的流动模型,提出循环流的存在是导致泵效率较低的主因.固液两相流的一个重要特征是由于体积分数不同导致流动的不平衡性,这种不平衡性在流体机械中最主要的2种表现形式是产生涡旋和分层现象,旋流泵流场内的循环流结构是以牺牲泵的传输效率为前提,增强了对大颗粒、条形物等介质的过流能力.研究固液两相流下固相体积分数变化对旋流泵循环流结构的影响,对分析泵内的能量转换规律、优化泵的结构设计有重要的意义.
1 数值方法
1.1 流场建模及网格划分
建立150WX-200-20型卧式旋流泵模型,其设计参数中,流量Qd=200 m3/h,扬程H=20 m,额定转速n=1 450 r/min,效率η=50%,轴功率P=26.34 kW.旋流泵的水力几何参数中,叶轮外径D2=250 mm,叶片宽度b=60 mm,叶轮叶片数Z=10,叶片厚度b2=8 mm;蜗室宽度L=70 mm,蜗壳无叶腔基圆D3=280 mm,蜗壳后缩腔环与叶轮的间隙e=30 mm,蜗壳无叶腔喉部面积Fthr=100 cm2.
旋流泵轴截面如图1a所示.利用Creo软件对该旋流泵计算域进行三维建模如图1b所示.
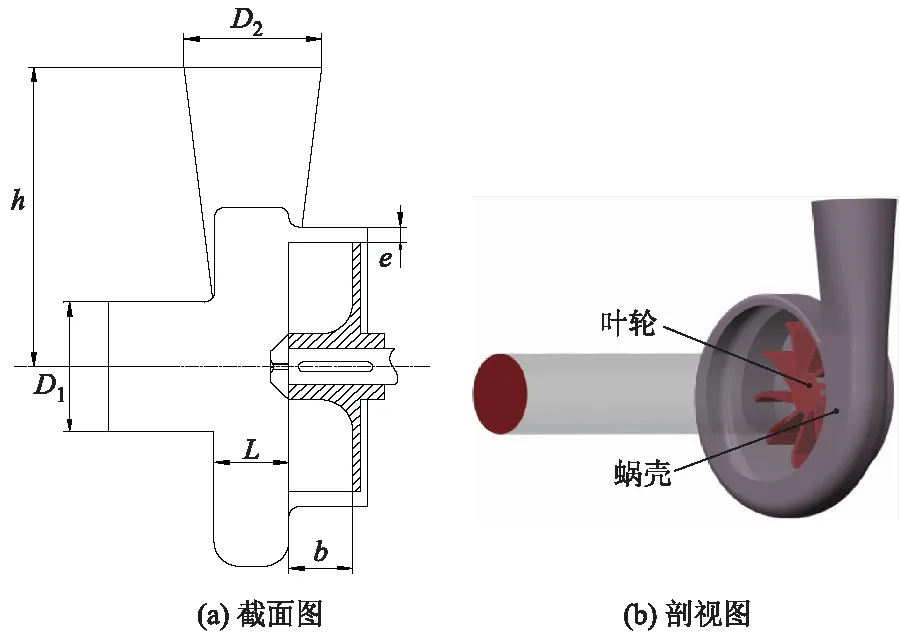
图1 旋流泵轴截面和剖视图
采用ICEM对三维模型进行结构化网格划分,将计算域分为静止域与转动域,即叶轮域、蜗壳域两部分,设置2个耦合面处理动静干涉,以网格加密处理的方式调整边界层以及隔舌处的网格.在进行网格划分时,为更准确捕捉壁面黏性对流体的影响,在划分网格过程中添加了边界层网格,网格层数为10层,壁面附近第1层网格厚度为0.01 mm,壁面y+<15,满足要求.
对模型泵网格进行网格无关性检查,以尽可能保留流场计算信息为前提,最大程度减小网格尺度对计算精度的影响。对静止域采用了2种网格划分方式,对转动域用了4种,共组成了网格数分别约为211万,256万,305万,325万和381万这5套不同尺度的计算网格,验证网格无关性时,对5套网格采用RNGk-ε两方程湍流模型在设计工况下对单相清水介质进行定常计算,结果发现在网格数大于300万时,扬程变化小于1.5%,综合考虑后选择第3套网格进行数值计算.最终得到了如图2所示的整体计算域及网格划分的结果,A-A,B-B分别为经过第2,6断面和第4,8断面的轴截面.
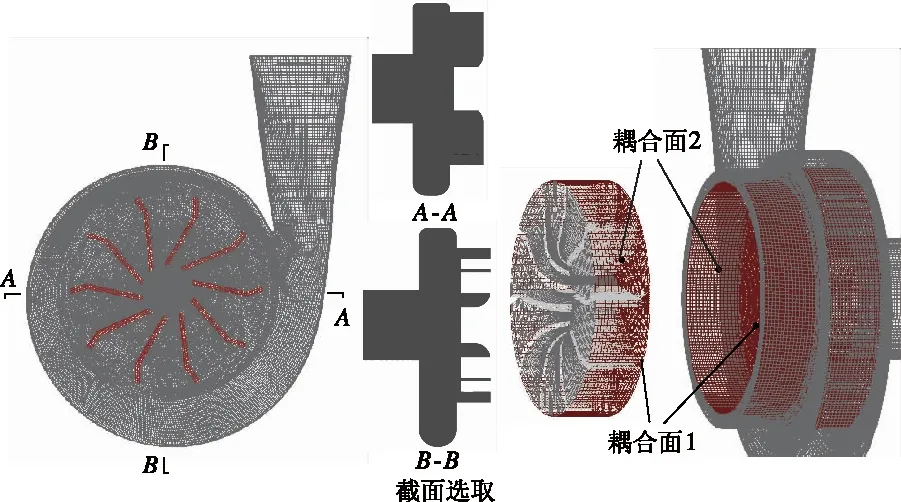
图2 计算域网格及研究截面选取
1.2 旋流泵变浓度内部流场的数值计算
对于旋流泵内不可压缩流动,采用ANSYS Fluent进行数值计算.两相流选用的模拟介质为含沙水,第1相为常温清水,第2相为密度ρ=2 250 kg/m3、粒径d=4 mm的球形颗粒,考虑重力,不考虑相变.由于旋流泵内流结构的特殊性,固相分布较为集中,因此对泵内固液两相流选用Eulerian双流体模型[12].采用SIMPLE压力修正算法求解压力耦合方程组,以考虑相间滑移,利用动静参考系控制流体及叶轮的运动方向,叶轮域采用Frame Motion.采用在旋涡、强流线弯曲等方面有较好表现的RNGk-ε湍流模型.计算域的进口采用速度进口条件,假定进口处颗粒体积分数均匀分布且速度相等;出口采用自由出流;全流道内与液体相接触的面,对于流体相采用无滑移壁面条件,固相颗粒采用自由滑移壁面条件.
对泵内清水亦选用RNGk-ε湍流模型.边界条件设置与两相流相同.
2 试验测试与可靠性分析
2.1 试验测试台系统
为验证数值计算结果可靠性和准确度,建立旋流泵开式试验测试系统,以介质为单相清水时对同一模型进行试验测试和数值模拟,如图3所示.
2.2 试验测试性能结果比较
对试验测试与数值计算的外特性结果进行对比,如图4所示.由图4分析得,随流量增大,试验泵与数值模拟模型的测试所得的水力性能存在误差,经计算,扬程和效率的平均误差分别为2.27%和5.26%,误差在可接受范围之内,这间接说明文中采用的数值方法对于研究该旋流泵是可靠的.
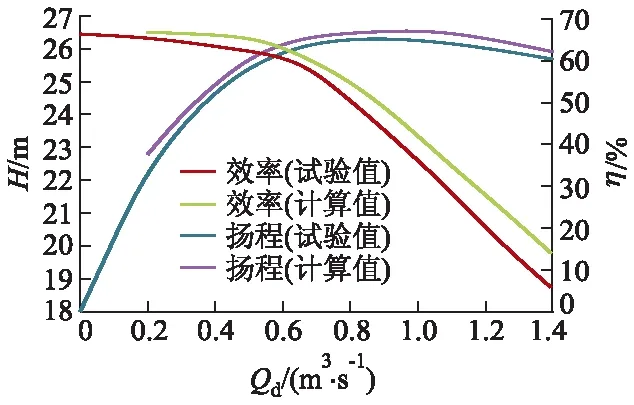
图4 水力性能误差验证
3 固液两相流时旋流泵内流结构特性
3.1 输送清水与固液两相流的区别
图5为额定工况下模拟固相体积分数Cv为0和10%得到的旋流泵内截面A-A与B-B的介质流动流线图,图中Ⅰ,Ⅱ等为涡序号,v为流体速度,同一股循环流由两截面内同一序号的涡结构表征.
由图5可以观察到,2种介质工况下,液相质量力较小,因此流向易发生改变,在进口流速较大时,在叶片间流道加速后由轮缘处流出的流速较大的流体,流入无叶腔时其流体黏性与斜压力作用共同形成了尺度不等的强制涡,且无叶腔作为控制体,其内部流动边界固定,故在环形流道内形成了相互制约的多组循环流.随着无叶腔断面面积增大,Ⅰ与Ⅰ′代表的主循环流动逐渐减弱,Ⅱ与Ⅱ′代表的次循环流逐渐增强.单相流下,在泵流场内部,介质流线较固液两相流下更为紊乱,除主循环流外,还存在其他几组流动较弱的循环流,能量耗散较大.固液两相流下,由轮缘流出的固相流速较大且矢量方向不易改变,因此液相的流动方向受固相拖曳力反作用而形成了尺度较大且形状较规律的主循环涡,又因固相颗粒主要聚集于无叶腔底部远离轴线的区域,一定程度挤压了循环流Ⅱ的流动区域,又因固相介质流向不易变化,因此较少参与循环流动中.总而言之,在额定工况下,因固相加入,泵无叶腔内的液相流动规律改变较明显,各个断面上涡结构数量减少,在主流涡尺度增大的同时,次流涡尺度减小.
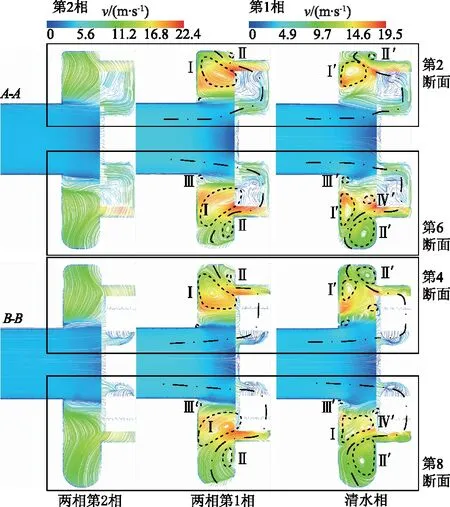
图5 清水与两相流时旋流泵内部流动流线图
3.2 固液两相流时旋流泵内流结构
3.2.1 旋流泵内部流动结构
旋流泵内固液两相流下,固相因质量力较大的缘故,较少参与液相的循环流运动,因此只需研究不同介质以及流量工况下无叶腔各断面上液相形成的涡结构的尺度与位置变化规律从而加深对旋流泵内流场中循环流的理解,各个断面均存在约2至3个尺度较大的涡结构,循环流由各断面相近位置的涡连接形成,随工况改变,涡结构在无叶腔内沿轴向产生位移,其连接形成的涡带或涡环可相互转变,如图 6所示,将液相流动情况表达于无叶腔内的4个1/4截面上,图中所示3种不同色的曲线分别表征涡结构 Vor1,Vor2,Vor3在无叶腔内连接而成的涡环或涡带,叶轮工作时,介质的运动轨迹为“T→L→B→R”,其中T,L,B,R分别代表 4个无叶腔断面,T,B与L,R上的涡结构几何特征分别由截面A-A,B-B的后处理分析得出.
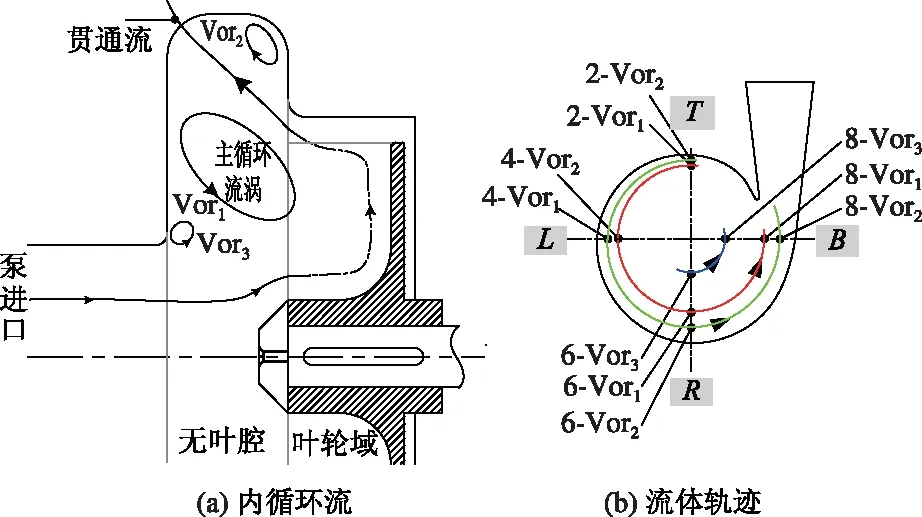
图6 旋流泵内流结构示意图
表征次循环流Ⅲ的Vor3尺度远远小于主循环流,且主循环流涡介质的流速远大于次流涡,故重点考虑主流涡与泵的外特性能之间的联系.所选截面上的流线即液相速度矢量在各无叶腔断面上的投影形成的涡结构近似椭圆,且其形状及位置的变化规律有迹可循,因此分析截面上 Vor1的几何特征的变化规律,以探究各工况下固相浓度变化时泵外特性与流场内循环流之间的关联.
3.2.2 表征参数确定
Swirling Discriminant是CFD-post提供的利用求解速度梯度张量的判别式,以其计算结果的正负判别涡核的存在性,当判别式为正时,即认为涡旋在该区域存在,如图7a所示的三维涡旋分布图,可观察到泵无叶腔内循环流Ⅰ,Ⅱ所在的位置存在2条绕轴的涡带或涡环.
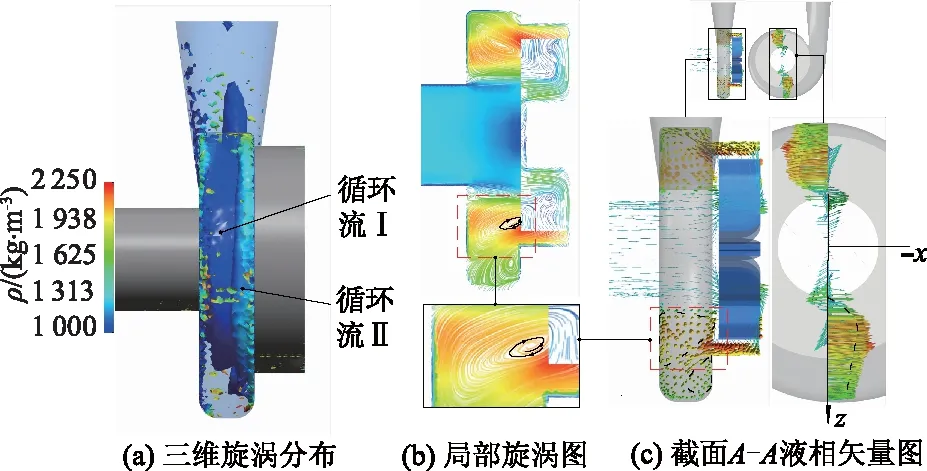
图7 旋涡判别示意图
涡旋内存在类似刚体旋转的一个涡量密集区域,即涡核,周围流体绕其做近似圆周运动而形成涡旋.如图7c所示,虚线大致标记的范围,液相的矢量与圆周方向相切,从图7b中该截面的流线图中可观察到,周围流体在该截面上在某一位置做近似圆周的绕流,从而逐渐无限接近在该截面上矢量分量减弱的区域,无叶腔内各断面上均存在该现象,假定将所有的极限点连接成线,其上所有的流体质点同该情况下旋转角速度矢量与此线相切,即涡线.以此对泵涡旋的涡核位置可进行一个大致的判别[13].
对于旋流泵,无叶腔内的循环流在轴截面上以涡结构呈现,且流线大多为圆,或者是近似为圆形的椭圆,椭圆的曲率中心在椭圆内形成简单的星形线轨迹.CFD-post中对模拟结果进行分析时,在介质流线足够密集的情况下,将椭圆状流线的曲率中心固定在较小的范围内,为统一表达,将涡旋内靠近涡核位置的流线近似为椭圆弧度的一部分,椭圆曲率中心在圆心附近的范围,故近似认为椭圆状流线的圆心位置为涡核位置,因此可将点C看作该涡旋流场中与涡线相垂直的无叶腔截面上涡核所在的位置.m,n分别为截面A-A,B-B上涡核与轴线的距离以及涡核与无叶腔中心面的距离.在旋流泵中,各截面上的涡核位置的变化范围远远大于所得到的涡核位置与实际位置的误差值,因此认为此种判别方式在文中是可行的.
鉴于循环流涡结构呈类椭圆形,同时靠近涡核位置的流线接近于如图8b所示的椭圆,故可通过偏心率e(0 图8 涡核位置与形状系数 (1) 式中:a,b分别为椭圆的长轴和短轴. 对比分析固相浓度对旋流泵性能及内部循环流动的影响,选取固相体积分数Cv=10%,15%,20%,25%,30%,35%.选取0.6Qd~1.4Qd中等分的5个工况的计算结果进行分析,固相体积分数增大时其扬程减小,进口流量增大时扬程亦减小.效率在不同体积分数下均在 1.2Qd时达到最高,且同工况下体积分数增大,效率降低.图9为不同工况下主循环流截面涡结构的涡核位置,其中m=125 mm为1/2D2,n=35 mm为无叶腔右侧与叶轮域左侧的交界面,n=-35 mm处为无叶腔左侧靠近进口的壁面,n=0 mm处为无叶腔中面. 由图9a可知,在0.6Qd~1.2Qd时,2-Vor1的涡核位置始终在无叶腔内,当流量增大至1.4Qd时,涡核进入叶轮域,涡结构在叶轮旋转的作用下被破坏,产生较大能量耗散.对Q-m,2-Vor1的涡核位置随流量增大由无叶腔左侧逐渐向右侧移动到叶轮域,对Q-n,涡核位置随流量增大逐渐靠近轴线.分析图9b可知,4-Vor1的涡核均在无叶腔内.对Q-m,4-Vor1的涡核位置随流量增大由无叶腔左侧逐渐向右侧移动且不进入叶轮域,对Q-n,涡核位置随流量增大逐渐靠近轴线;对2-Vor1,4-Vor1的涡核位置,对Q-m,在m=125 mm处,前后2个工况下m值随Cv变化的趋势改变.前一个工况,Cv越大,m值越小;后一个工况,Cv越大,m值越大.对Q-n,涡核位置在无叶腔右侧,随流量增加速度较左侧运动明显增大. 由图9c可观察到,6-Vor1的涡核均在无叶腔中心面右侧.不同固相体积分数下,涡核位置变化随流量的变化影响均较小.由图9d可观察到,当10%≤Cv≤15%,在1.2Qd~1.4Qd工况下,以及当20%≤Cv≤35%,在1.4Qd工况下,不存在明显的8-Vor1,在上述体积分数及流量下,旋涡在第6到第8断面中的某一1/4轴截面上终止于n=-35 mm处的无叶腔左侧壁面边界.对8-Vor1存在的工况下,在0.6Qd~1.0Qd时,对Q-m,涡核由无叶腔中心面的右侧向中心面运动,对Q-m,涡核与轴线距离随流量增大而减小.在1.0Qd~1.2Qd工况下,对Q-m,涡核由无叶腔中心面向无叶腔左侧快速运动,对Q-n,涡核位置快速远离中心轴线,体积分数越小,在0.6Qd工况,与无叶腔中心面距离越远,与中心轴线距离越远;在0.8Qd工况,与无叶腔中心面距离越近,与中心轴线距离几乎相同,在1.0Qd~1.2Qd时,与无叶腔中心面距离越近,与轴线距离也越近. 对Cv=10%,15%,25%,35%在不同工况下模拟结果做近似处理,计算得到表征涡形状的形状系数e,获得如图10所示的涡结构变化规律图. 图10 涡结构形状变化 由图10可观察到,2-Vor1的e值在[0.6Qd,1.0Qd]区间内为正增长,而后随流量或浓度变化,其值在较小的范围波动,对比分析图9中的涡核位置变化,随进口流量增大,2-Vor1位置在无叶腔内轴向运动趋势为逐渐靠近叶轮域,其形状的变化趋势为由圆至扁,在靠近叶轮域与无叶腔交界面时,e值小幅度减小,而后随流量增大,涡旋向叶轮域发展.各浓度下,4-Vor1的形状在[0.6Qd,1.0Qd]区间内变化不明显,但随流量增大在高效点1.2Qd会出现e的极值.各浓度下,6-Vor1的形状在[0.6Qd,1.4Qd]区间内e波动范围较小,但值均较大,在1.4Qd工况下,固相浓度越大,e值越小,涡形状越扁.各浓度下,8-Vor1的e值均随流量增大呈正趋势增长,且浓度越大,其增大的幅度越小. 由图10还可以观察到,表征的主循环流的涡结构,其形状与位置随工况变化的趋势因无叶腔空间的限制会相互影响,在各浓度下,1.2Qd工况时,各截面上的涡结构的形状系数e值均较大.该点为固液两相流时该旋流泵模型在不同体积分数时相同的高效点,在该工况下,旋流泵截面A-A,B-B上4个断面的主循环涡的形状均比较扁平,同一介质工况下,涡结构的形状系数e的标准偏差达到最小值.在1.2Qd工况下,固相浓度越大,各个截面上涡结构的形状系数越小,即固相浓度越大,各截面上涡结构形状越圆,与此同时,泵对介质的输送效率越低. 1) 固液两相流时旋流泵内循环流Ⅰ,Ⅱ分别随断面面积增大轴面投影图面积逐渐变大和变小.固相颗粒对旋流泵内的流动结构的影响在于固相的介入普遍会增大主流涡的尺度且约束次流涡尺度的扩展. 2) 提出一种旋流泵内部流动模型,其内部存在1组主循环流和2组次循环流,Vor1表征主循环流在泵内1/4轴截面的涡结构.固相体积分数越大,主循环流在无叶腔内随着流量增大的运动范围越小.涡核均在无叶腔内的工况下,效率随流量增大而增大,而当涡核随流量增大进入叶轮域被破坏后,泵效率降低.在高效点1.2Qd,固相体积分数越大,涡核与轴线距离m越小. 3) 流量与固相参数对旋流泵内的循环流结构有较为明显的影响,这与泵的水力性能有必然的联系.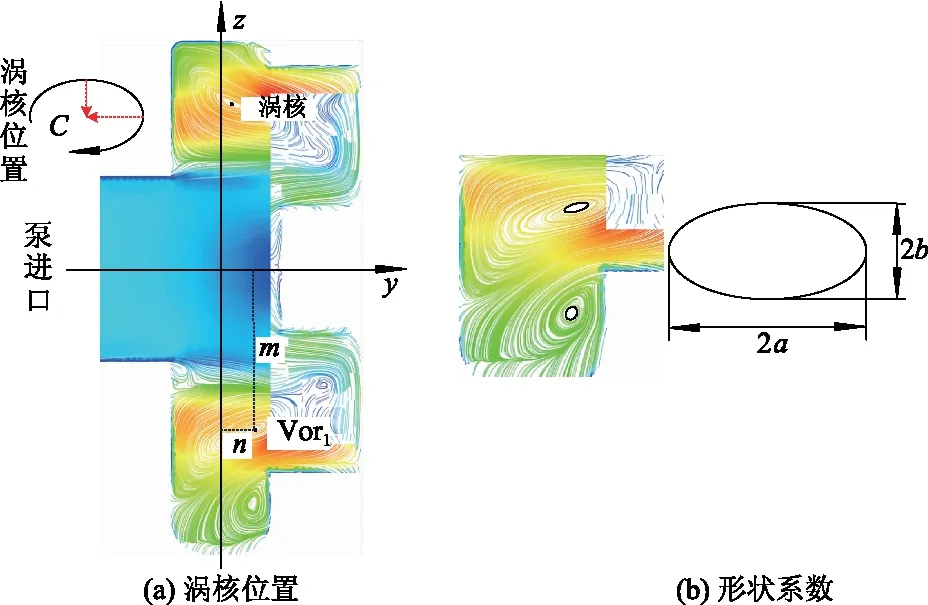
4 固相浓度对旋流泵内循环流的影响
4.1 涡核位置的变化
4.2 涡形状的变化

5 结 论

