波浪补偿控制算法综述

唐刚，胡超，姚小强，李建霞，韩重阳，邵辰彤，胡雄

(上海海事大学物流工程学院，上海 201306)

船舶上工程机械的运动是船舶在波浪的作用下产生运动和工程机械本身驱动作用下产生运动的耦合，将船舶在波浪的作用下产生的运动从船舶上工程机械的运动中解耦出来，并进行相应补偿的技术称为波浪补偿技术.近年来，武汉第二船舶设计研究所的王哲骏等[1]在波浪补偿系统工作原理和波浪补偿装置的发展现状2个方面进行了文献综述，对波浪补偿系统技术的发展趋势进行分析.WOODACRE等[2]从升沉补偿的基本原理、潜水器出水和入水时的波浪同步技术和驱动方式3个方面进行了文献综述，分析控制系统中存在的问题，并指出未来控制系统的发展方向为带有前馈预测的控制系统.白玉等[3]分析了海上并靠补给的被动式波浪补偿技术和主动式波浪补偿技术的现状，并指出六自由度波浪补偿技术是未来的发展方向.目前应用在波浪补偿领域的控制算法主要分为两类：一类是通过估计运动轨迹的前馈控制算法，估计运动轨迹的方法主要有卡尔曼滤波、神经网络和时间序列分析法；另一类是通过减少误差的反馈控制算法，主要有PID控制算法和模型预测控制算法.

文中采用的是前馈控制和反馈控制的分类方法，以便于更好地阐述波浪补偿技术的发展.

1 前馈控制算法

1.1 卡尔曼滤波

1.1.1 原始卡尔曼滤波

早期的主动式波浪补偿预测方法主要采用卡尔曼滤波法，EL-HAWARY[4]通过对海上作业的船舶运动进行实时预报来消除补偿中的时延.SIDAR等[5]利用卡尔曼最优滤波理论设计了航空母舰离散信号的预测器.

使用卡尔曼滤波对船舶运动进行预测，将一定海况、航速以及航向的船舶运动模型看作一个线性定常系统，它的运动实际上是一个平稳随机过程.通过线性定常系统传递函数最小实现方法，可以得到船舶运动状态空间表达式，即

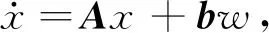
(1)

z=cTx+v,

(2)

将式(1)，(2)离散化得到船舶运动的离散模型为

xk=φk,k-1xk-1+Γk,k-1wk-1，

(3)

zk=Hkxk+vk，

(4)

TRIANTAFYLLOU等[6]使用卡尔曼滤波技术研究DD-963驱逐舰的升沉、俯仰、滚转、摇摆和偏航运动的预测.

1.1.2 扩展卡尔曼滤波

为避免计算中舍入误差和截断误差的累积引起卡尔曼滤波的计算发散,BIERMAN等[7]提出了平方根滤波算法、UD分解滤波、奇异值分解滤波等一系列算法,以确保在卡尔曼滤波增益回路中的滤波方差矩阵始终正定.

使用扩展卡尔曼滤波算法和增广的状态方程构成一种船舶运动模型参数辨识算法，用该算法来计算船舶运动模型中的未知参数.首先，建立船舶水平面运动模型，数学表达式为

x(t)=f[x(t),s(t),t]+w(t),

(5)

y(t)=Hx(t)+e(t),

(6)

s(t)=[δ(t),n(t)]T,

(7)

f=[f1,f2,f3]T,

(8)

H=I3×3,

(9)

式中：x(t)为状态方程的预测值;y(t)为观测方程的观测值；w(t),e(t)为零均值白噪声序列，方差分别为Q和R；δ为船舵角；n为螺旋桨转速.

PERERA等[8]提出了一种可用于船舶状态预测的扩展卡尔曼滤波器(EKF),并进一步将其用于船舶轨迹的预测.

1.1.3 自适应卡尔曼滤波

目前,在姿态运动预测领域中,扩展卡尔曼滤波是应用最广、最成熟的非线性滤波方法[9].原始卡尔曼滤波和扩展卡尔曼滤波应用不精确或错误的模型和噪声统计设计卡尔曼滤波器，会导致滤波器失去最优性,估计精度大大降低,严重时甚至使滤波发散.为了解决这个矛盾,近些年来产生了自适应卡尔曼滤波算法[10].自适应卡尔曼滤波算法流程图如图1所示，图中X为自适应卡尔曼滤波状态估计值，P为预测误差方差矩阵，q为系统干扰均值，Q为系统干扰方差矩阵，r为量测噪声均值，R为量测噪声方差矩阵，k为第t(k)时刻.

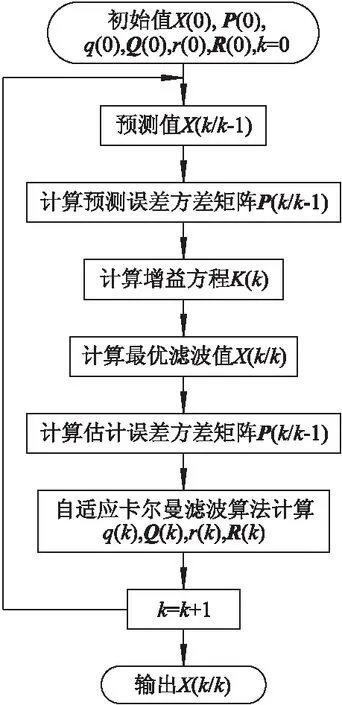
图1 自适应卡尔曼滤波算法流程图

在实际工程应用中，外界条件的改变可能使噪声统计特性发生变化，导致滤波发散[11].因此，需要在递推滤波的同时，实时估计系统噪声和量测噪声，进而研究出一种指数加权法的时变噪声统计估值器[12].FUNG等[13]使用自适应卡尔曼滤波器对船舶进行动态定位.

1.2 神经网络

1.2.1 DRNN(对角递归神经网络)

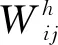
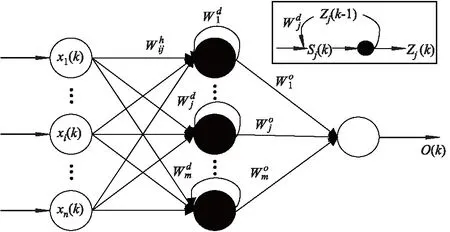
图2 对角递归神经网络的结构示意图

(10)

式中:φ(·)为非线性函数，常用Sigmoid函数.

DRNN还有与其配套的训练算法，其数学模型为

(11)

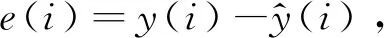
(12)

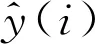
表1为DRNN算法研究对比分析表.如表所示，王科俊等[16]将当前测量的横摇时间序列值和前一时刻的横摇预报值作为网络仅有的输入值，预报下一时刻的横摇预报值.通过最速下降法训练对角递归神经网络，多次训练确定网络的权重值.SHEN等[17]将前一段时刻的俯仰通过改进的牛顿-高斯迭代法训练对角递归神经网络，通过多次训练确定网络的权重值.窦金生等[18]引入了时差(TD)学习算法结合最速下降法训练对角递归神经网络，时差学习算法通过对不同时刻各个神经元的输出值的变化，来调节该神经元权重调节的概率.

表1 DRNN算法研究对比分析表

1.2.2 BP神经网络模型公式

1986年，RUMELHART和MCCELLANDZ提出了BP网络模型,结构如图3所示.设BP网络的输入层有n个节点，隐含层有q个节点，输出层有m个节点，各个神经元的权重为w，偏置项为b，输入层与隐层之间的权值为vki，隐含层与输出层之间的权值为Wik，传递函数为f.

图3 经典3层BP神经网络结构图

隐含层节点的输出为

(13)

输出层节点的输出为

(14)

隐含层节点个数是不确定的，通常根据经验公式来确定，即

(15)

式中：p为1～10之间的常数.

BP神经网络的主要目的就是反复修正权值和阈值，使得误差值达到最小，即

(16)

BP神经网络通常使用下面2种非线性激活函数：

(17)

(18)

曾智刚[19]设置Elman网络的输入层、隐层、承接层和输出层神经元的格式为5-15-15-4.秦明杰[20]将波倾角α(t)作为输入，横摇角φ(t)作为输出，网络只采用1个隐含层，迭代29次后误差即可满足要求，如表2所示.

表2 BP神经网络算法在波浪补偿的应用层面与异同对照表

1.2.3 RNN的网络结构以及原理

1个最简单的RNN，如图4左侧所示，只有1个神经元接受输入，只产生1个输出，并将输出传递给自己.神经元可以随时间序列展开，如图4右侧所示.每个神经元都有2套权重，用于本层输入xt和用于上层输出yt-1的分别记为wx和wy.

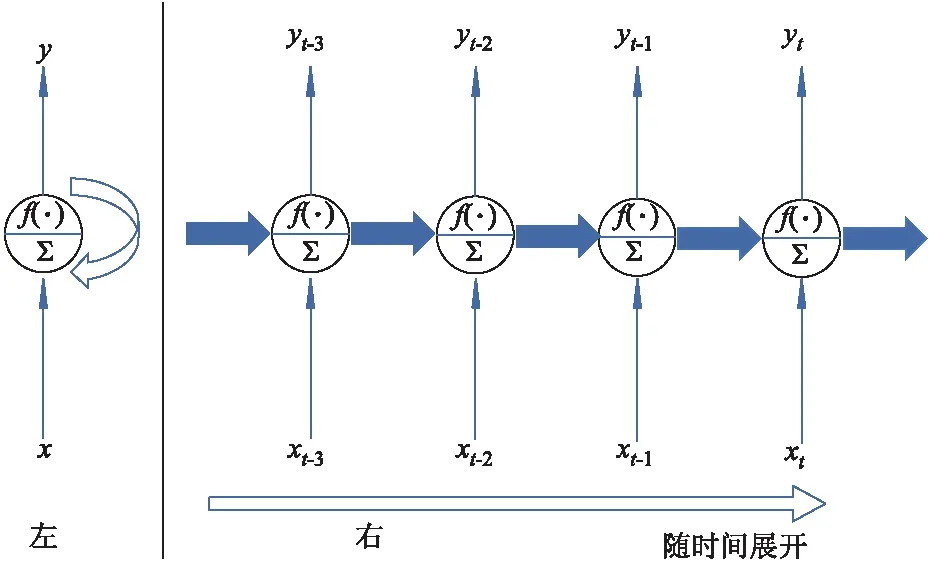
图4 RNN的网络结构图

1个循环神经元关于1个实例的输出：

(19)

φ(…)为激活函数(一般为tanh，也有用ReLU)，b为偏置项.

(20)

如表3所示，王国栋等[22]建立了基于LSTM的模型，对其进行了船舶姿态预测仿真.张东晓等[23]提出了一种基于循环神经网络的测试曲线生成方法，并进行了试验验证和应用效果分析.

表3 LSTM神经网络算法异同对照表

1.3 时间序列分析法

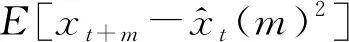
ARMA(p，q)模型的数学表达式[24]为

x(t)=φ1x(t+1)+φ2x(t-2)+…+φpx(t-p)+ε(t)-θ1ε(t-1)-θ2ε(t-2)-…-θqε(t-q),

(21)

式中：p，q分别为模型的自回归阶数和平移平均阶数；φ和θ分别为自回归系数和移动平均系数；ε(t)为独立的误差项；x(t)为当前的预测值.

DUAN等[25]提出混合AR-EMD-SVM模型来预测船舶的运动姿态.

2 反馈控制算法

2.1 PID控制算法

自从1910年发明PID控制(主要是Elmer Sperry的船舶自动驾驶仪)和1942年的Ziegler-Nichols(ZN)直接调整方法以来，超过90%的工业控制器仍然基于PID算法实现.PID控制算法的基本模型为

(22)

式中：G(s)为PID传递函数；kp为比例系数；ki为积分系数；kd为微分因数；Ti为积分时间常数；Td为微分时间常数.

PID控制算法在波浪补偿的运动控制中的应用，如表4所示，国内外的学者做了相关的研究.对于积分项的调节，BOHN等[26]通过控制积分量的过量积分作用来调节积分项在3个分量中的比重，以控制相位的滞后.为提高PID控制的自适应性和鲁棒性，有学者将智能算法引入PID控制中，方千山[27]引入了模糊盒树法自适应PID算法，通过对常规PID控制系统性能品质的分析，提出一种PID控制策略，利用模糊盒树的分枝定界算法，以最少的模糊规则推理实现PID参数的自适应调整.该方法具有结构简单、鲁棒性强、动态品质优良的特点.

表4 PID算法研究对比分析表

2.2 模型预测控制(MPC)

DO等[28]通过对液压系统进行建模，考虑到模型的准确性，采用Lyapunov非线性控制策略.KÜCHLER等[29]通过仿真和试验验证了MPC的效果，并提出了新的评价标准，定义一个衡量控制算法性能的物理量，即

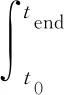
(23)

式中：Δzp为位移的变量；P为性能因子.

下面将详细介绍MPC：

1) 例如非线性起重机在状态空间中的模型[28]为

(24)

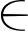
2) 控制的原则就是找到1个u(τ)(其中τ∈[t,t+Nc]，其中Nc为设置的控制范围)，使得目标函数取最小值.建立的目标函数为

(25)

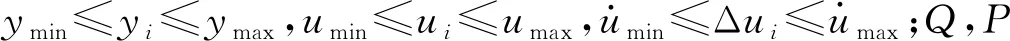
如表5所示，有很多学者将MPC及MPTP应用于波浪补偿研究[29-30].WOODACRE等[30]用无载开环液压AHC试验的MPC跟踪加载运动，发现由于液压过大导致液体泄漏，加载的系统运动滞后于无载的系统运动.

表5 应用于波浪补偿领域的MPC及MPTP的性能对比

3 结 论

1) 卡尔曼滤波算法在波浪补偿中的预测精度和收敛速度与过程激励噪声协方差Q，状态转移矩阵A以及测量噪声协方差R紧密相关，未来的研究可以通过不同的算法寻找最优的矩阵Q、矩阵A以及矩阵R，以提高波浪补偿的精度和收敛速度.

2) 神经网络算法主要是利用网络结构、网络权重和阈值的自适应调节实现对波浪上船舶的运动轨迹的估计.为提高算法的在线识别能力，可以将神经网络的结构进行调整，也可以改变神经网络的非线性函数，以实现对运动轨迹的高速、高精度的估计.

3) 时间序列分析法的波浪补偿模型是通过采集历史数据建立的，为防止波浪补偿模型过拟合导致计算量过大，精度下降，可以通过改进波浪补偿模型的适用性检验准则来确定波浪补偿模型的最优阶数以及模型的各项参数，保证波浪补偿模型预报精度的同时提高预报速度.

4) PID运动控制方法在波浪补偿中应用最为广泛，通过对误差的比例、积分和微分操作对机械系统输入控制信号进行反馈调节，控制波浪补偿系统的静态误差和动态误差在较小的范围内，未来可以通过改善PID控制算法的积分环节和微分环节，以及PID 3个参数的自适应调节环节，提高PID控制算法在波浪补偿运动控制领域的自适应性.

5) 模型预测控制基于qp二次优化原理求出最优控制解，在波浪补偿和控制中的预测精度和自适应度主要取决于机械系统传递函数的建立，可以在建立传递函数的环节进行改进，提高系统对非线性系统传递函数的识别能力，从而提高波浪补偿模型预测控制的预测精度和自适应程度.