关于近拟常曲率空间具有常平均曲率超曲面

耿 杰, 宋卫东,2

(1.安徽信息工程学院 通识学院,安徽 芜湖 241000；2.安徽师范大学 数学与统计学院,安徽 芜湖 241000)

引言

设(Nn+p,g)是n+1维单连通完备的黎曼流形,Mn是其紧致的极小子流形,S表示Mn的第二基本形式模长的平方,对于单位球面Sn+p(1),则有著名的J.Simons型积分不等式[1]

(1)

其中*1表示Mn的体积元。不等式(1)对子流形几何的研究和发展产生了重大影响,应用J.Simons方法,建立了Sn+p(1)中各种子流形的J.Simons型积分不等式。于是将J.Simons积分不等式推广到非空间形式自然就成了大家的研究课题。

文献[2]中,Z.G.Bai引入了拟常曲率空间的概念,其黎曼曲率张量KABCD取如下形式：

(2)

其中g为Nn+p的黎曼度量,a,b为Nn+p上的C∞一函数,{λA}为Nn+p上的单位向量函数,并建立了拟常曲率空间的J.Simons积分不等式。

显然,拟常曲率空间是常曲率空间Sn+p(a)的推广。

进一步,U.C.De等人建立了近拟常曲率空间[3],其黎曼曲率张量KABCD,取如下形式：

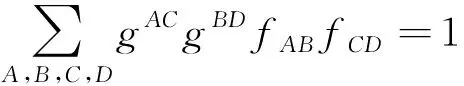
(3)

其中{fAB}为Nn+p上单位向量函数,并给出了一个具体的例子。

显然,近拟常数曲率空间是拟常曲率空间的推广，此时

fAB=λA·λB。

(4)

W.D.Song等建立了拟常曲率空间中具有常平均曲率紧致超曲面关于其第二基本形式模长平方S的J.Simons型积分不等式[4]。本文将这个结果,推广到近拟常曲率空间,具体结果如下：

定理1设Mn是n+p维单连通完备的近拟常曲空间Nn+p中具有常平均曲率紧致超曲面。则有下列积分不等式

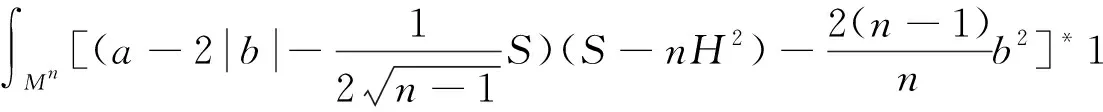
其中S为Mn的第二基本形式模长的平方,H为Mn的平均曲率。

由定理1,有

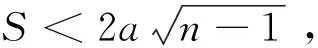
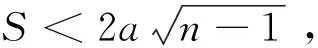
1 一些局部公式

本文对各类指标的取值范围约定如下：

1≤A,B,C,…≤n+1,1≤i,j,k,…≤n。

设Nn+1是n+1维单连通完备的黎曼流形,Mn是Nn+1中紧致超曲面，在Nn+1上选取局部标准正交基{eA},使得它们限制在Mn上,{ei}与Mn相切,于是在此标架下,若Nn+1是近拟常曲率空间,则具黎曼曲率张量为：

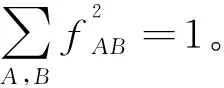
(5)

设{ωA}、{ωAB}分别是{eA}的对偶标架场及联络1-形式,限制在Mn上,有[5]

(6)

(7)

(8)

Rijkl=Kijkl+hikhjl-hilhjk,

(9)

式中h,Rijkl及Kijkl分别是Mn的第二基本形式、曲率张量场及Nn+1的曲率张量场,又Mn的第二基本形式模长的平方S及Mn的平均曲率H分别是

(10)

用hijk、hijkl表示hij的共变导数,则[6]

hijk-hikl=-Kn+1 ijk,

(11)

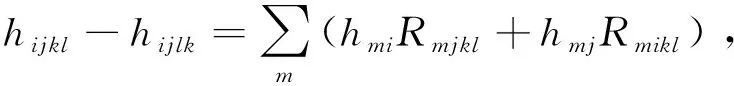
(12)

(13)

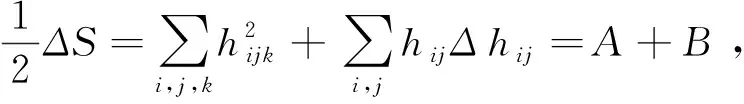
(14)

(15)

(16)

2 定理的证明

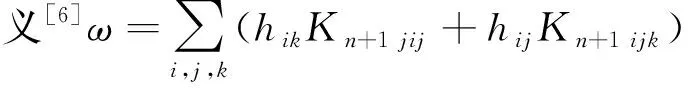
从而

又Mn具有常平均曲率,结合(5)(11)式,有

(17)

(18)

于是

A≥-2(n-1)b2-dω。

(19)

下面估计B,为此,选择Mn的局部标准正交标架场{ei},使得hij=λiδij,令

(20)

从而

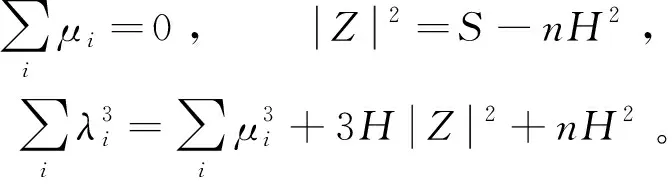
(21)

引理[7]记号如上,对于n>2,有下列不等式

(22)

等号成立当且仅当n-1个μi相等。

因此,由(9)得

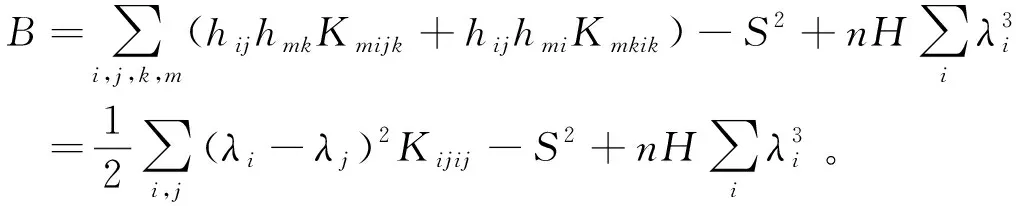
(23)

由(21)(22)得

(24)

由(5)及|fjj|≤1,有

≥n(a-2|b|)|Z|2,

(25)

从而由(23-25)得

(26)

作正交变换

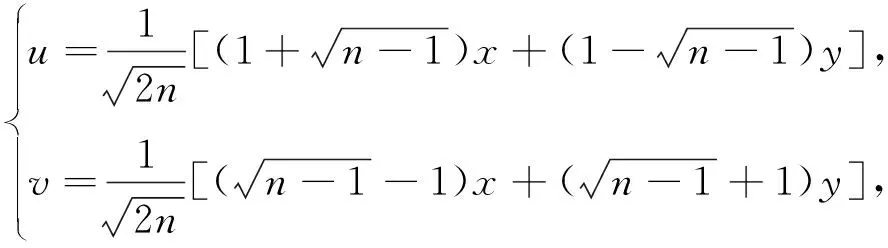
(27)

F(x,y)可以写成

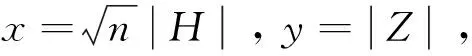
(28)

从而

(29)

于是,由(14)、(19)及(29),即完成定理1的证明。