二年级教学“乘法分配律”的实践与思考

文|吴锐洁

“乘法分配律”的教学在整个小学数学教学中十分重要，承载着重要的数学模型，一般安排在中高年段系统学习，旨在引导学生理解运算律的意义，使一些运算简便，提高运算能力。然而，通过访谈我们发现：学生对乘法分配律的掌握情况却不尽如人意。到底是什么原因导致这种情况的出现呢？大量的文献资料表明：一是模型理解问题，学生着眼于方法的解释“先求什么再求什么”而非方法间算式的内在关系的阐释，导致规律的机械记忆而没有理解规律的内涵本质；二是难点集中问题，五个运算律的系统学习共同奔着“简算”的目的，这种高容量的学习方式造成学生对抽象的运算律的混淆，也导致“乘法分配律”的本质意义和价值得不到充分体现；三是练习指向问题，大量变式练习的过早干扰使学生误入学习乘法分配律就是“为了简算”的怪圈，学生的思维失去了着力点，难以在脑海里将各种“形似而神各异”的习题转化成具有运算律基本结构特点的算式。

能否让学生对“乘法分配律”的认知逐步递加从而分散难点、把握重点呢？查看教学参考书，书中提到运算律的学习第一阶段没有出现“乘法分配律”的概念，是自然渗透、自觉运用阶段，那我们能不能让书中的这个建议更加显性化些呢？查看教材，以北师大版为例，二年级“6～9的乘法口诀”单元中，通过点子图、线段图来说明像“7个6就是5个6加2个6的和”这样的问题，通过“做乘法表”引导学生沟通理解口诀之间的内在联系，探索乘法表规律，这些已经开始渗透乘法分配律了；在三年级学习整数乘法计算方法的过程，事实上也在不断借助点子图法、解释表格法、竖式计算的步骤体会基于乘法分配律的计算道理；此外，在几何领域，三年级学习长方形的周长和面积变化中，也隐含着“乘法分配律”的几何模型。在正式学习“乘法分配律”之前，教材已有多次运用乘法分配律解决问题。

那么，在保持现有教材体系的基础上，如果我们在四年级或三年级学习“乘法分配律”之前做适当的渗透，是不是可以更充分体现“乘法分配律”的本质意义和价值，同时也使学生更好地理解和运用呢？因此，本研究聚焦到二年级开展“乘法分配律”渗透的“纵向同课异构”教学，以探寻学生学习的可能性。

【教学过程】

在教学“乘法口诀”时渗透乘法分配律，借助直观实物模型抽象成点子图模型的“分开看”与“合并看”——意义的“分开说”与“合并说”——算式的“分开算”与“合并算”来实施，教学过程如下：

一、课前小游戏：分开说与合并说

1.男生好，女生好。（这是分开说）→男生女生好。（这是合并说）

2.我爱阅读，我爱运动。→我爱阅读和运动。

3.我左手有3袋苹果，我右手有4袋苹果。→我两只手一共有（3+4）袋苹果。

【设计意图：以生活中“分开说与合并说”的小游戏拉近与学生的距离，紧密联系本节课乘法分配律“分”与“配”的特征，激活学生对乘法分配律的生活经验，激发学生的学习热情。】

二、图式对接：看——说——算

1.实物苹果模型，渗透算律。

（1）观察下面的红苹果和青苹果，并根据图填空。

（2）把图1和图2合在一起成图3，请问：现在一共有多少个苹果？

追问：你是怎么得到16的？8是怎么来的？有几个2？对应的乘法算式怎么写？请你用一句口诀快速计算。

学生在充分交流基础上小结：3个2加5个2得到（3+5）个2，也就是8个2，对应的算式是3×2+5×2=（3+5）×2=8×2，可以用口诀“二八十六”快速地得到结果。

【设计意图：本环节从可视化苹果实物图模型的“分开看”出发走向“合并看”，唤醒学生乘法意义“几个几”的学习经验，生成教学所需，初建模式。通过直观性的模型图使学生建立图式对接，积累可视性学习经验，渗透乘法分配律。】

2.对比延伸模型，丰富算律。

（1）仔细观察下面的苹果图，看图写出几个几、列出算式并写出口诀。

（2）这两幅图有什么联系，你是怎么想的？

请你结合“几个几+几个几”来解释说明，并用一个等式来表示它们之间的关系。

【设计意图：本环节既是对上一环节的巩固，也是对上一环节的延伸，学生在对比观察中发现，有的可以竖着合并，有的可以横着合并，这样的设计让教学内容更具宽度。】

3.抽象点子模型，明晰算律。

请你仔细观察，苹果抽象笑脸，笑脸抽象点子图，这几幅图有什么区别？

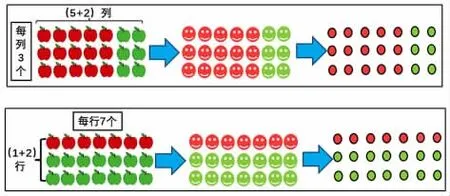
【设计意图：本环节通过实物模型的动态变化，直观形象，过渡到点子图这一半抽象模型的呈现，让学生在对比中厘清不同模型图本质上是一致的，从而在脑海中建立起多元化又相互关联的模型表征，有效积累表象操作，为后续转向符号操作的学习打好基础。】

4.选择模型，深化算律。

（1）请你在图1、2、3中选择两幅图，使它们合并在一起后能用类似3×2+5×2=（3+5）×2=8×2的算式表示。

（2）为什么你不选择图2和图3合并在一起？

（3）图1和图3一定能拼成功吗？

【设计意图：本环节直接选用点子图让学生寻找可合并的模式，关注学生基本活动经验积累的学习，学生在合并摆的过程中逐步明晰模型特征。同时，以反例冲击，为归纳算律埋下伏笔，让教学内容更具深度。】

5.归纳小结，表达算律。

观察算式，你发现了什么？两个分开算的算式，怎样才能拼成一个乘法算式呢？

学生观察算式特点交流后小结：两个分开算的乘法算式，如果有一个相同的乘数，可以合并成一个乘法算式。

【设计意图：在经历知识的形成和发展过程后，自主观察发现算式的特征，采用不完全归纳法小结，并学会用自己的语言表达算律，将内在思维活动外显出来，提高探索数学问题的兴趣。】

6.练习巩固，应用算律。

请你用一句口诀算出下面的算式。

5×7+4×7= 口诀：_______________

9×5+9×2= 口诀：_______________

【设计意图：两道简单的练习对接乘法口诀，探究口诀的内在联系，从乘法意义角度加深对口诀的理解。】

三、全课小结，课后延伸

1.今天我们通过模型图学习了分开算与合并算，你学会了什么？

2.请根据点子图填空。

（1）这是一幅5行9列的点子图，你可以横着或竖着圈一圈，把它分开来研究，并分别写出几个几、列出算式和写出口诀（可以借助框图帮助理解）。

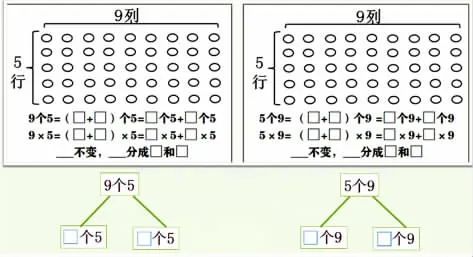
（2）你发现了什么？

归纳：一个乘法算式，可以分开成两个乘法算式再相加，这三个算式中都有一个相同的数。

（3）请你运用“分开算与合并算”的方法计算下列算式，说说你的思考过程。

（9+7）×3= 18×4=

【设计意图：回顾整理“分开→合并”的学习过程，同时以开放式问题的设计进一步深化由“分开→合并”的过程转向“合并→分开”的过程，打破学生的思维定势，拓展学生自主探究的能力，完善对所学内容的理解。】

【分析与思考】

这样的教学，教学效果如何呢？我们针对“学生能根据算式特点用乘法分配律对合并型和分开型算式进行计算吗”做了前测和后测，情况如下：

合并型:前测中正确率达到69.05%，可以看出尽管学生没有乘法分配律的渗透，但是类似于这种题目的解决还是不错的，访谈9人，有1人根据数字特点进行选择，其余8人都是先乘后加得出结果再选择。后测中正确率是90.05%，提高了21%，访谈18人，有12人已经能直接用乘法分配律合并算，超过66.7%的学生能灵活应用乘法分配律进行解答。

分开型：正确率从前测的35.71%提升到后测的51.2%，访谈中发现，前测中学生大致有两种做法：一是拆数法，将13拆成10和3或9和4再分别乘3；二是乘法意义法：3个13相加或13个3先算三九二十七，再连续加4个3。后测中情况有好转，这部分学生几乎都用拆数法结合乘法意义来解释，也就是活学活用“乘法分配律”进行解题。

我们在思考：如果给二年级学生渗透“乘法分配律”这一内容，有何独特的价值？经过实践，我们认为有以下三点：

1.积累了学习乘法分配律的基本活动经验。

借助不同的模型让学生在不同年级多元渗透乘法分配律的意义，从已有的模型如点子图、线段图、面积模型等唤醒学生对知识的直观理解，积累直观的操作活动体验，让学生学得清楚，悟得明白。

2.助力学生对口诀及乘法竖式等的深度理解。

查看教材，二三年级学习了乘法口诀、乘法竖式、长方形周长及面积变化中都隐含着乘法分配律。如果在二年级学习乘法口诀时渗透乘法分配律分与合的意识，沟通知识之间的关联性，一方面探究了口诀之间的内在联系，使口诀的记忆不再割裂，将相邻或不同口诀之间进行链式记忆；另一方面加强了学生对多位数乘法竖式算理的深度理解。

3.逐步感知，分散学习难点。

“乘法分配律”为何成为学生的“负担”？原因之一是难点集中，让“乘法分配律”在不同年级“小步子”螺旋式循序呈现，初识“乘法分配律”淡化其简算的痕迹，避免各种变式训练过早地把学生的视线引向简算从而导致各种混淆和模糊不清，加深学生对“乘法分配律”的多维度理解，尤其是意义理解，分散其学习难点，保证学习内容的连续性，使学生逐步掌握。

通过教学实践研究，我们认为在二年级学习乘法口诀时注重知识的整体性，有意识地渗透乘法分配律是有可能的。如果学习乘法口诀时只是一味地让学生花更多的时间来背口诀，而非从乘法意义上探究口诀的内在联系，将导致高年级学生对乘法分配律的学习与理解出现障碍。