让静止的图形动起来
——《滚动中的圆》教学设计与意图
文|章恺欣 吴玉兰
在《圆的周长与面积》单元学习结束时,对一个班40名学生进行了测查,其中“已知圆的面积是12.56cm2,求圆的周长”这一题,只有3人不能正确解答;而“一个直径为1cm的圆,绕着长是5cm,宽是3cm的长方形外侧无滑动地滚动一周,求圆心经过的路线长度”这一题,仅有4人能正确解答。可见,学生已熟练掌握圆周长与面积计算的基本公式,能正确解答静止状态下圆的周长与面积的相关问题。但当图形运动变化后,学生就很难建立运动前后图形的方位和相互的位置关系,想象图形的动态变化过程成了学生解决问题中的一大难点。
如果能将静止的图形动起来,是否能降低学生思考的难度,搭建学习的桥梁?是否利于学生积累活动经验,培养空间观念?于是,我们进行了尝试,将圆绕多边形外侧无滑动滚动的问题汇总成一节数学思维拓展课,借助微课动态呈现圆的运动过程,将空间想象与动态操作相结合,力图培养学生的空间观念和推理能力,积累活动经验。
【教学过程】
一、运动中引入,奠定基础
1.开门见山,揭示课题。
师:今天我们一起来研究滚动中的圆。(板书课题)
2.出示线段OA。
师:这儿有一条线段,如果把它绕着定点O旋转一周,会形成什么图形?
生:圆或圆面。
师:(几何画板演示)确实,动点A经过的轨迹是一个圆,线段OA运动后会形成一个圆面。
【设计意图:本环节从简单的线段的运动引入,让学生初步体会点与线运动后会形成新的图形,为后续的研究奠定基础。同时,先想象,再动态展示变化过程,利于培养学生的空间想象能力。】
二、操作中探究,突破难点
1.想象圆沿直线滚动。
提出问题:还是这个圆,如果沿着这条直线向前滚动,想象一下,圆心A经过的路线会是怎样的,能用手比划一下吗?如果圆滚动了一周,那么圆心经过的路线会有多长呢?

在学生比划的基础上用课件动画演示圆滚动的过程,得出“圆心经过的长度=圆的周长”。
2.探究圆沿长方形外侧滚动。
(1)提出问题。
师:如果这个圆沿着长方形的外侧滚动一周,圆心经过的路线会怎样?
(2)独立研究。
师:老师为大家准备了四份不同的学习任务,分别是智慧卡A、B、C、D。
活动建议:
①先看智慧“A卡”,如果还有困难,可以看“B卡”,以此类推。
②选择一张适合自己的智慧卡进行研究,智慧A、B、C卡任务相同。
学习任务:
如图所示,一个直径为1cm的圆,绕着长是5cm,宽是3cm的长方形外侧无滑动地滚动一周。
任务1:画出圆心经过的路线。想一想,圆心经过拐角时,会形成怎样的路线呢?
任务2:试着求出圆心经过的路线长度。
智慧D卡将任务1调整为:画出圆心经过的路线。想一想,圆心经过拐角时,会形成怎样的路线呢?可以先用材料包中的小圆片摆一摆,滚一滚,再画一画。
不同层次的智慧卡提供了不同的配图,分别如下:

智慧A卡

智慧B卡

智慧C卡、D卡
(学生选择适合自己的学习任务卡进行独立研究)
(3)四人小组交流。
交流建议:选D卡的先说,然后按C、B、A卡的顺序进行补充;推选一人准备汇报。
(4)全班交流。
师:哪个组愿意上来与大家分享你们的研究成果?
生:我们觉得圆心经过的路线的长度是一个大长方形的周长。这个大长方形长5+1=6cm,宽3+1=4cm,周长是(6+4)×2=20cm。所以圆心经过的路线长度是20cm。

生:我们组有不同的想法。我们觉得圆在长方形顶点处滚动时,圆心经过的路线不是直的,是有弧度的,像这样。所以圆心经过的路线应该是原来长方形的周长再加上一个直径为1cm的圆的周长。

师:看来目前大家有两种不同的想法,到底哪种是对的呢?
师:请两方的支持者各自说自己的理由,并请选择智慧D卡的学生用小圆片演示圆在顶点处的滚动过程,其他同学想象圆心经过的轨迹是怎样的。
师:刚才大家都想象了圆心经过的路线,争议最大的就是圆在长方形顶点处无滑动滚动时到底会形成怎样的路线。接下来,我们就一起来看一段微课,看看正确的路线到底是怎样的。
(播放微课,微课里动态展示圆的运动过程,并结合运动过程显示圆心经过的轨迹。同时通过与原来长方形的比较以及四个扇形的剪拼,发现“圆心经过的路径的长度=长方形的周长+圆的周长”)
【设计意图:在前期的测查中发现全班40名学生中,只有4人能正确解答圆沿长方形一周无滑动滚动的问题。在不能正确解答的36人中,有6人能正确画出运动轨迹,但计算错误;有23人尝试画出轨迹,但不能正确描画圆心在长方形顶点处的运动轨迹;剩余的7人画不出轨迹,没有任何解决问题的方法。可见,面对同一个问题,学生有着不同的学习基础与能力。因此,本环节借助“分层智慧卡”为学生提供了不同提示的图示,并为学习能力最弱的学生提供了圆片,使他们能借助操作想象运动过程。“分层智慧卡”的设置,为不同层次的学生提供个性化的帮助,使每一层次的学生都能借助“分层智慧卡”独立研究并获得成功。
自主研究后,本环节还安排了交流过程,呈现学生不同的研究成果。在双方辨析的基础上播放微课,动态演示运动过程,呈现运动轨迹。这样的处理,使学生先经历想象、审辩的过程,再借助微课,使静态的图形动起来,很好地建立了图形运动前后相互的位置关系,更利于学生高阶思维与空间观念的培养。】
三、猜测后验证,得出规律
1.初次研究,提出猜想。
师:刚才小圆沿着长方形外侧滚动一周,圆心经过的路线长度等于长方形的周长加上圆的周长。那如果沿着三角形、五边形的外侧无滑动滚动,圆心经过的路线长度又会有多长?
(学生提出各种猜想)
2.再次研究,发现规律。
(1)独立研究。
研究建议:同桌分工,一人研究一个图形;画一画、算一算,有困难可以动手滚一滚;完成后可以向同桌介绍研究成果。
(2)全班交流。
生:我研究的是圆沿三角形外侧无滑动滚动,路线是这样的。我发现圆心经过的路线是“圆的周长+三角形的周长”。

生:我研究的是圆沿五边形外侧无滑动滚动,路线是这样的,我发现圆心经过的路线是“圆的周长+五边形的周长”。

(3)验证。
播放微课,验证研究结果是否正确。以下是微课中的部分画面。
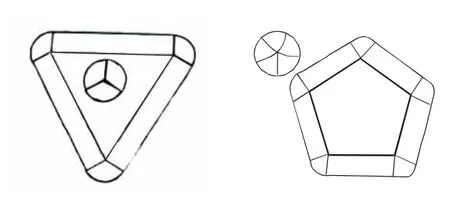
(4)质疑。
师:看完微课,大家还有什么要问的吗?
生:微课里几个扇形拼在一起看上去正好是一个圆。是不是真的是一个圆?会不会有误差?
生:如果不拼,能验证剩下的几个扇形合在一起是一个圆吗?
师:有人能解决吗?
生:来看我画的这幅图。

生:这是一个周角,等边三角形的每个内角都是60°。360°-60°=300°,再去掉边上两个长方形的两个直角,300°-90°×2=120°。所以每个扇形圆心角都是120°,120°×3=360°,正好可以拼成一个圆。
(五边形研究过程略)
小结:小圆沿着长方形、等边三角形和五边形外侧无滑动滚动一周,圆心经过的路线长度都是圆的周长加里面图形的周长。
3.应用规律,进行推理。
师:如果沿六边形、七边形等的外侧无滑动滚动,圆心经过的长度又会是怎样的?现在你有什么想说的?
生:圆沿任意多边形外侧无滑动滚动,圆心经过的路线长度=圆的周长+任意多边形的周长。
【设计意图:在突破了“圆心在图形顶点处滚动时的路线”这一难点后,本环节设计了圆沿任意多边形外侧无滑动滚动的研究,从简单的长方形,逐步走向三角形、五边形以及其他多边形,从特殊逐渐走向一般,引导学生经历“想象猜测、操作验证、归纳发现”的过程,体会数学思想。同时,从“想象、画路线”“微课动态操作”逐步走向用数学的方法说理,提升学生用数学知识解释、说明问题的能力,培养学生的高阶思维。这样的“想-做-想”的过程,也利于学生空间观念的培养。】
四、梳理中小结,练习提升
提出新问题:研究到这儿,你有什么想说的?你还有什么想研究的?
生:我还想研究圆在图形内部滚动,圆心经过的路线是不是也会有规律。
生:我还想研究圆在图形内部或外部滚动时,扫过的面积是怎样的。
指明后续研究方向:运动中的圆还有很多值得我们研究的地方,有兴趣的同学课后也可以像今天这样,想一想,画一画,遇到困难也可以动手做一做,看看是否存在规律。
【设计意图:本课的最后,让学生继续提出还想研究的问题,将学习内容进行了延伸,从圆在图形外侧的滚动走向图形内侧的滚动,从周长的研究走向面积的探索,激发学生继续探究的欲望。同时,教师小结中的“想一想,画一画,做一做”,也是学习方法的梳理,为后续研究奠定基础。】

