对称及反对称矩阵空间的保持逆矩阵的函数

樊玉环，袁海燕，魏 喆

(黑龙江工程学院 理学院，哈尔滨 150010)

定义在域到域自身的函数，若矩阵经函数后所得新矩阵的秩等于原矩阵的秩，则称函数是保秩的.例如文献[1]给出了连续函数保秩的充要条件是函数是线性函数，文献[2]给出了完整的保所有矩阵秩的函数形式，文献[3]给出了大于等于2阶矩阵保秩的函数的形式；函数保持的基本思想之一是改变已有函数所作用的集合，例如文献[4]研究保秩的函数从文献[1-3]中的全矩阵空间改变成对称矩阵、反对称矩阵及上三角矩阵空间上的保秩的函数的形式；函数保持的基本思想还有寻求新的不变量.例如文献[4]中引入了新的不变量保行列式、保伴随、保幂等，若矩阵经函数后所得新矩阵的行列式等于原矩阵的行列式，则称函数是保行列式的；若有两个矩阵，其中一个是另外一个的伴随矩阵，经函数后所得两个矩阵仍是一个矩阵是另一个矩阵的伴随矩阵，则称函数是保伴随的；若满足一个幂等(幂零)矩阵经过函数后所得的新矩阵仍是幂等(幂零)矩阵，则称此函数是域上保幂等(幂零)的函数；文献[4]给出了全矩阵空间上保行列式、保伴随及保幂等的函数形式；根据函数保持的基本思想，文献[5]给出了上三角矩阵空间上的保持幂等矩阵的函数的形式，但其他特殊的矩阵空间，例如对称矩阵空间、反对称矩阵空间等上的保幂等的函数还有待于进一步研究；文献[6]给出了特殊矩阵空间上的保行列式的函数形式；文献[7-9]则是寻求了新的不变量.在文献[10-12]中研究了可逆矩阵的性质及其求法.本文是在文献[9]的基础上研究了对称矩阵空间及反对称矩阵空间上的保持逆矩阵的函数的形式.

1 符号及基本概念

设F是特征不为2的域,F*表示F/{0},Sn(F)为F上所有n阶对称矩阵的全体,SKn(F)为F上所有n阶上反对称矩阵的全体,E为单位矩阵，A=(aij)，Af=(f(aij))，AT为A的转置矩阵.

定义1.1[13]设n阶矩阵A=(aij)n×n，若存在n阶矩阵B，满足AB=BA=E，称B为A的逆矩阵.

定义1.2[13]若矩阵A=(aij)n×n满足A=AT，则称A为对称矩阵.

定义1.3 若矩阵A=(aij)n×n满足AT=-A，则称A为反对称矩阵.

定义1.5[14-15]若f:F→F满足f(a+b)=f(a)+f(b),f(ab)=f(a)f(b).则称f:F→F是同态.

2 对称矩阵空间上保逆矩阵的函数

定理2.1f是n(n≥3)阶对称矩阵空间上的保持逆矩阵的函数充要条件是f=cδ，其中c是1或者-1，δ是域F上的满足δ(1)=1单自同态.

证明先证明充分性

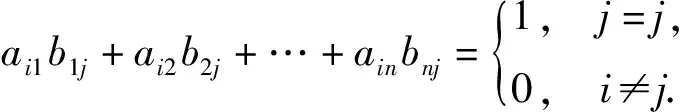
由f的定义，可知AfBf的(i,j)元为

f(ai1)f(b1j)+f(ai2)f(b2j)+…+f(ain)f(bnj)

若f=δ，由δ的定义知

f(ai1)f(b1j)+f(ai2)f(b2j)+…+f(ain)f(bnj)=

δ(ai1)δ(b1j)+δ(ai2)δ(b2j)+…+δ(ain)δ(bnj)=

若f=-δ，由δ的定义知

f(ai1)f(b1j)+f(ai2)f(b2j)+…+f(ain)f(bnj)=

(-δ(ai1))(-δ(b1j))+(-δ(ai2))(-δ(b2j))+

…+(-δ(ain))(-δ(bnj))=

δ(ai1)δ(b1j)+δ(ai2)δ(b2j)+…+δ(ain)δ(bnj)=

下面证明必要性

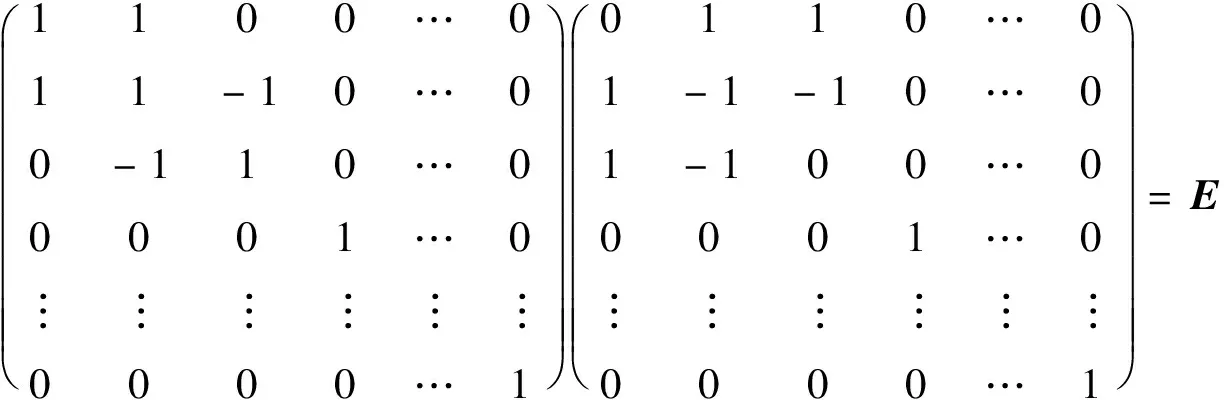
由Af,f的定义，可知

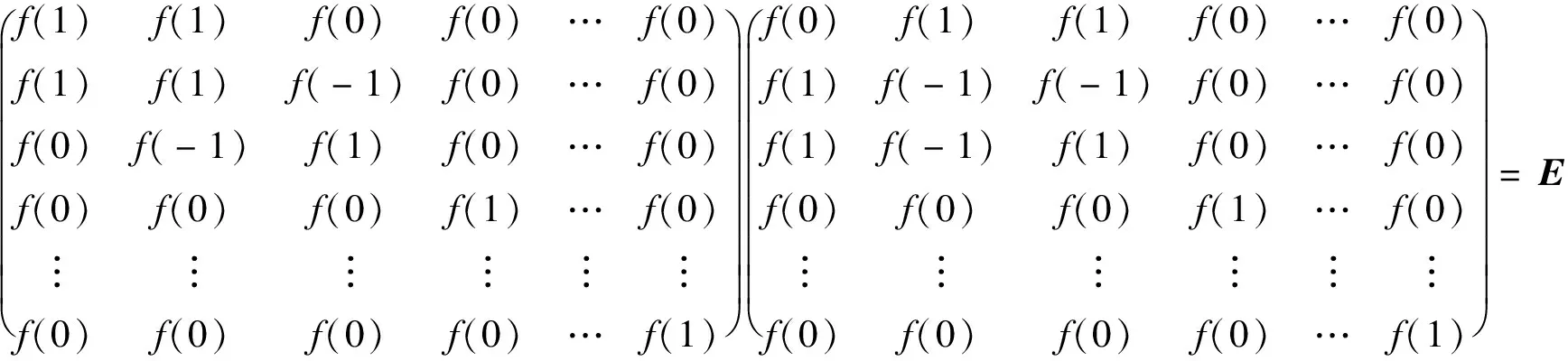
f2(1)+2f(1)f(0)+(n-3)f2(0)=1

(1)

f2(1)+f(1)f(-1)+f(0)f(-1)+(n-3)f2(0)=0

(2)

f2(1)+f(1)f(-1)+(n-2)f2(0)=0

(3)

f2(1)+f(1)f(0)+f(1)f(-1)+(n-3)f2(0)=0

(4)

f2(1)+f2(-1)+f(1)f(-1)+(n-3)f2(0)=0

(5)

f2(-1)+2f(1)f(0)+(n-3)f2(0)=1

(6)

由式(1)、(6)可知

f2(1)=f2(-1)

(7)

由式(2)、(4)可知

f(1)f(0)=f(-1)f(0)

(8)

由式(4)、(5)可知

f2(-1)-f(1)f(0)=1

(9)

由式(2)、(3)可知

f2(0)=f(-1)f(0)

(10)

由式(5)、(6)可知

f2(1)+f(1)f(-1)=2f(1)f(0)

(11)

由式(7)可知f(1)=±f(-1)，若f(1)=f(-1)，则由式(9)可知f(1)(f(1)-f(0))=1可得f(1)≠0,且f(1)≠f(0).再由式(11)可知f2(1)=f(0)f(1)，由f(1)≠0可得f(1)=f(0).产生矛盾，所以f(1)=f(-1)这种情况不成立，故

f(1)=-f(-1)

(12)

由式(8)、(12)可得

f(0)=0

(13)

由式(9)、(13)可得

f2(-1)=1

(14)

(15)

由Af,f的定义及式(13)可得

(16)

f(a)=-f(-a)

(17)

由Af,f的定义及式(13)可得

f(1)f(1)+f(1+a)f(-1)+f(a)f(1)=0

(18)

再利用式(15)、(17)可得

f(1)+f(a)=f(1+a)

(19)

由Af,f的定义式(13)、(17)可得

(20)

利用式(15)可得

f(1)f(ab)=f(a)f(b)

(21)

下面证明δ是域F上的满足δ(1)=1单自同态.

由式(14)、(17)可知f2(1)=1

当f(1)=1时，令δ=f

应用式(21)得

δ(ab)=f(ab)=f(1)f(ab)=

f(a)f(b)=δ(a)δ(b)

即

δ(ab)=δ(a)δ(b)

(22)

应用式(19)、(22)得

f(a)+f(b)=δ(a)+δ(b)

即

δ(a+b)=δ(a)+δ(b)

(23)

当f(1)=-1时，令δ=-f

应用式(21)得

δ(ab)=-f(ab)=f(1)f(ab)=

f(a)f(b)=δ(a)δ(b)

即

δ(ab)=δ(a)δ(b)

(25)

应用式(19)、(25)得

-f(a)-f(b)=δ(a)+δ(b)

即

δ(a+b)=δ(a)+δ(b)

(26)

由以上证明可知无论哪种情况，δ都是域F上的自同态.

由式(15)可得

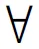
(27)

若δ(a)=δ(b)，则f(a)=f(b)，f(a)-f(b)=0，应用式(17)f(a)+f(-b)=0，即δ(a)+δ(-b)=0，应用式(23)或式(26)δ(a-b)=0，即f(a-b)=0，应用式(27)得a=b.从而δ是域F上的单自同态.

在情况1中，δ(1)=f(1)=1，在情况2中，δ(1)=-f(1)=1，总之无论哪种情况，δ(1)=1从而f是n阶对称矩阵空间的保持逆矩阵的函数一定能得到f=cδ，δ是域F上的满足δ(1)=1单自同态.

定理2.2f是二阶对称矩阵空间上的保持逆矩阵的函数充要条件是f=f(1)δ，其中δ是域F上的单自同态.

证明充分性显然，下面证明必要性.

f(1)f(0)=0

(28)

f2(1)+f2(0)=1

(29)

这与f是二阶对称矩阵空间上的保持逆矩阵的定义矛盾，所以f(1)=0不成立，即有

f(0)=0

(30)

f2(1)=1

(31)

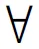
(32)

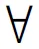
f(-a)=-f(a)

(33)

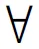
f(1)f(ab)=f(a)f(b)

(34)

f(b+1)=f(b)+f(1)

(35)

令δ=f-1(1)f，类似于定理2.1中的证明可得δ是域F上的单自同态.

3 反对称矩阵空间上保逆矩阵的函数

定理3.1f是四阶反对称矩阵空间上的保持逆矩阵的函数充要条件是f=f-1(1)δ，其中δ是域F上的满足δ(1)=1单自同态.

证明先证明充分性

记aij=-aij,bij=-bji(i≠j),aii=bii=0

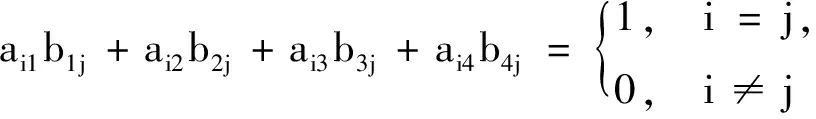
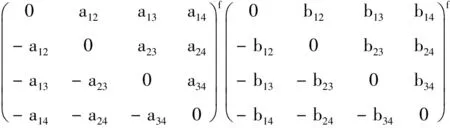
f(ai1)f(b1j)+f(ai2)f(b2j)+f(ai3)f(b3j)+f(ai4)f(b4j)，且1=δ(1)=f(1)/f-1(1)=f2(1)，故

f(ai1)f(b1j)+f(ai2)f(b2j)+f(ai3)f(b3j)+f(ai4)f(b4j)=

f2(1)f(ai1)f(b1j)+f2(1)f(ai2)f(b2j)+f2(1)f(ai3)f(b3j)+f2(1)f(ai4)f(b4j)=

δ(ai1)δ(b1j)+δ(ai2)δ(b2j)+δ(ai3)δ(b3j)+δ(ai4)δ(b4j)

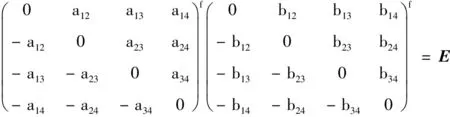
说明若f=f-1(1)δ，其中δ是域F上的满足δ(1)=1单自同态，则f是四阶反对称矩阵空间的保持逆矩阵的函数.

下面证明必要性

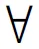
由Af的定义及Af∈SK4(F)可知

f(0)=0

(36)

f(-a)=-f(a)

(37)

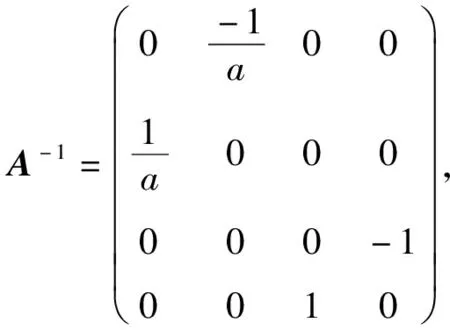
(38)

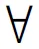
根据Af、f的定义及式(36)、(37)可知

f(1)f(2)+f(x)f(1)-f(1+x)f(1)=1

(39)

(40)

在式(38)中令a=1，可得

f2(1)=1且f(1)≠0

(41)

则式(39)可化成

f(1)f(2)+f(x)f(1)-f(1+x)f(1)=f2(1)

两边同时除以f(1)，可得

f(2)+f(x)-f(1+x)=f(1)

(42)

在式(42)中令x=0，利用式(1)，得到f(2)=2f(1)，将其带入式(42)

f(1)+f(x)=f(1+x)

(43)

f(1)f(ty)=f(y)f(t)

(44)

下面令f(x)=f-1(1)δ(x)，利用定理2.1中的证明方法可知δ是域F上的满足且δ(1)=1单自同态.

对于任意的大于四阶的反对称矩阵，在选取过程中，从第五行开始可取紧贴主对角线两边的元素为1和-1，其他为0，例如六阶时可取

因为书写时比较复杂，所以以四阶反对称空间证明，当然任意大于四阶的偶数阶反对称矩阵空间仍有同样结论.

定理3.2f是大于等于四阶的偶数阶反对称矩阵空间的保持逆矩阵的函数充要条件是f=f-1(1)δ，其中δ是域F上的满足δ(1)=1单自同态.

定理3.3f是二阶反对称矩阵空间的保持逆矩阵的函数充要条件是f是满足f(x)f(y)=1(若xy=1)的域F上的单自同态.

4 结 语

本文刻画出了对称矩阵上保持逆矩阵的函数的形式；给出了偶数阶反对称矩阵上的保持逆矩阵的函数的形式.本文的结果是在特征不为2的域上研究的，特征为2的域上的情况还需进一步研究；反对称矩阵空间上保逆矩阵的函数只给出偶数阶的情况，奇数阶的情况还需研究.本研究丰富了函数保持问题的成果.