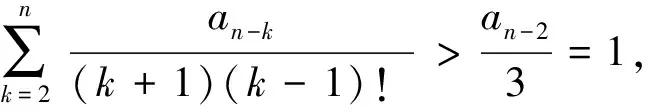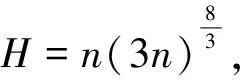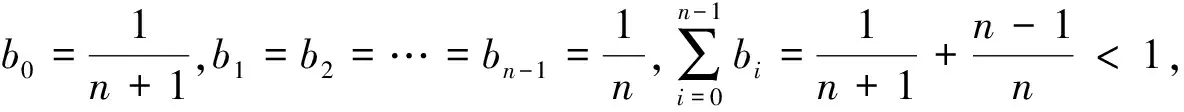一类n阶完全边值问题正解的存在性
邓瑞娟
芜湖职业技术学院基础部,安徽芜湖,241003
近几十年来,常微分方程边值问题在力学、电磁学、生物学等众多领域有着广泛应用,引起了学者们的关注,关于其理论和应用的研究也得出了许多有意义的结论[1-8]。如文[3]利用了锥上的不动点理论讨论了在超线性或次线性增长条件下三阶两点边值问题:
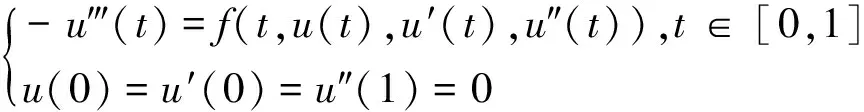
(1)
正解的存在性。
除了对二阶、三阶等边值问题的研究外,也有学者研究更一般的n阶情形。如文[7]研究了在非线性项f(t,x0,x1,…,xn-1)关于xi(i=0,1,2,…,n-1)具超线性增长条件时n阶两点边值问题:
(2)
解的存在性结果。
然而,关于n阶两点边值问题(2)在f满足次线性增长条件时的情形未见有人研究,本文在文[3]的基础上,运用锥上不动理论研究这一问题,并给出正解的存在性结果。
1 预备知识
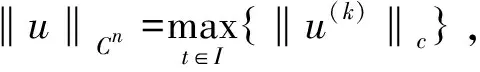
为进一步讨论非线性BVP(2)正解的存在性,先考虑形如(3)的线性微分方程(LBVP),即BVP(2)对应的LBVP,其中h∈C+(I),
(3)
引理1对于∀h∈C+(I),LBVP(3)有唯一解u:=Sh∈Cn(I),且解算子S:C(I)→Cn-1(I)是线性全连续算子。
证明对于∀h∈C+(I),易知LBVP(3)有唯一解u(t),且u(t)可用如下式子表示
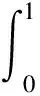
(4)
其中G(t,s)满足
(5)
为对应的格林函数。另由(4)和(5)式可得,解算子S:C(I)→Cn-1(I)为有界线性算子。因为嵌入映射Cn-1(I)→Cn-2(I)是紧的,所以S:C(I)→Cn-1(I)是线性全连续算子。
引理2设h∈C+(I),则LBVP(3)的解u=Sh具有如下性质
(1)对∀t∈[0,1],有u(k)(t)≥0,u(n)(t)≤0,k=0,1,2,…,n-1;
(2)‖u(k)‖C=u(k)(1),‖u(n-1)‖C
=u(n-1)(0),k=0,1,2,…,n-2;
(4)‖u‖C≤‖u′‖C≤…≤‖u(n-1)‖C,‖u‖Cn-1=‖u(n-1)‖C。
证明(1)取h∈C+(I),u=Sh为LBVP(3)的解,由(4)式可知,当k≤n-1,k∈时有下式成立,
(6)
同时,由(5)式可得:
(7)
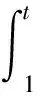
(2)由u(t)及其各阶导数的符号,易知u(k)(t)(k=0,1,2,…,n-2)为I上的单调递增函数,u(n-1)(t)为I上的单调递减函数,同时有如下结论成立:
‖u(k)‖C=u(k)(1),k=0,1,2,…,n-2,
‖u(n-1)‖C=u(n-1)(0)。
(3)由(7)式可知,当k=n-2时有
于是有
(8)
结合(6)式,对于任意t∈[0,1],都有
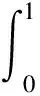
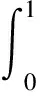
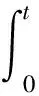
…
综上所述,有如下公式成立
(4)对于任意t∈I,可得
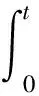

‖u‖C≤‖u′‖C≤‖u″‖C≤…≤‖u(n-1)‖C,同时可得出‖u‖Cn-1=‖u(n-1)‖C。证毕。
为了运用锥上的不动点理论,在Cn-1(I)中,结合引理2中结论(3),用如下方式定义闭凸锥K
u(n-1)(t)≥0,∀t∈I,k=2,3,…,n}
(9)
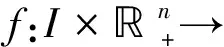
F(u(t)):=f(t,u(t),u′(t),…,u(n-1)(t)),t∈I
(10)
则F将有界集映射为有界集。同时,定义映射A:K→K,A=S°F。

2 主要结果及证明
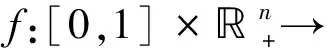
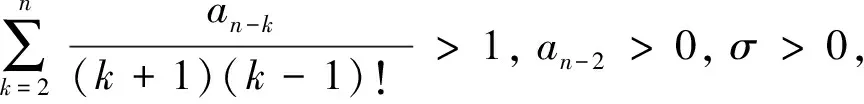
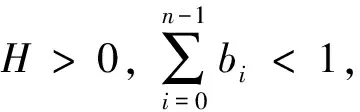
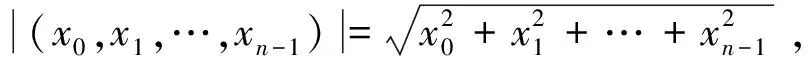
证明取E=Cn-1(I)是一个Banach空间,显然由(9)式定义的闭凸锥K满足K⊂E,A=S°F是由K映射到K的全连续算子。记0 Ω1={u∈Cn-1(I)|‖u‖Cn-1 Ω2={u∈Cn-1(I)|‖u‖Cn-1 (11) 取m∈(0,σ),其中σ>0。令A=S°F,易知A:K→K为全连续算子。取e=S(1),满足对于θ∈Ω1,有e∈K{θ}。下面用反证法证明对于∀u∈K∩∂Ω1,α≥0,都有 u-Au≠αe (12) 假设(12)式不成立,即存在u0∈K∩∂Ω1,α1≥0,使得u0-Au0=α1e。于是可得u0=Au0+α1e=S(F(u0(t))+α1),由S的定义可知,u0是F(u0)+α1∈C+(I)对应的线性边值问题(3)的唯一解。因此,u0∈Cn(I)满足 (13) 综合运用(6)(8)和(11)式,可得如下不等式: i(A,K∩Ω1,K)=0。 下用反证法证明,对于0<β≤1,u∈K∩∂Ω2,映射A满足: βAu≠u (14) 假设(14)式不成立,即存在u1∈K∩∂Ω2,有0<β1≤1,使得β1Au1=u1。于是有u1=S(β1F(u1)),由S的定义可知,u1是h=β1F(u1)∈C+(I)对应的线性边值问题(3)的唯一解。因此,u1∈Cn(I),且满足 (15) ≤(b0+b1+…+bn-1)‖u1‖Cn-1,t∈I。 对上述不等式两端从0到1进行积分,左端可得 于是 i(A,K∩Ω2,K)=1。 综上所述,不动点指数满足 考虑如下完全n阶BVP (16) 此时,an-2=3,an-k=1(k=3,4,…,n),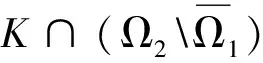
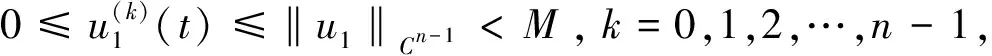
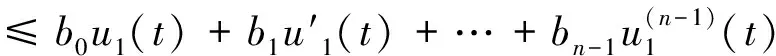
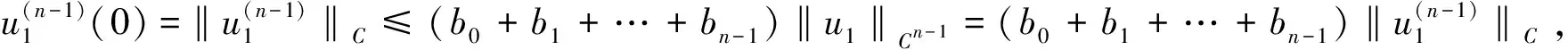

3 应用举例