最大可删除项集快速挖掘算法

赵群礼，郭玉堂

合肥师范学院计算机学院，安徽合肥，230061

挖掘可删除项集(Erasable Itemset)是Deng等人在2009年提出的[1]，用于解决在企业资金紧张的情况下，停产哪些产品损失的利润较小，并据此制定新的产品计划。在此基础上国内外多位学者提出了多种挖掘可删除项集的算法，比如Deng等人在先后提出了VME[2]算法、MERIT[3]算法，Le等[4]在2014年提出了MEI算法，这些算法都能在产品数据库中有效挖掘可删除项集。但是当阈值较大时，这些算法在挖掘过程中都会产生大量的项目集，占用了较大的内存空间和CPU计算时间。为了减少挖掘过程中产生的项目集的数量，节约占用的存储空间，Deng等[5]在2013年提出了挖掘Top-rank-k可删除项集的VM算法；Nguyen等[6]在2015年提出了挖掘可删除闭项集的MECP算法，Vo等[7]在2017年提出了基于约束的挖掘算法pMEIC；Nguyen等[8]在2019年提出了挖掘最大可删除项集的GenMax-EI、Flag-GenMax-EI和PE-GenMax-EI算法。这些算法都能有效解决可删除项集的挖掘问题，而且挖掘的项目集数量都相对较少。但相比较而言，挖掘最大可删除项集的算法产生的项目集更少[8]。另外，由于最大可删除项集的所有子集都是可删除项集，因此，在实际应用中可以将挖掘可删除项集问题转化为挖掘最大可删除项集问题，以减少挖掘过程中的计算量和存储空间。

目前，挖掘最大可删除项集的最新算法主要是Nguyen等人在文献[8]中提出的三个算法：GenMax-EI、Flag-GenMax-EI和PE-GenMax-EI，其中PE-GenMax-EI算法的效率最好。PE-GenMax-EI算法采用了GenMax算法的思想，虽然在挖掘过程中也采用了剪枝技术，但该算法采用按层搜索的方式，在搜索过程中产生了大量的候选项目集，每个候选项集都需要计算收益值，浪费了大量CPU的计算时间和内存空间。本文在现有研究成果的基础上提出了一种新的最大可删除项集挖掘算法MMEIA(Mining Maximal Erasable Itemsets Algorithm)，该算法采用深度优先的搜索方式，利用每个项目对应产品集之间的关系和剪枝策略，使挖掘最大可删除项集的搜索空间更小，产生的候选项集更少，花费的计算量更低。从实验结果可以看出，本文提出的MMEIA算法具有更好的挖掘效率。

1 相关理论

1.1 可删除项集和最大可删除项集

设产品数据库PDB表示为{P1,P2,…,Pm}，Pi为一种产品，该产品中包含的项目表示为Pi.items，该产品具有的价值用Pi.Val表示，数据库的大小表示为|PDB|。设I为PDB中项目的集合，表示为I={i1,i2,…in}，Pi可以表示为{ik1,ik2,…,ikx|ki∈[1…n]}，如表1所示。对于某个项目集S，S⊆I，S的价值表示为Gain(S)，可以用PDB中产品的价值来计算，公式如下：

表1 产品数据库PDB

(1)

例如,项目集S={i6,i7,i8}，Gain(S) =P7.Val+P8.Val+P9.Val+P10.Val+P11.Val= 250 + 150 + 100 + 200 + 150 = 850。

定义1设PDB中所有产品的价值总和用Sum(PDB)表示，δ为设定的阈值，若S满足如下条件：

Gain(S)≤Sum(PDB)×δ

则称S为可删除项集，表示为EI(ErasableItemsets)。

定义2设T是PDB中所有可删除项集的集合，S∈T，若S不是T中任意项集的子集，则称S为最大可删除项集，表示为MaxEI(Maximal Erasable Itemsets)，最大可删除项集的集合表示为MES(Maximal Erasable Set)。

根据定义1和2，可以计算出表1的产品数据库在δ=15%时的可删除项集和最大可删除项集，如表2所示。从表中所列的挖掘结果可以看出，挖掘的最大可删除项集的数量要远少于可删除项集的数量。

表2 δ=15%的可删除项集和最大可删项除

性质1可删除项集中只包含可删除项目，不会包含非可删除项目。

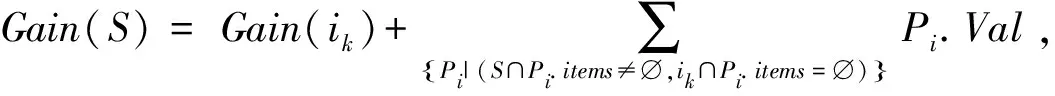
性质2最大可删除项集的所有子集都是可删除项集。

证明根据最大可删除项集的定义可知，其所有子集必为可删除项集，故证略。

推论1若X为最大可删除项集Y的子集，则Gain(X)≤Gain(Y)。

证明假设计算Gain(X)的产品集合为{Pi,Pj,…，Pm}，计算Gain(Y)的产品集合为{Pc,Pd,…，Pi,Pj,…，Pn}，由于X⊆Y，所以{Pi,Pj,…，Pm}⊆{Pc,Pd,…，Pi,Pj,…，Pn}，根据公式(1)，Gain(X)≤Gain(Y)，推论成立，证毕。

1.2 产品集

设ik为PDB中的某个项目，则在PDB中包含ik的所有产品的集合为{Pk1,Pk2,……,Pkm|ik∈Pki.items,1≤ki≤|PDB|}，简称ik的产品集，用P(ik)表示。为了表示方便，产品集中的每个产品都用该产品的id表示，例如在表1中包含i4的产品集为P(i4)={7,8,9}。

(2)

例如,在表1中项集{i4,i5}对应的产品集为：P(i4)∪P(i5)={7,8,9}∪{4,5,6,7,8}={4,5,6,7,8,9}，其收益是P4,P5,P6,P7,P8,P9的价值之和。

性质3设X和Y为两个项目集，它们的产品集为P(X)和P(Y)，则P(XY)=P(X)∪P(Y)。

证明根据项目集对应产品集的定义和示例，可知该性质必然成立，故证略。

推论2若AX和AY为两个项目集，它们具有相同的前缀A，P(AX)和P(AY)分别是它们的产品集，则P(AXY)=P(AX)∪P(AY)。

1.3 产品集之间的包含关系

根据2.2中产品集的定义，若P(X)⊆P(Y)，则X的产品集包含于Y的产品集中，这种包含关系定义如下：

近年来，受哥伦比亚建筑工艺的影响，同时引进了瓜多竹等竹种，墨西哥正在开发更为先进的原竹建筑，但整体的竹建筑行业仍然较为落后。目前，墨西哥至少有4个为建筑配送竹材的中心，同时为竹建筑的开发提供技术支持。这为建筑师和工程师了解竹材用做建材的良好性能提供了便利[11]。

C(Y) = {X|X∈I,P(X)⊆P(Y)}

例如,在表1中，P(i4)= {7,8,9}，P(i6)= {7,8,9,10,11}，P(i7)= {7}，P(i8)= {8,10}，由于P(i4)⊆P(i6)，P(i7)⊆P(i6)，P(i8)⊆P(i6)，可得C(i6)={i4,i7,i8}，同理可得C(i4)={i7}。

性质4对于项目集X、Y、Z，若X∈C(Y)，Y∈C(Z)，则X∈C(Z)。

证明由于X∈C(Y)、Y∈C(Z)，可知P(X)⊆P(Y)，P(Y)⊆P(Z)，由此得到P(X)⊆P(Z)，根据包含关系的定义可得X∈C(Z)，此性质成立，证毕。

2 MMEIA算法

2.1 算法思想

设L1为所有可删除项目的集合，用一维数组表示，L1中的第i个元素表示为L1[i]，其中包含的可删除项目表示为L1[i].items，该项目对应的产品集用L1[i].P表示，项目的收益放入L1[i].val中，L1中的各元素按照每个项目对应产品集由大到小的顺序排列，L1中包含的可删除项目个数用|L1|表示。

性质5设X和Y为可删除项集，若P(X)⊆P(Y)，则Gain(X∪Y)等于Gain(Y)，X和Y都不是最大可删除项集。

证明由于P(X)⊆P(Y)，所以P(X∪Y)等于P(Y)，根据公式(1)可得Gain(X∪Y)等于Gain(Y)，X∪Y也是可删除项集，由于X和Y都是X∪Y的子集，所以都不可能是最大可删除集，性质成立，证毕。

推论3设X为某个可删除项集，X∩(ik∪ik+1∪…∪i|L1|) = ∅，ik,ik+1,…,i|L1|是L1中最后|L1|-k+1个项目，Y=X∪ik∪ik+1∪…∪i|L1|，若(P(ik)∪P(ik+1)∪…∪P(i|L1|)) ⊆P(X)，且MES中没有长度大于Y的项集，则Y一定为最大可删除项集。

证明假设Y不是最大可删除项集，最大可删除项集Z是Y的超集，则Z中包含的项目个数必然多于Y中包含的项目个数，与推论中的条件相矛盾，推论成立。

证明根据可删除项集的定义和性质1可知，X∪ik不是可删除项集，则其超集一定不是可删除项集。

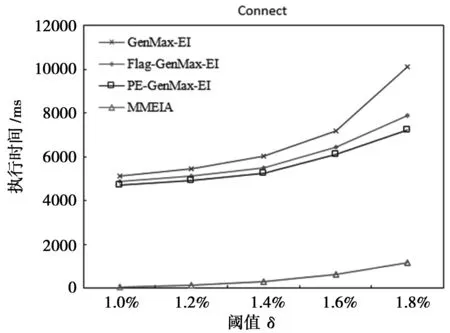
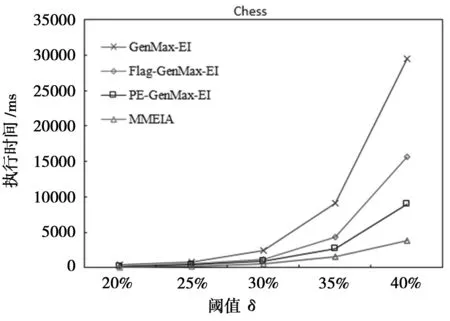
根据上述产品集的包含关系和相关性质，MMEIA算法采用的挖掘策略如下：(1)扫描一遍PDB，计算出满足阈值δ要求的所有可删除项目和对应的产品集，按照产品集由大到小的顺序将项目放入L1[i].items中，将项目对应的产品集放入L1[i].P中；(2)按照深度优先的搜索方式，对L1中的项目进行合并，搜索以L1[i].items为前缀的最大可删除项集，如果L1[i].items∪L1[j].items(i

2.2 剪枝策略

在挖掘最大可删除项集的过程中，根据性质6，如果L1[i].items∪L1[j].items的收益值不满足阈值要求，则不用再搜索以L1[i].items∪L1[j].items为前缀的所有项集，减少了最大可删除项集的搜索空间。根据推论3，如果L1中第k、k+1、…、|L1|个项目对应的产品集都包含在某个项集对应的产品集中，则不用再搜索以ik、ik+1、…、i|L1|为前缀的最大可删除项集，减少了候选项集的数量。

根据性质4和性质5，在对项集进行合并时，如果有多个可删除项集对应的产品集都包含在某个可删除项目集A对应的产品集中，则可以直接将这些项集合并到一起，并将A的收益和产品集作为合并后的项集的收益和产品集，不用再重新计算收益值，减少了候选项集的数量和计算候选项集收益所花费的时间。

例如，如果X∈C(Z)，Y∈C(Z)，Z是可删除项集，则P(XYZ)=P(X)∪P(Y)∪P(Z)=P(Z)，因此可以得到Gain(Z)=Gain(XYZ)，所以XYZ也是可删除项集，其收益值可由Z的收益值直接得到，不需要再进行计算，其子集XY、XZ、YZ等不需再产生和计算收益，可以直接从搜索空间中删除。

2.3 算法描述

根据上面的算法思想和剪枝策略，将MMEIA算法描述如下：

输入：PDB、阈值δ、MES={ }

输出：MES

(1)扫描PDB，找出满足δ的所有可删除项目放入L1[i].item中，相应的产品集放入L1[i].P中;

(2)按照每个L1[i].P中产品集大小的降序对L1进行排序;

(3)fori←1to|L1| -1do{

(4)X=L1[i];

(5)if(FindMaxEI(X,L1,i+1) =1)break;//X之后的所有项目都已合并，挖掘结束

(6) }

(7) 输出MES

FindMaxEI过程如下：

(1)ProcedureFindMaxEI(X,L1,position) {

(2)temp= 0,supersetFlag= 0;//若X的超集是最大可删除项集，则supersetFlag为1

(3)forj←positionto|L1|do{

(4)if(X.P⊇L1[j].P) {

(5)X.items=X.items∪L1[j].items;

(6)if(j=|L1| ) {

(7)if(|L1| -X在L1中的位置+1 =X中包含的项目数){

(8)MES=MES∪X;return1;}//X之后的所有项目都已合并，挖掘结束

(9)elseif(X⊇{ik,ik+1,…,i|L1||k∈[1,|L1|]}) {

(10)MES=MES∪X;return3;}//结束以X为前缀的最大可删除项集挖掘

(11)else{MES=MES∪X;return2;}

(12) }

(13) }

(14)else{

(15)Y.items=X.items∪L1[j].items;

(16)Y.val=X.val+ ∑PiL1[j].P∧PiX.PPi.val;

(17)if(Y.val≤Sum(PDB)×δ) {

(18)Y.P=X.P∪L1[j].P;

(19)if(j<|L1| ) {

(20)temp=FindMaxEI(Y,L1,i+1);

(21)if(temp= 1){return1;}//Y之后的所有项目都已合并，挖掘结束

(22)elseif(temp=2) {supersetFlag= 1;}//X的超集是最大可删除项集

(23)elseif(temp= 3) {return3;} }//结束以X为前缀的最大可删除项集挖掘

(24)elseif(j=|L1|andsupersetFlag= 0) {

(25)if(|L1| -Y在L1中的起始位置+1 =Y中包含的项目数){

(26)MES=MES∪Y;return1;}//Y之后的所有项目都已合并，挖掘结束

(27)elseif(Y⊇{ik,ik+1,…,i|L1||k∈[1,|L1|]}) {

(28)MES=MES∪Y;return3;}

(29)else{MES=MES∪Y;return2;} }

(30) }

(31)elseif(j=|L1|andsupersetFlag= 0){MES=MES∪X;}

(32) }

(33) }//endfor

(34) }//endprocedure

2.4 算法示例

为了说明算法的执行过程，将MMEIA算法用于表1的产品数据库，在δ=15%(阈值为885)时其挖掘最大可删除项集的过程如图1所示。算法首先执行第(1)(2)行，找出可删除项目的集合L1={i5,i6,i4,i8,i7}，并按照每个项目的产品集由大到小排序，每个项目的产品集和收益值都已在图1中列出。算法从第(3)行开始挖掘最大可删除项集，在第(5)行调用FindMaxEI过程，先挖掘以i5为前缀的所有最大可删除项集。在FindMaxEI过程中，先判断i5的产品集P(i5)是否包含i6的产品集P(i6) (执行第(4)行)，因P(i5)不包含P(i6)，执行流程跳转到第(14)行，合并i5和i6，计算Gain(i5∪i6)，由于Gain(i5∪i6) =1 300，大于阈值885，所以{i5,i6}不是最大可删除项集，执行流程再跳转到第(31)行。由于此时的j不等于|L1|，本次循环结束，执行流程转入下一次循环，求解i5∪i4。由于Gain(i5∪i4) 和Gain(i5∪i8)都大于阈值，所以{i5,i4}和{i5,i8}都不是最大可删除项集。在计算i5∪i7时，因P(i5)不包含P(i7)，执行流程跳转到第(14)行，计算Gain(i5∪i7)=850，小于阈值，又因i7是L1中最后一个项目，此时j等于|L1|，执行流程跳转到第(24)行。由于{i5,i7}包含L1中最后一个剩余项目i7，第(27)行的条件满足，将{i5,i7}放入MES中，结束以i5为前缀的挖掘过程并从FindMaxEI过程中返回。

图1 MMEIA算法在表1中的挖掘结果(δ=15%)

算法再挖掘以i6为前缀的所有最大可删除项集，在调用FindMaxEI过程以后，由于P(i6)包含P(i4)，执行第(5)行，合并i6和i4。又由于P(i6)也包含P(i8)和P(i7)，所以算法连续将i8和i7将与i6合并，在合并i7以后，此时j=5，等于|L1|，i6在L1中的位置是2，合并后的项集{i6,i4,i8,i7}中包含有4个项目，所以第(7)行的条件满足，将{i6,i4,i8,i7}放入MES中。由于i6以后的所有项目都已合并，所以算法终止，挖掘得到两个最大可删除项集{i5,i7}和{i6,i4,i8,i7}。

3 实验验证和分析

3.1 实验验证

为了验证算法的性能，在Window10系统、酷睿i5四代处理器、内存8GB的台式机上用C++语言实现了MMEIA算法和文献[8]中的GenMax-EI、Flag-GenMax-EI和PE-GenMax-EI算法，并采用了与文献[8]相同的实验数据集，如表3所示。在实验中分别运行本文算法和对比算法，记录它们的运行时间，如图2、图3和图4所示。通过算法的实验对比结果可以看出，MMEIA算法在挖掘最大可删除项集时的效率要高于GenMax-EI、Flag-GenMax-EI和PE-GenMax-EI算法。

图2 Mushroom数据集测试

图3 Connect数据集测试

图4 Chess数据集测试结果

表3 实验数据集

3.2 结果分析

MMEIA算法充分利用了产品集之间的包含关系，结合深度优先搜索过程中的剪枝策略，在挖掘过程中减少了候选项集的产生数量和计算候选项集收益的花费，从而节省了存储空间和时间开销。算法通过一次扫描产品数据库，计算出可删除项目和相关信息，后续挖掘过程中，不需要再扫描产品数据库，因而节约了算法的执行时间。根据产品集之间的包含关系，算法在最好情况下的时间复杂度可以达到○(n)(n为可删除项目的个数，即|L1|)，最坏情况下的时间复杂度可达到○(n2)。由于算法中设置了supersetFlag标记，当某个可删除项集X的超集是最大可删除集且已搜索到L1中最后一个项目时，则可以直接返回到递归的第一层，进一步减少了候选项集产生的数量和计算项集收益的时间，从而提高了算法的效率。在PE-GenMax-EI算法中，由于采用了按层搜索的策略，挖掘过程中会产生大量的候选项集，而计算候选项集的收益要花费大量的时间，因此相对MMEIA算法来说，PE-GenMax-EI算法的整体性能相对较低。

4 结 语

本文提出的挖掘最大可删除项集的MMEIA算法，利用了项目集对应产品集之间的包含关系和可删除项集的相关性质，大量的减少了候选项集的数量，节省计算候选项集收益所需的花费，根据实验结果和性能分析可以看出，该算法能够有效解决最大可删除项集挖掘问题。