高中数学结构不良问题的教学策略*

曹茂宏 从 品 刘其群 曹思齐 (江苏省南京市金陵中学 210005)

2016年，教育部考试中心提出构建高考评价体系，高考数学科研究了基于高考评价体系的数学科考试内容改革实施路径[1]，而在新高考的数学考试中引入、设置结构不良试题就是其路径之一．随着新高考的推行，结构不良试题的命制成为研究热潮，但有关教学中结构不良试题如何进行组织及实施的研究较少，而这又是亟需解决的．

1 结构不良问题的内涵

问题的核心要素包括：初始状态、目标状态及算子[2]．初始状态是指所需解决问题的信息；目标状态是指问题所要得到的结论；算子是指问题解决中使用的方法和途径．结构良好问题(well-structured problem)是此三者都很明确的问题，而结构不良问题(ill-structured problem)是三者中至少有一个没有明确界定的问题．

结构不良问题并不是问题本身有错误或者不恰当，而是它没有明确的结构或解决途径．结合数学科和高考的特点，数学科的结构不良问题主要具有如下特征：(1)问题条件或数据部分缺失或冗余；(2)问题目标界定不明确；(3)具有多种解决方法、途径；(4)具有多种评讲解决方法的标准；(5)所涉及的概念、规则和原理等不确定[3]．

结构不良问题的解决过程能有效激发学生的求知欲，帮助学生多角度把握问题本质，培养学生的数学建模能力，引导学生追求知识背后的价值，形成跨学科综合解决问题的关键能力．因此，基于结构不良问题的解决实施教学具有深远意义．

2 结构不良问题促进高中数学的学习

在结构不良问题中，初始状态、目标状态及算子，至少其中之一不明确，这需要在解决问题的过程中联系实际进行类比、抽象、建模，一些数据还需学生自己去测量，这些体验过程将极大丰富学生的数学学习经历．

从学科知识的角度看，结构不良问题是有思维空间和挑战性的学习任务的，结构不良问题的解决需要经过类比、综合运用所学知识．所以解决结构不良问题会让学生认识到知识背后的逻辑、意义和价值，帮助学生深入把握知识的产生与来源、事物的本质与规律、知识的关系与结构、知识的意义与价值．

从学科思维的角度看，结构良好问题往往与学生已经解决过的问题相同或相似，学生只需调用早已知道的解决路径就可以解决问题．而结构不良问题往往没有明确的解题路径，需要学生大胆猜想、大胆推测，发现和创造新的问题解决方案.这种创造性的学习调动了学生的积极性，帮助学生深入思考，提升学生的问题解决能力，发展分析、评价、批判等高阶思维能力，从而让学生深刻把握学科思想与方法．

从学科价值的角度看，数学是注重定量与确定性，讲究严密逻辑的一门学科，而结构不良问题具有条件模糊、解决方案多样、结果开放等特点，与数学学科本身特点产生强烈的认知冲突．能解决真实生活中的复杂问题是深入学习的根本价值，也是落实数学学科核心素养的重要标志．所以基于结构不良问题的解决来开展教学，能有效提升学生的批判性思维和解决复杂问题的能力．

3 结构不良问题解决的教学策略

以往的教学中，学生接触的试题一般都是结构良好的，而随着新高考的推行，结构不良试题已经成为必考题．在结构不良试题缺乏的情况下，教师如何组织结构不良问题，即对结构不良问题如何开展教学，是当下需要研究的问题．在学科考试中，受到时间和空间的限制，试题不能太难、答案不能太开放，所以考试中的结构不良问题具有一定的局限性和模式化．但实际教学中，结构不良问题可以加大开放性，这更有助于培养学生发现和提出问题的能力，以及应对现实挑战的创新能力和实践能力．

笔者认为，在教学中结构不良问题的设计可以从教材、原有结构良好问题及实际生活情境中组织情境和问题，以体验式、案例式及项目式教学为主，提升学生多维度思考空间，更好地拓展学生的思维创新能力，促进学生的合作能力发展．

3.1 甄别教材中的问题，开展体验式教学

苏教版高中数学教材中存在大量的结构不良问题．这需要教师平时教学时留心注意，把结构不良的问题甄别出来并有效组织教学，通过让学生亲身体验、观察反思不定期地形成概念，获得相应知识．

案例1苏教版高中数学教材必修5“数列”中的例题：某种卷筒卫生纸绕在盘上，空盘时盘芯直径40 mm，满盘时直径120 mm．已知卫生纸的厚度为0.1 mm，问：满盘时卫生纸的总长度是多少米？

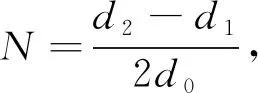
体验式教学是一个体验、反思、概括与应用的过程，使学生以亲身体验的方式加入学习过程，融入自我体验，有助于学生加深对所学知识的理解．学生通过这一亲身体验过程，巩固了有关等差数列、等差数列的公差及等差数列前n项求和的书本知识，同时体验了数学中建立模型、求解模型、检验模型的基本过程，真正做到“做中学”，提升解决实际问题的能力．教材中一些素材和问题可以让学生亲身体验，从而对所学知识获得更深层的理解．

3.2 改编结构良好问题，开展案例式教学

很多结构良好的问题在学习知识后作为巩固所学知识提供给学生训练，教师可以将结构良好的问题转化为结构不良问题，在学习知识前提供给学生解决，此时将结构不良问题作为知识学习的载体和典型案例，学生在解决案例的过程中学习新知识，掌握学科思想与方法，将结构不良问题作为打开核心概念学习的钥匙．

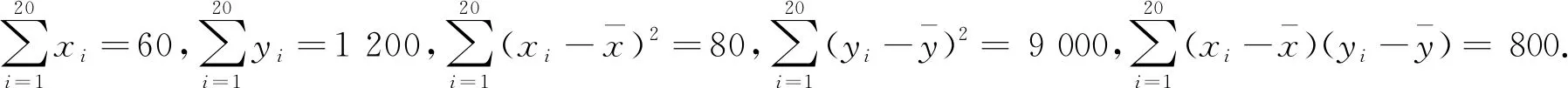
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数)；

(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01)；

(3)根据现有统计资料，各地块间植物覆盖面积差异很大．为提高样本的代表性以获得对该地区这种野生动物数量更准确的估计，请给出一种你认为更合理的抽样方法，并说明理由．

上题是结构良好的题目，主要考查回归方程相关知识，在学习回归方程时可以将这一结构良好的题目改编为结构不良问题：

人口是当今世界各国普遍关注的问题．认识人口数量的变化规律，可以为有效控制人口提供依据．下表是1964—2009年我国人口数据资料：

年份1964196919741979198419891994199920042009人数/万70 49980 67190 85997 542104 357112 704119 850125 786129 988133 450

试估计我国2021年的人口数．

该题是初始状态明确、目标状态和算子不明确的结构不良问题．把该案例放在学习回归分析之前，能够让学生多角度思考问题，有利于促进学生的发散性思维和创造性思维．实际操作中，教师可以加入问题串：(1)请作出时间—人口的散点图，能不能根据图象估计2021年的人口数？(2)根据图象，你准备选择哪种函数拟合数据？(3)早在1789年，英国T.R.Malthus提出自然状态下的人口增长模型y=y0erx，其中x表示经过的时间，y0表示x=0时的人口，r表示人口的平均增长率．这个模型会不会比你的模型好？上述问题串更利于课堂的把控．

通过上面的问题分析，学生初步建立数据统计知识，理论探究线性拟合、指数拟合知识，实际操作数据回归分析．学生根据离散图象，不会选择线性拟合，而可能会选择指数拟合或二次拟合，那么对于自己选择的模型与Malthus人口模型孰优孰劣，学生自然会想到选择一个量来刻画拟合程度，这正是回归分析需要解决的问题．这就实现了依靠这一个案例“点”的学习，带动整个回归分析“面”的学习．

案例式教学是按照案例的方式就一个对象进行专题式教学，体现为主体性、可操作性和综合性强，给学生更为广阔的探索空间和创新空间．这里需要学生从模糊的问题情境中发现和提出问题，需要多角度思考，对学生的创造性思维提出了更高的要求．上述分析过程正是结构不良问题所缺失的，但却是深入学习的必要条件．学生在解决该案例的过程中，不仅学习到数据拟合和回归分析的相关知识，还体验到转化与化归的数学思想，提升了数学建模、数据分析的核心素养．

3.3 模拟实际生活情境，开展项目式教学

现实生活中存在大量的结构不良问题，很多实际问题由于空间、时间和成本巨大，无法在课堂和学生有限的时间、空间内完成，教师可以模拟相似的情境，让学生去解决．为了模拟得更加真实，可以采取项目式教学方式，以此来培养学生的综合思维、知识迁移能力和跨学科解决情境问题的能力．

案例3在建设城市隧道时，往往需要勘测山体一端A到另一端B的距离，如何利用高中所学知识来测量该距离呢？

在实际教学中，由于空间的限制，无法将学生带到山前进行测量，但可以做一些示意图来模拟上述情境．让学生分组进行项目式学习．项目要求：在实际测量中，操作简单易行，通过测量的基本量准确计算出AB的距离．学生在此项目式学习中，需要绘制示意图，标出需要测量的基本量，给出AB的计算公式．

求距离两点间不可通过又不可视两点间可视但不可达两点都不可达

总之，项目式教学是将学生置于解决问题的真实情境中，灵活运用知识，发展高层次思维能力，让其成为自主的学习者和有效的合作者．在复杂、真实的实际问题中，学生往往不明确哪些概念、规则、原理对解决问题有用，需要从诸多现象中分析、确定解决方案，把所学的学科知识和技能迁移到真实的生活情境中，同时在真实情境中通过体验、探究来建构自己的知识，逐步提升可迁移能力、高级思维能力及数学建模等核心素养．

4 结语

结构不良问题是新课程、新高考的一个亮点，可有效激发学生的求知欲，帮助学生多角度思考问题，有利于学生发现并提出问题、分析并解决问题能力的培养以及学科核心素养的形成．在教学中，教师可以甄别教材中的问题，开展体验式教学；改编结构良好问题，开展案例式教学；模拟实际生活情境，开展项目式教学．根据结构不良问题的特性，一方面课堂的开放性可以设置得更高，更加具有情境化和生活化，为教学提供了更广阔的空间，更利于学生的能力培养；另一方面因为教学时间和空间的限制，教学设问要指向课堂教学目

标，做到问题开放有度、解决有法，启发性和思考性相得益彰，这对教师的能力提出了更高的要求．