基于科学思维提升的实验教学设计——以“随盘转动物块的向心力”教学为例

吴 君 郭月斌

（龙海第一中学，福建 漳州 363100）

一、“转盘—物块”模型的思考

高中物理中，静摩擦力具有多变性和抽象性。水平圆周运动中的“转盘—物块”模型，是高中物理向心力的内容，常以习题形式出现，其考点主要涉及物块的受力分析和系统的临界问题等。理论的教学方式，对初步形成抽象理论的高一学生而言，易造成理解性偏差。对随盘转动物块用轻绳连接后，摩擦力方向变化和绳子拉力出现变化的临界条件，学生一般表现为不分过程，不加选择的套用公式，无法达到科学思维能力的有效培养。

科学思维是基于事实证据和科学推理，对不同观点和结论提出质疑和批判，进行检验和修正，进而提出创造性见解的能力与品格。［1］物理模型是物理试题设计的基础，解决物理问题需要抓住模型临界状态的特点。新课标、新高考对建模、实际应用等能力，有更明确的要求。在物理教学中，可设计必要的实验实际情境，结合学生的思维层次，切实提高学生对模型的识别能力、迁移能力和应用能力。［2］让学生不断突破自我潜意识带来的错误认知，理解多种模式归一的模型核心特点。

限于中学物理知识体系及学生的思维能力，笔者通过自制教具，基于经验事实，建构物理模型，让学生对模型的认识是由实际问题引发，再迁移到抽象思维逐步加工加深，调动学生逻辑推理的积极性，在模型建构中进行过程性分析，概括模型内在规律，从而达到深度学习下的思维进阶。

二、基于科学思维提升的模型建构过程

（一）科学思维启动——单物随盘转

创设情境：以学生亲身体验游乐场转盘的视频引入（图1），分析（1）随盘转动的人，在转速达到一定程度时，会滑出的原因。（2）此过程物体所受摩擦力f 大小怎么变化？

图1

引导学生归纳：物体随盘做匀速圆周运动时，所受静摩擦力提供向心力，方向指向圆心，初步构建“转盘—物块”模型。

目前，中学教学仪器无法对转盘上动态的静摩擦力进行直接展现及测量。如何让学生感知静摩擦力的变化，帮助学生建立证据意识以解决模型难点，笔者用减速电机，调压电源，木板，毛巾，组装成能缓慢调速，直径50cm 的水平转盘。搭配微型无线摄像头（自带电脑监控软件），用于转盘上不易观察现象的跟踪拍摄。

图2

实验情境：放上刷毛的物块随盘转动，让学生直接观察，刷毛的形变程度（图3），用毛刷把静摩擦力的大小和方向粗略地显示出来的方法，证实学生想法。再由学生分析出小物块即将发生滑动时角速度的临界值。

图3

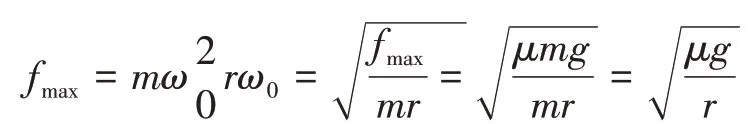
在此提问学生，ω=时，向心力分别为多少？学生思考后，能准确回答。

［设计意图］通过刷毛形变程度，直观、便捷地展示沿半径方向静摩擦力的变化情况，学生使用直接证据，定性评估向心力的变化。此过程也让学生将实际问题中的对象和过程转化成物理模型。

（二）科学思维发展——牵物随盘转

1.初始无拉力的牵连

问题情境：连接物块和转轴的轻绳刚好被拉直（图4）设问：当物体随盘转动，角速度较小时，向心力由什么力提供呢？绳子拉力还是摩擦力？

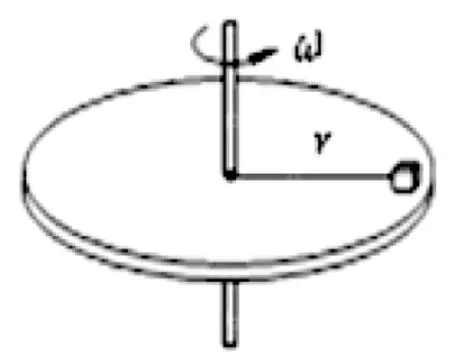
图4

学生受绳子干扰，很多会以为随盘转动的物体马上受到拉力。笔者采用DIS 实验系统中的无线力传感器，其精确度达到0.01N，采集频率达到50Hz，将其作为转盘上的物块。在配套软件中，笔者设置纵轴为拉力大小，横轴为时间（对应不同的大小角速度的时刻），实时监测数据，在黑板屏幕上呈现，结合变化规律，引导学生探究绳上力的变化。首先确定绳子处于伸直不紧绷，即示数为零的初状态。缓慢调节转速，力传感器随盘转动（图5），得到拉力的数据图像（图6）。

图5

图6

实验情境1：手控缓慢调速，物体随盘转动稳定较小角速度时（圈1），传感器的拉力值未发生变化；角速度达到一定值，拉力才出现（圈2）；角速度较大并稳定时，拉力值稳定（圈3）（基于高中知识特点及学生能力，此处不对曲线趋势进行解释，只强调拉力的出现，物体做匀速圆周运动的角速度要达到临界值）。

学生能根据拉力的实验数据规律，分析出：起始阶段，完全由静摩擦力提供物体的向心力，达到最大静摩擦后，绳子拉力才出现，其临界向心力表达式如下：fmax=>ω0时fmax+T=mω2r

2.初始有拉力牵连

问题情境：（图6）实验末尾现象（圈4），绳子拉力数据未回到0N，这是为何？

让学生展开讨论，积极思考，并通过启发式反问，让学生思维逐步完善。物体牵扯弹簧拉伸一定长度后，放到桌面会有什么现象？绳子的微小形变肉眼看不到，但可分析出此时绳子处于绷紧状态，静止时，物体所受拉力与静摩擦力等大反向。在此，顺势引入下个学习环节。

设计问题串：①若以上个实验结果为起始状态，即轻绳（轻弹簧）有初始拉力T0=f0，物体随盘转动，角速度较小时，请写出物体向心力表达式？学生：T-f=mω2r②根据初始状态T0=f0，分析物体开始随盘做匀速圆周运动时的向心力，是因为物体所受的静摩擦力减小？还是拉力增大？还是两个力一起变化？让学生结合上个实验，再次进行思维碰撞的小组讨论，在同伴互助中学习，展示各小组讨论结果及理由，但不予以评判，直接让学生根据实验现象进行修正。

实验情境2：从上次实验的末状态切入，再次缓慢增加转盘角速度，得到拉力的数据图像（图7）。

图7

学生分析可得：物体做匀速圆周运动，有较小角速度时，拉力仍没有马上改变（圈1），说明先变的是摩擦力，即ω<ω1时T0-f=mω2r；角速度缓慢增加到某个数值，拉力才增大（圈2）；稳定加速度，拉力大小也稳定（圈3）；最后角速度缓慢减小到零，拉力大小（圈4）与起始数据一致。

设问：③拉力变化之前，静摩擦力经历了怎样的变化？学生：先减小到零。④静摩擦力减小到零后，拉力就增加么？学生普遍对此处静摩擦力会反向增大的问题表示难以理解。

实验情境3：本次改用弹簧连接加刷毛的木块，以解决细绳连接无法引起刷毛上下错层形变的效果，并采取划线定位的方式（图8），通过摄像头清楚记录并投影刷毛移动的全过程。

图8

学生直观感知，圆盘转动的角速度缓慢增大的过程中，刷毛由原来水平向左变为竖直再变为向右（图9），即沿半径方向的静摩擦力先减小到零后反向增加了，分析出ω1是静摩擦力反向的临界角速度，即ω=ω1时T0=mω2r。

图9

为此，启发学生思考：因刷毛柔软形变，而通过划线定位可知，下方接触面相对转盘位置不变。如果换成固体物块，弹簧形变量则不会变化，拉力大小就不会改变。至此，学生思维清晰，能自主总结此过程向心力的临界情况：ω1<ω<ω2时T0+f反=mω2r；ω=ω2时拉力改变的临界条件；ω2<ω时T+f反m=mω2r。

学生综合上述实验现象和结论，可以对“转盘—物块”模型进行化繁为简的归纳：1.物块对转盘恰好不发生相对滑动的临界条件：物体受到向心方向的最大静摩擦。2.此类模型，当角速度缓慢增加，先发生变化的力，是还未达到最大值的静摩擦力。

［设计意图］通过数字化多媒体配合教学，让教师精心设计实验环节不会因实验现象的难以观察而草草了事，三组实验现象给学生带来强烈的认知冲突。学生能对随盘转动的物体所受静摩擦力问题的持不同观点，基于事实证据，对结论提出质疑，分析综合信息，进行修正，并解释变化原因，从而理解现象本质，将实际问题抽象简化为模型，进而得出正确性见解，找出规律，形成科学思维，有效完成此过程中，组成向心力的各个力的分析，有利于学生进一步理解第三种拓展情形。

（三）科学思维进阶——连接体随盘转

问题情境：相同的物块A、B，转动半径rA=2rB，连接A、B 物块的轻绳恰好伸直（图10）。思考：①细线上何时出现拉力，出现时A、B 的向心力表达式？②两物块何时开始相对转盘滑动？临界状态的向心力表达式？

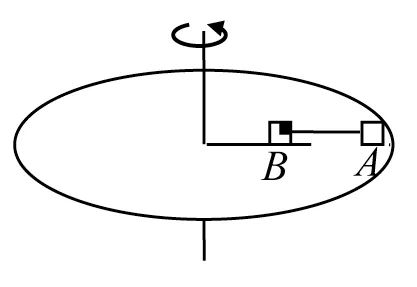
图10

学生根据前面的分析思路，可以自行得出以下过程ω<ω1时，fB=mω2r，fA=mω22r

ω=ω1时，fB=拉力出现的临界条件

ω1<ω<ω2时，fB-T=mω2r，fAm+T=mω22r

追问：外围物体达到最大静摩擦会拉动绳子，此时物体一起滑动了吗？学生不确定实验情境：演示传感器连接体随盘转（图11）：

图11

学生分析得：转动半径大的物块A，先达到最大静摩擦力后，拉力开始增大，整体未滑动（图13）。再增大角速度，直到转动半径小的物块B 也达到指向圆心的最大静摩擦，整个系统才会滑动，相当于系统达到最大静摩擦（图14）。

图12

图13

图14

ω=ω2时，fBm-T=相对滑动的临界条件

ω2<ω时，整体相对圆盘滑动

［设计意图］通过传感器对接测连接体内力变化，同步测量数据和实验画面，给予恰当的思维难度，让学生通过科学推理和科学论证，把实验情境转化为物理模型规律的表述，进而提出创造性见解，提升科学思维。

（四）科学思维有机整合

基于上述模型建立的过程，再引导学生进行相关类型的分析练习（图15），让学生经历“比较—概括—整合”的过程，促进学生研究实际相近问题，学会变通，理解并巩固模型规律的适用条件，从多个视角审视检验结论，发展科学思维。

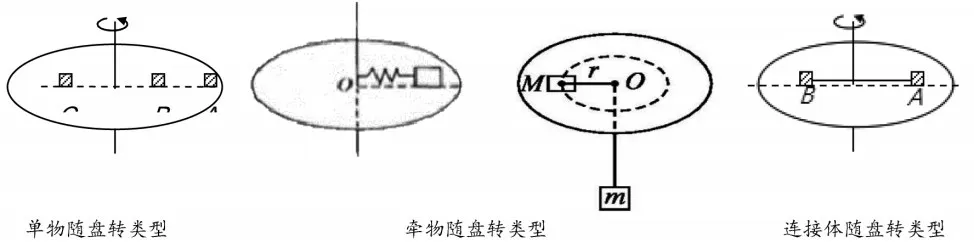
图15

三、结语

通过自制教学仪器，进行半定性、半定量的实验，能无缝对接学生对情境理解的思维障碍，学生从情境中发现和提炼问题，获取客观真实的数据，分析修正自己的假设，运用逻辑和现有知识进行科学论证和解释，重在启发学生形成模型的本质认识和相关规律，帮助学生克服思维障碍，有效落实了物理学科核心素养的培养。课后回访和作业完成的情况表明，学生对物体随盘转动的问题，能进行科学思考。