电场传感器性能改善算法研究

韩 文，吴 健，程珍珍，唐露甜，孙利利，章 凯，张 勇

（1.国网陕西省电力公司电力科学研究院，陕西 西安710199; 2.西安交通大学，陕西 西安710049）

0 引 言

随着电力系统的高速发展，高压（特高压）输电线路日益增多，因静电效应、磁场效应及电晕现象引起的一系列“环境影响问题”对公众生产生活的影响日益突出[1-2]。现实中，输电线路电磁环境会随着电压、电流以及天气原因等众多因素的影响而产生变化，需要进行长期观测统计其规律[3-5]。获取我国输变电工程电磁环境的基本参数，掌握其规律，对指导今后的输变电线路设计和建设具有重要意义；电磁环境监测数据将为我国建设以特高压为骨干网架的坚强智能、绿色、环保电网提供有力的技术支持。针对工频电场，目前主要采用传统的电学式电场传感器[6-9]和光学式电场传感器[10-12]进行检测，能用于实际环境中的电场传感器产品大多来自于国外，国内产品尚处于实验研制阶段，在现场环境下检测误差较大，抗干扰能力差，难以满足实际中的工程需要。

传统的电场传感器存在机械结构复杂、量程窄、温漂大等缺点。为了改善传感器的检测性能，一部分学者[12-14]试图通过改变传感器的结构来改善其性能，如凌碧云等[8]提出了一种谐振式的三维电场传感器，测量范围为0～120 kV，但其交叉灵敏度和测量误差相对较高，分别为5.48%和6.16%，且谐振式的电场传感器谐振频率不易控制。一旦传感器的结构确定，该方法耗费时间和资金成本较大。因此，另外一些方法则是从算法的角度出发，利用机器学习算法改进传感器的性能。李冰等[13]提出了一种基于遗传算法的三维电场传感器解耦标定方法，使合成电场的相对误差从4.4%减小到了1.9%，但该方法存在易丢失最优解的缺点。闻小龙等[14]通过求逆矩阵运算的方法获得传感器的耦合灵敏度矩阵，完成了对其设计的三维电场传感器的标定，最大相对误差为10.2%，未能有效地改善传感器的性能，当计算过程中矩阵奇异或接近奇异时，计算复杂耗时且存在计算误差。

为了进一步提升电场传感器的检测性能，提高电场传感器在检测工频电场的准确度，本文采用国产森馥SEM-600低频电磁辐射测量仪对一台标准工频电场发生器中心区域产生的0～20 kV/m三维电场进行了测量，首先使用最小二乘法评价了该传感器的静态特性指标，得出其误差为13.6%，分析认为，影响其指标性能较低的可能原因为交叉灵敏度。利用机器学习的方法，分别采用BP神经网络、径向基神经网络、支持向量机和遗传算法等算法，对检测数据进行对比分析，得到了优化后的三维电场值，并消除了三维电场之间的交叉干扰，传感器准确度得到较大改善。

1 电场信息获取

标准工频电场发生器实物如图1所示，采用圆形平行极板，极板半径为800 mm，间距为1 200 mm，距地高度为1 000 mm，装配12个半径为800 mm、管径为50 mm 的均压环。在95%置信概率下，标准工频电场发生器的扩展不确定度为0.7 %。

图1 标准工频电场发生器实物图

本文采用国产森馥SEM-600低频电磁辐射分析仪对工频标准电场发生器中心区域的工频电场强度进行了测量。以电场发生器的中心为原点建立了三维空间坐标系，轴向为z轴，径向是xoy平面（左手系）。传感探头放置于工频标准电场发生器两极板的正中心，如图2所示。启动标准电场发生器产生标准电场，国产森馥SEM-600三个正交电场传感器在图2中对标准电场产生响应，工频标准电场变化范围为0～20 kV/m。在标准电场发生器产生的工频电场方向不变的前提下，旋转传感探头，分别使三维传感探头处于图2中定义的3种不同姿态，从而分析传感器的交叉敏感系数。 姿态1、2、3分别将传感器的z、x、y轴与电场发生器的z轴平行放置。

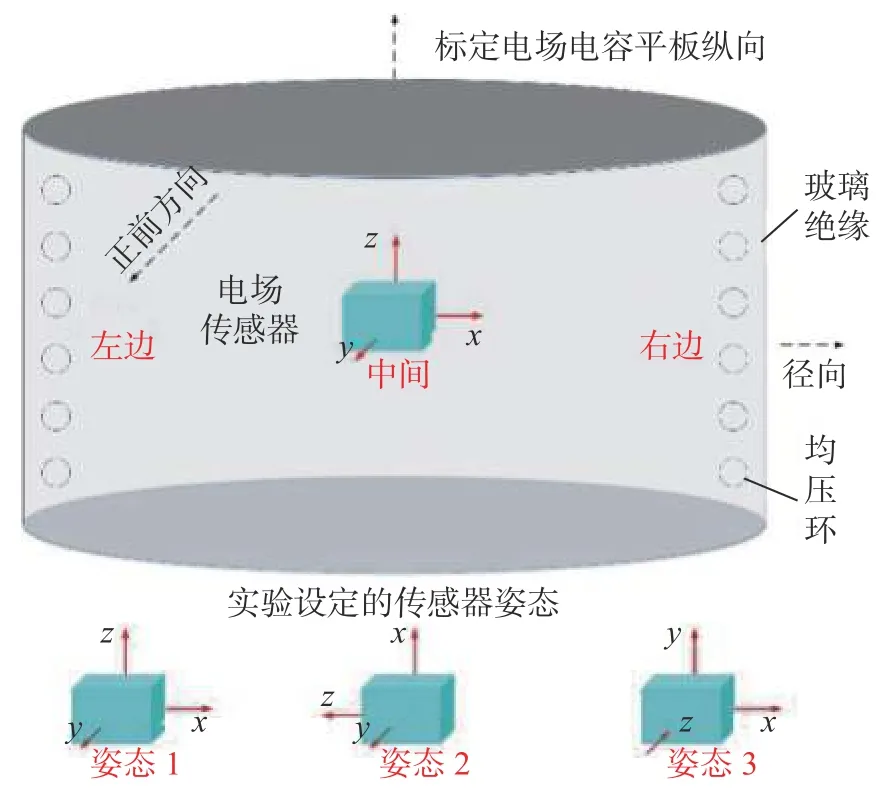
图2 森馥SEM-600电场传感器测量过程示意图

2 三维电场提取

2.1 三维电场分解

将电场矢量E分解为x、y、z 3个互相垂直方向上的电场分量（图3），即

图3 三维电场分解原理图

因此，只要测得电场在空间x、y、z 3个方向上的3个分量，就可得到被测电场强度E：

其中|E|为电场的模值。

2.2 三维工频电场检测结果

本文对Ex、Ey、Ez每个方向进行5组正反行程的实验，共获得了15组三维电场值数据。另外，为了验证算法的效果，还额外进行了3组正反行程的实验。图4（a）～图4（c）分别为传感器z轴向上时对电场发生器产生的工频电场矢量E在x、y、z3个方向上的分量值的响应Ex、Ey、Ez，可以看出，Ez的值最大，与标定电场大小及方向保持一致；电场模值|E|可由公式（2）计算得到。表1为姿态1正行程采集数据。

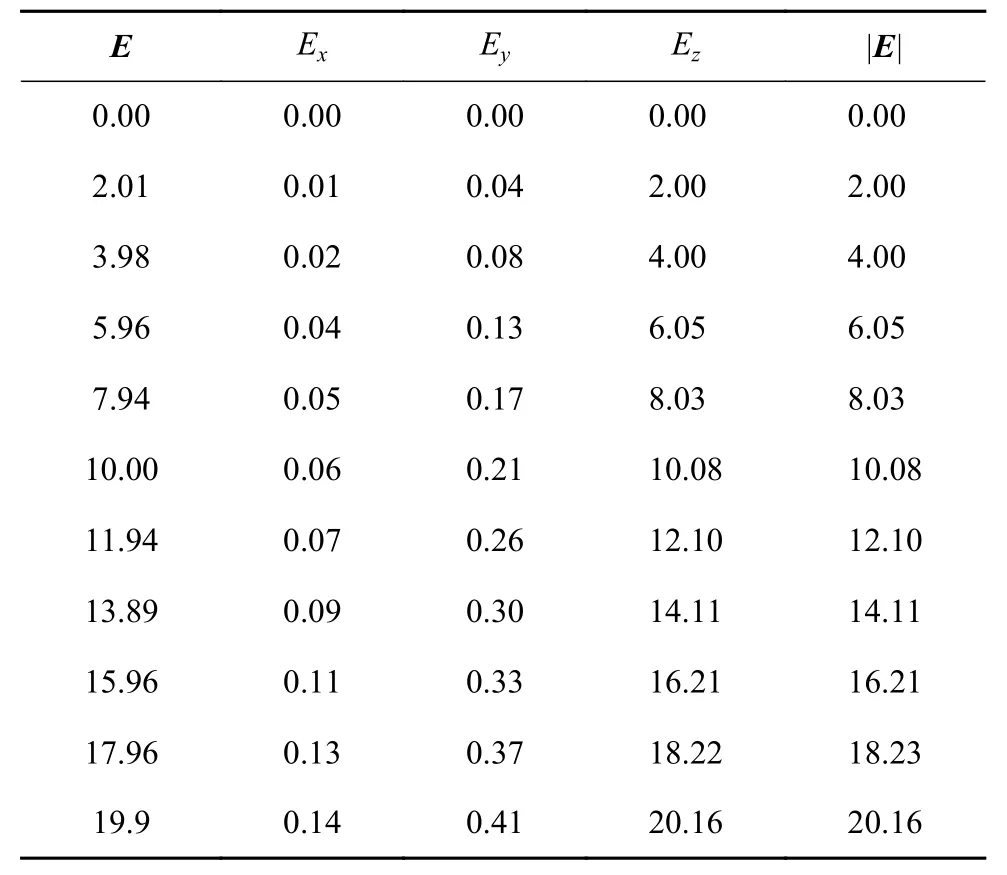
表1 传感器处于姿态1时三维电场检测结果（部分） kV/m

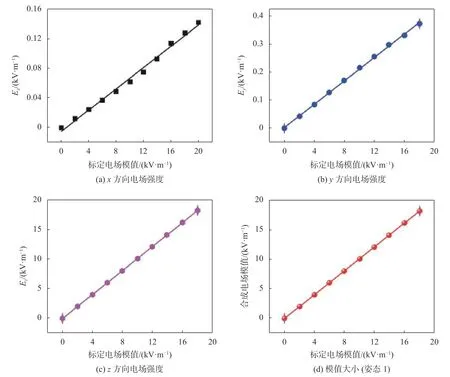
图4 各方向电场强度及模值大小（姿态1）

2.3 传感器静态性能指标计算

为了评价该传感器的性能，依据国家标准GB/T 18459—2001 《传感器主要静态性能指标计算方法》，首先采用了最小二乘法对其准确度指标进行计算，主要包括线性度、迟滞、重复性。

由实验数据进行实验建模，采用下式表示传感器的静态模型，即求取多项式的各项系数：

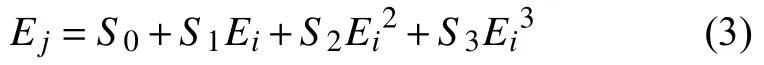
当采取简化的直线方程来表示静态模型时，则只需求取拟合直线的零位与灵敏度两项系数。

设拟合直线方程通式为

则第i个标定点的标定值Ei与拟合直线上相应值的偏差为

最小二乘拟合直线的拟合原则是使N个标定点的均方差为最小值：

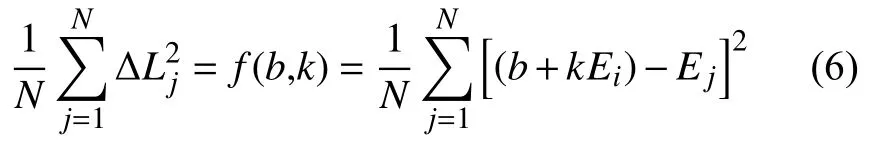
由一阶偏导等于零，即

故最后计算得最小二乘拟合直线方程为

该电场传感器场强测量结果Ej与被测电场模值Ei之间的静态模型。

1）线性度δL

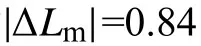
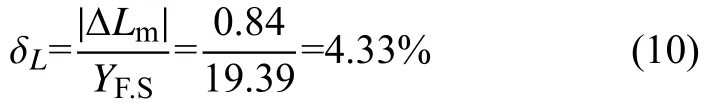
2）计算迟滞δH

先计算各标定点的滞后差=正行程（平均值）-反行程（平均值），选取其中的最大值为|ΔHm|=0.17（kV/m），则有：

3）计算重复性δR

重复性用引用误差形式表示为:

其中ΔR为同一输入量对应多次循环的同向行程输出量的分散程度。计算可得最小二乘的重复性为8.41%。

4）计算误差A

A由线性度ΔL、迟滞ΔH与重复性ΔR的绝对值求和得出：

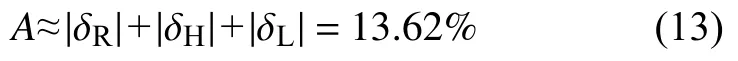
根据拟合直线方程 （5）计算各标定点的拟合值E′d、最大拟合偏差|ΔLm|、最大迟滞偏差|ΔHm|以及重复性偏差ΔR，计算线性度ΔL、迟滞ΔH、重复性ΔR及误差A这4个性能指标，结果见表2。

表2 传感器基本质量指标

可以看出，当采用传统的最小二乘方法计算该电场传感器的静态指标，传感器的准确度较大，很有可能是因为电场三维分量的检测存在交叉干扰，导致传感器性能降低。因此，还需要对传感器的交叉灵敏度做分析。

2.4 电场三维分量的交叉敏感

交叉灵敏度系数αm-n（表3）用于评价非目标参量En对被测目标参量Em的影响程度，计算式如下：

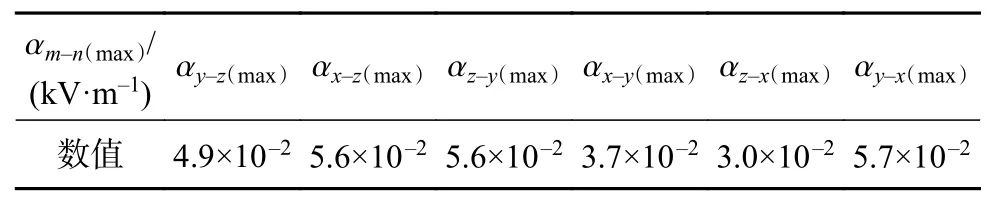
表3 最大交叉敏感系数αm-n（max）

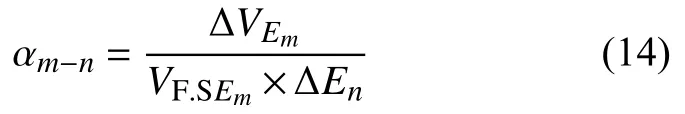
式中：m,n=x,y,z且m≠n；

ΔEn——非目标方向电场变化量；

表3说明三维电场分量之间都存在着交叉干扰，x方向电场分量Ex对分量Ey交叉干扰最大。交叉干扰的存在，无疑会降低传感器检测结果的准确度。因此，建立基于神经网络、支持向量机等智能算法消除交叉干扰，以提高电场传感器的性能。

3 传感器性能分析及改善

正如2.3节的分析，现场测量电场用的森馥SEM-600三维电场间存在着交叉干扰的影响，因此采用机器学习的方法，消除交叉干扰，提高电场传感器的性能。通过对比4种智能算法对性能改善的效果，选出最优方法。

3.1 基于BP神经网络的传感器读数模型建立

研究采用BP神经网络融合方法减小方程（5）的拟合误差。构建3个输入神经元节点、7个隐层神经元节点、4个输出神经元节点的BP神经网络（BPNN）（图4），电场三维分量的检测结果 Ex、Ey、Ez作神经网络的3个输入，电场强度的模值|E|和E′x、E′y、E′z为神经网络的4个输出。

3.1.1 BP神经网络样本文件的建立

在电场发生器的中心位置，三维电场传感器对0～20 kV/m量程（步长为2 kV/m）的工频电场进行了5个正反行程的检测，获得了360组样本数据，即x、y、z 3个方向共有360组样本数据。在电场量程范围内抽取了300组数据作为训练样本，用于建立神经网络读数模型；剩下的60组数据作为检验样本，用于检验神经网络的读数结果是否达到期望的误差要求。

3.1.2 网络结构参数的确定

基于Matlab软件的newff函数建立神经网络训练模型，图5输入层采用purelin纯线性函数，输出等于输入；隐层传递函数采用logsig函数，对输入层的输出加权后进行归一化处理，去除白噪声；输出层采用purelin纯线性函数，将隐层输出量加权求和后输出。当输出层的输出结果误差满足对误差的期望要求时，训练结束。然后，用函数net.IW、net.LW分别获取输入层和隐层间的权值wij，及隐层和输出层间的权值vjk；用net.b分别获取隐层和输出层的阈值bj、ck；从而确定神经网络的结构参数。

图5 神经网络读数模型结构图

①输入层

输入层节点i的输出为：

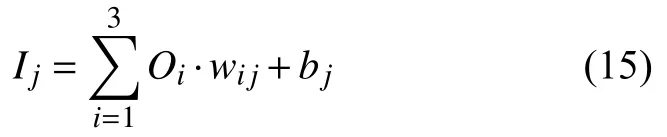
式中：wij——隐层第j个隐层节点与第i个输入节点的连接权值，j=1,2,···,7；

bj——第j个隐层节点的阈值。

节点j的输出为：

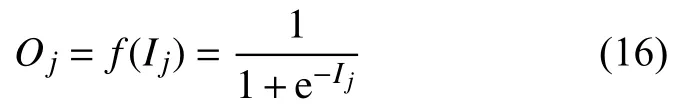
②输出层

第k个节点的总输入为：

式中：ck——第k个输出节点的阈值；

vjk——隐层第j个隐层节点与第k个输出节点的连接权值。

节点k的输出为：

式中：y1——|E|；

y2、y3、y4——E′x、E′y、E′z。

3.1.3 BP神经网络读数模型性能检验

神经网络读数模型能否实用，需要用检验样本验证，检验样本误差达标即验证合格后，获得BP神经网络的结构参数wij、vjk、bj、ck（表4）。

将检验样本数据和表4数据代入式（15）～（18）后，得到被测电场Ei的检验结果E′i。基于最小二乘法拟合获得两个参量的关系式：

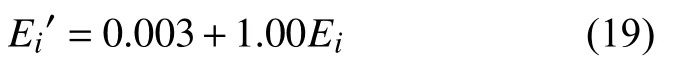
表4 BP神经网络权值、阈值表

根据式（10）～（13）计算了线性度、迟滞、重复性和误差（表5）。表2与表5数据的对比说明，经BP神经网络融合后，传感器的指标（线性度、重复性、迟滞和误差）较基于最小二乘法融合后的传感器指标都有一定程度的改善。相对于最小二乘法而言，BP神经网络是基于误差逆向传播的算法，理论上通过不断迭代，可以实现误差的最小，这也是经BP神经网络融合后，传感器性能指标提高的原因。

表5 基于BP神经网络模型的传感器性能指标

3.2 基于支持向量机的传感器读数模型

从3.1节中可以看到，经过BP神经网络建模后，传感器的相关指标有了一定提升，但是效果并不明显。BP神经网络建立的读数模型的性能取决于标定数据的数量，数量越多，融合结果误差越小；而在实际应用过程中所获得的标定数据（样本）数量往往是有限的，导致误差增大。为解决有限样本的训练问题，这里采用小样本学习机理的支持向量机技术建立传感器的读数模型。

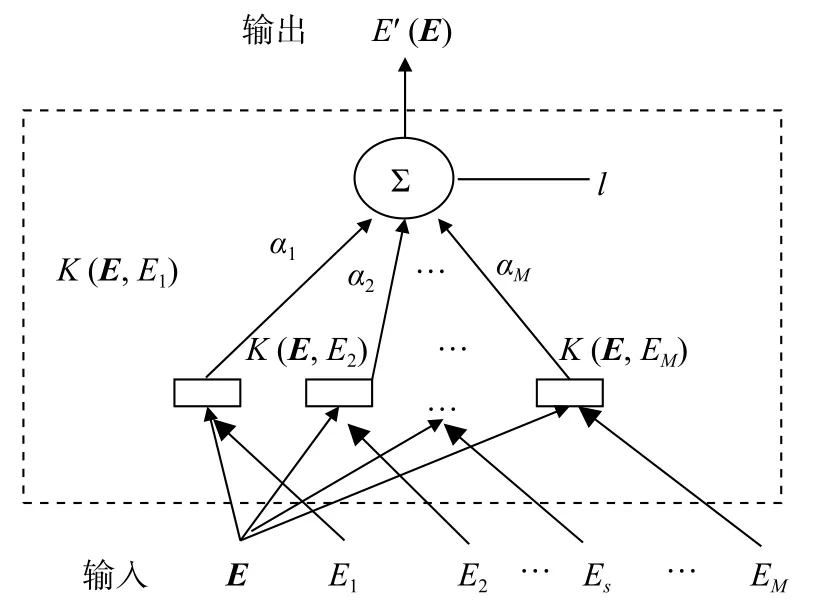
图6 支持向量机模型

这里采用径向基核函数：

其中g为核函数参数，且g＞0。

径向基核函数作为支持向量机的核函数，只需调节惩罚因子C和核函数参数g两个相关参数，就能得到理想的分类准确率。

采用粒子群优化，经迭代计算得惩罚因子C和核函数g的最优解，C=1.36×105，g=32.59。

基于最小二乘法拟合两个参量的关系式：

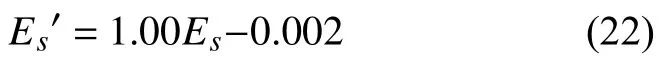
根据式（10）～（13）计算了支持向量机读数结果的线性度、迟滞、重复性和误差（表6）。

表6 基于支持向量机模型的传感器性能指标

经支持向量机融合后，传感器的迟滞和重复性指标比原始数据计算得到的指标及BP算法改善后的指标有较大程度的改善，误差由原始读数模型的减小到了1.9 %。可见，采用小样本学习机理的支持向量机技术，可以建立更为准确的传感器读数模型。

3.3 与其他读数模型结果的对比

为了与其他智能算法的效果进行对比，优化电场传感器的检测指标，本文还采用了径向基神经网络和遗传神经网络来优化传感器的性能。5种不同方法的误差对比（表7）对比说明，在有限的样本条件下，基于支持向量机的数据融合方法更有效地改善了传感器的性能，消除了电场三维方向的交叉干扰，减少了测量误差。

表7 使用不同建模算法数据融合后传感器误差的对比

本文所用森馥SEM-600低频电磁辐射测量仪输出数据经数据融合后，测量仪线性度及误差指标均优于现有技术（表8），在电场检测领域具有显著优势。

表8 与现有电场传感器性能指标对比

4 结束语

在一个标准电场发生器中对SEM-600三维电场传感器进行了标定。采用最小二乘法对三维电场的检测结果进行了分析，获得传感器的误差为13.6%。检测结果表明，三维电场检测存在交叉干扰。为了消除交叉干扰，提高检测准确度，采用了神经网络、支持向量机等智能算法，对传感器的性能进行了优化。5种方法读数结果的对比表明，在相同的样本数量下，基于支持向量机的读数模型，使电场传感器的线性度和重复性分别从原始数据的4.33%和8.41%，显著提高至0.01%和1.05%，误差从原始数据的13.6%降低至1.9 %，极大减少了传感器的检测误差。