一种基于PCA-BP的直升机起落架着舰载荷评估方法

郑甲宏，赵敬超

（中国飞行试验研究院，陕西 西安 710089）

0 引 言

军用直升机起落架研制在国军标和型号规范中都有具体要求，如GJB 5771—2006《舰载直升机通用要求》中5.3.1描述“直升机起落架系统应充分吸收不小于3.05 m/s相对下沉速度着舰时的冲击能量，不会发生永久变形，1.5倍的上述冲击能量时，结构不会破坏”。因此直升机起落架在进行鉴定试飞考核时，必须测量着舰下沉速度达到飞行包线边界的着舰载荷，考核起落架着舰载荷是否超过其结构的使用设计值，从而给出起落架鉴定试飞结论。

然而，研制的新型直升机起落架在进行大质量，大下沉速度，尤其是包线边界及包线扩展工况下的着舰载荷飞行试验时，起落架必然承受很大的着舰载荷。为了降低试飞风险，国内目前对于起落架着舰载荷的鉴定试飞并没有考核到边界状态，而是采用起落架地面落震试验来评估边界状态的着舰载荷。虽然落震试验尽可能地模拟直升机在飞行试验中的着舰工况，但是由于存在海上着舰环境、起落架与机体的约束、直升机着舰方式、着舰姿态等因素的差异，实际上地面落震试验并不能取代飞行试验。因此，准确地评估起落架的着舰载荷具有重大意义[1-2]。

研究人员尝试采用建立数学模型的方法评估着舰载荷[3-6]。但是，由于模型涉及很多理论假设，且参数之间有很强的非线性关系，数学模型很难得出一个好的评估结果。目前很多研究通过建立神经网络模型的方法来评估飞行载荷。美国海军已经证明了通过飞行参数来评估结构载荷应变的可行性，并成功应用于F-14B的机体载荷应变评估。Cabell R H等[7]通过建立神经网络模型，评估了AH-64A型直升机处于健康监控下的直升机关键飞行部件的交变载荷。在训练过程和测试过程中，评估值和测量值有较高的相关性。

虽然通过建立神经网络模型评估飞行载荷已经可以得到一个不错的评估精度，但是有很多的参数影响直升机部件的载荷模型，而且这些参数之间有很强的相关性，如果将这些影响因素直接作为输入变量应用于神经网络模型，那么评估模型的结构将会非常复杂，容易使模型在训练的过程中陷入局部最小值，通用性也会变得很差。本文采用主成分分析（PCA）与后退式神经网络（BP）相结合的方法建立了评估模型，并对模型进行了验证，取得了较好的效果，提高了直升机起落架着舰载荷的评估精度。

1 PCA-BP模型原理

1.1 PCA基本思想及求解

主成分分析采用一种降维的思想，通过产生几个综合变量，使它们包含尽可能多的原始变量信息，并通过这些选定的变量来解释原始数据中的大部分变化[8-9]。

1）原始数据的标准化

通过下式对原始变量进行标准化：

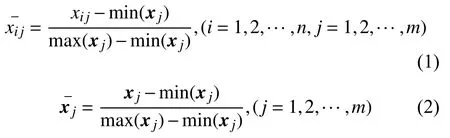
2）计算相关系数矩阵R

相关系数矩阵R可用下式计算：

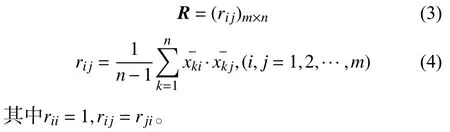
3）计算特征值和特征向量

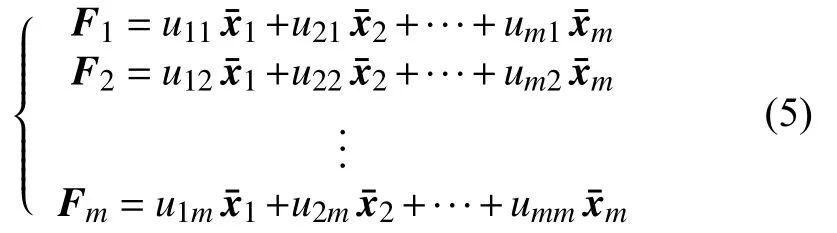
其中，Fm表示第m个主成分。

4）提取p个主成分

计算主成分的贡献率和累积贡献率，根据累积贡献率提取p个主成分，直到特征值的累计贡献率达到90%以上。通过下式可计算出第j个主成分的贡献率bj与累计贡献率ap：

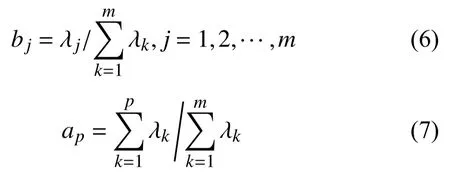
最后，原始样本用p个主成分表示：

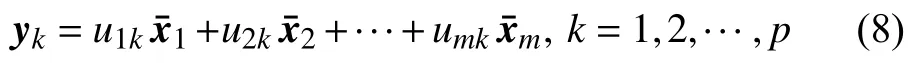
1.2 BP神经网络原理

BP神经网络已迅速发展成为一种重要的数学应用工具，成功解决了多个领域的评估问题。该方法具有强大的自学功能和非线性处理功能，可以不必确定自变量与因变量的函数关系，而是不断地通过自身的学习训练，达到求解复杂工程问题的目的，具有结构简单，易于实现的功能的优点。

BP神经网络结构如图1所示，其中首尾两层分别称为输入层和输出层，中间各层称为隐含层。BP神经网络中各层之间的神经元为全连接关系，层内的各个神经元之间无连接。

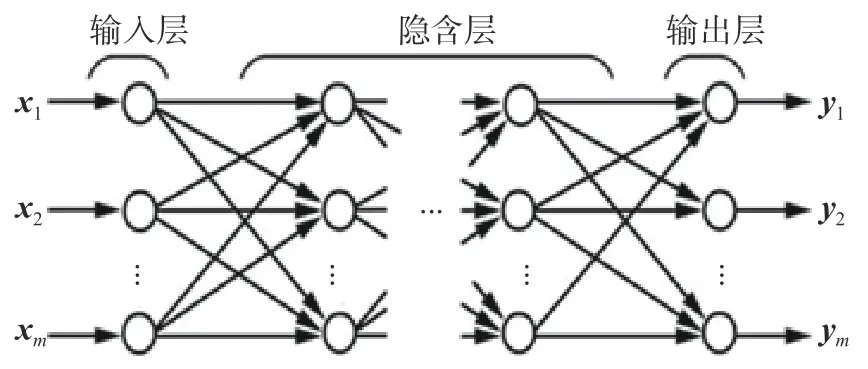
图1 BP神经网络的典型结构

BP神经网络采用有指导的学习方式进行训练和学习，即当一对学习模式提供给BP神经网络后，神经元的激活值从输入层经各个隐含层向输出层传播，在输出层的各个神经元获得网络的实际输出响应。通过比较输出层各个神经元的实际输出与期望输出，获得二者之间的误差，然后按照误差减少的方向，从输出层经各个隐含层并逐层修正各个连接权值，最后回到输入层。这种正向计算输出-反向传播误差的过程不断重复进行，直至误差降低至可接受的范围，BP神经网络的学习训练过程也就随之结束。BP神经网络求解评估问题的算法流程如图2所示[10-11]。

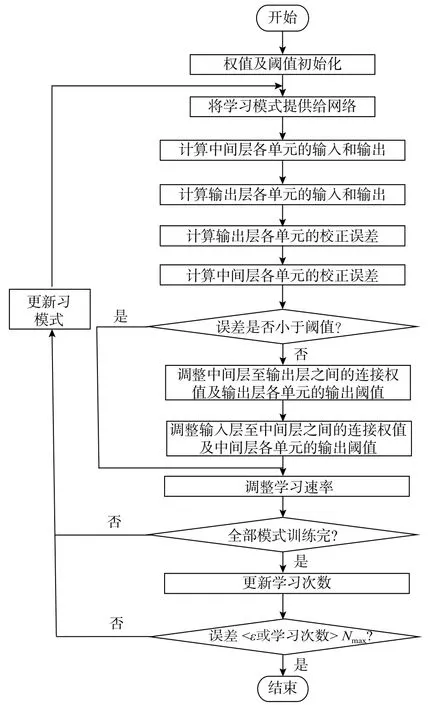
图2 BP神经网络算法流程

1.3 PCA-BP评估模型构建

将累积贡献率达到90%的p个主成分作为BP神经网络的输入变量，并对神经网络模型的参数进行调试，确定满足精度要求的隐含层及其神经元的数量，最终得到PCA-BP模型。将模型的结构及参数保存，即可通过输入变量得到评估值。PCA-BP评估模型流程如图3所示。

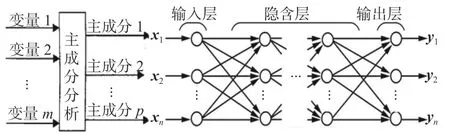
图3 PCA-BP评估模型流程图

2 试验数据的获取

直升机起落架在着舰状态下，其轮轴主要受到垂向的弯矩和航向的剪切作用，摇臂受到弯矩和轴向力，防扭臂受到拉力和弯矩，内筒受到轴向力。为了测量其在着舰过程中的受载情况，在起落架上进行了应变计改装，如图4所示。通过开展地面载荷标定试验，获得了直升机起落架垂向载荷与起落架各部位应变的多元线性关系，即载荷标定方程。通过开展飞行试验，采集直升机起落架着舰载荷过程中对应的着舰姿态、下沉速度、着舰质量重心、发动机参数等飞行状态数据及起落架各部位着舰应变值，将应变值代入载荷标定方程，得到着舰垂向载荷。

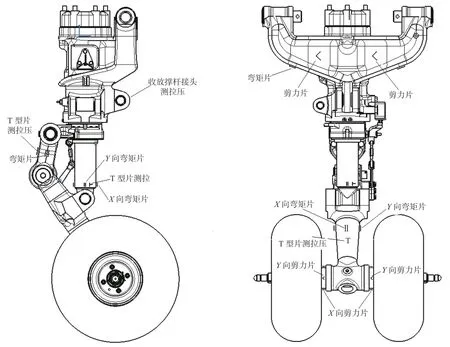
图4 起落架应变贴片位置

3 起落架着舰评估模型的建立与验证

将直升机的14个飞行状态参数：无线电高度、飞行质量、下沉速度、法向过载、横向操纵位移、纵向操纵位移、航向操纵位移、总距角、俯仰角、滚转角、偏航角、俯仰角速率、滚转角速率、偏航角速率进行主成分分析。这些参数可反映直升机起落架着舰时的飞行状态，而且是直升机起落架着舰时主要的飞行监控参数。经主成分分析，每一个变量的方差和所有变量的累计方差如表1所示。一般认为参数的总累计方差达到80%～90%采用主成分分析是有效的。取前4个主成分，其总累计方差为89.786%，这4个主成分可以很好地表达14个飞行参数的内容。它们相互正交，相关系数为0，因而主成分分析达到了降低变量相关性的效果，而且减少了变量的个数，使模型简单化。

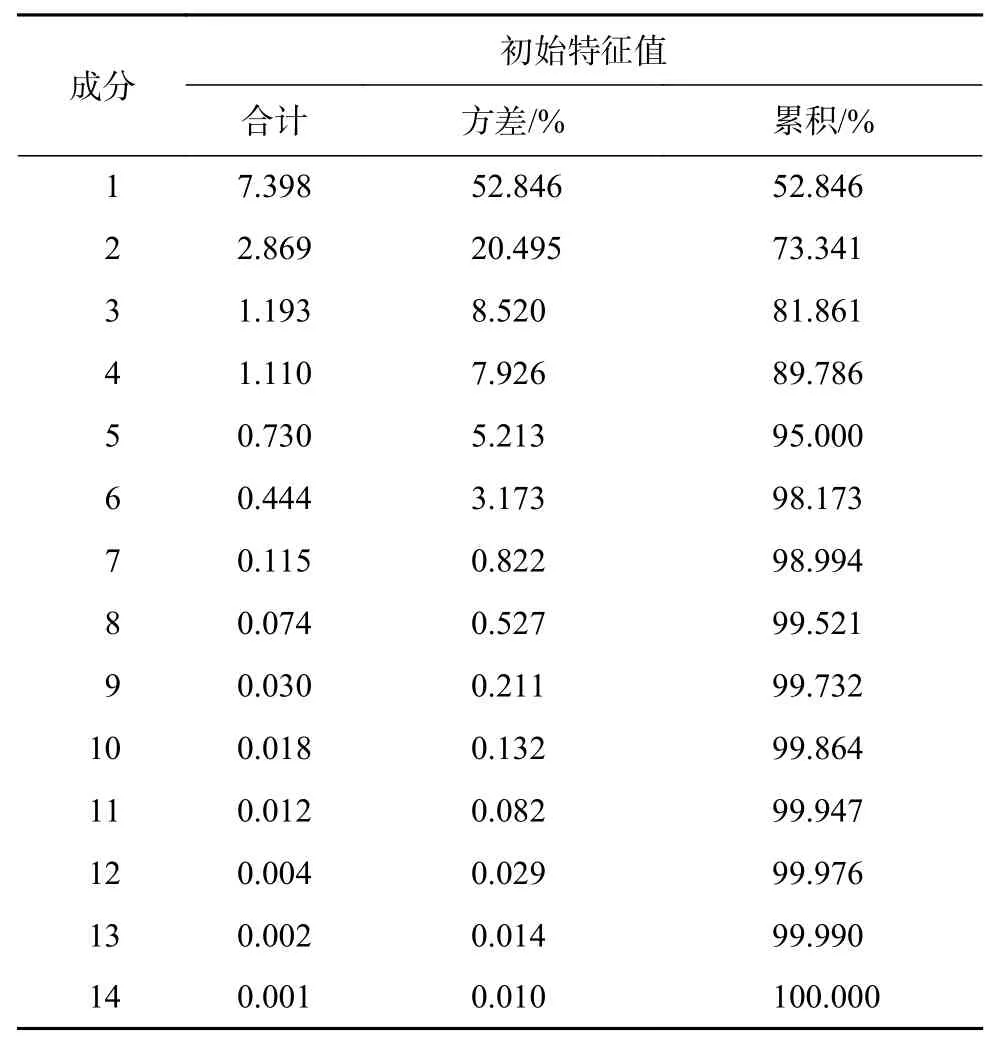
表1 解释的总方差

把这4个主成分作为BP神经网络的输入量，起落架着舰载荷作为BP神经网络的输出量。由于模型的复杂程度一般，所以选择只用一个隐含层的3层神经网络结构，隐含层的转移函数采用sigmoid函数，输出层采用线性转移函数，并采用Levenberg-Marquardt函数最优化算法来训练神经网络，目标误差设定为0.01，学习效率设定为0.01。BP神经网络的输入层包含4个神经元，输出层包含1个神经元。隐含层的神经元数目对整个模型的容错能力具有重要的影响，其个数m可由经验公式得出：

式中：A——输出神经元数量；

B——输入神经元数量；

C——1～10之间的常数[12]。

采用试凑法对不同隐含层神经元数目的网络模型进行训练，经过多次调试，当隐含层m=6时，其输出误差最小。从而BP神经网络的模型结构为4×6×1。利用Matlab软件进行建模及测试。模型数据分为训练集和验证集两部分。其中训练集占总样本的比例为90%。采用均方根误差RMSE和拟合优度r2作为旋翼桨叶挥舞载荷评估的误差评价指标，其表达式为

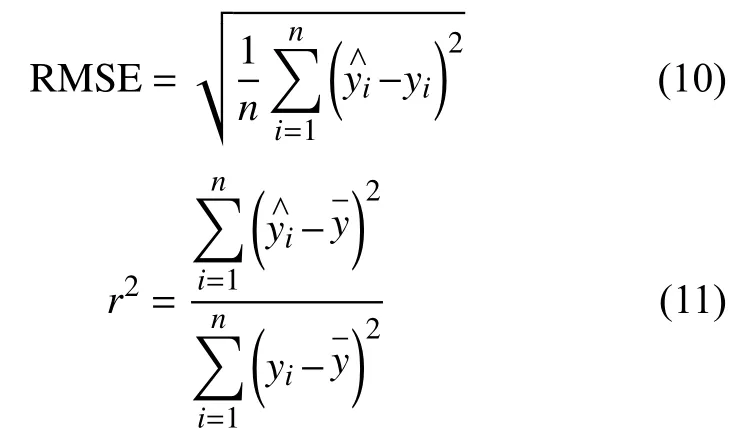
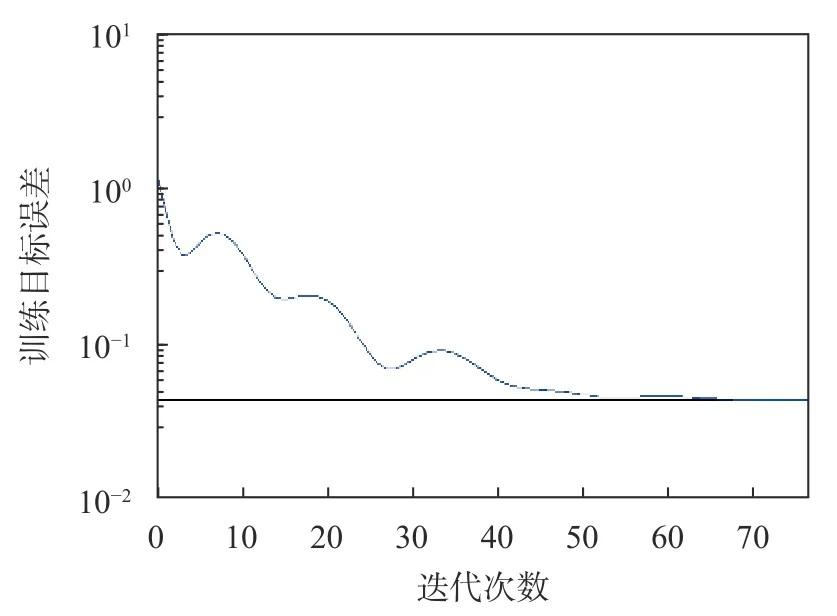
图5 PCA-BP模型训练样本误差输出曲线

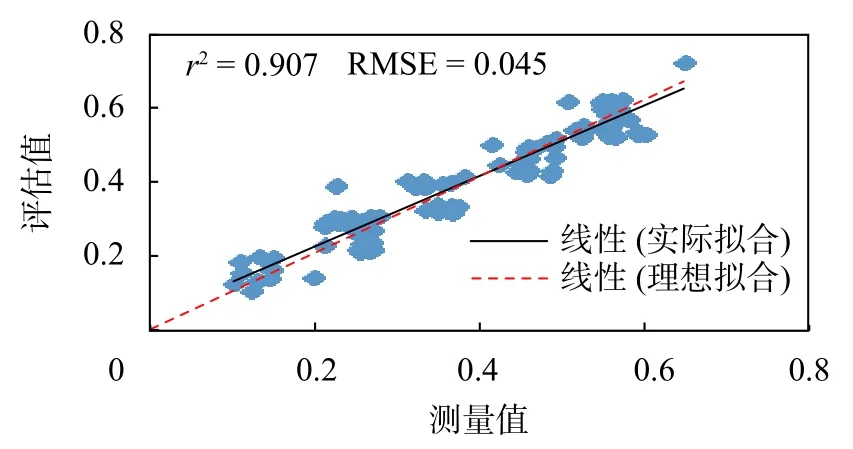
图6 PCA-BP模型验证样本评估值与测量值对比

为了进行模型的对比分析，在BP神经网络训练中，把14个飞行状态参数直接作为输入变量，起落架载荷作为输出变量，进行全要素的BP神经网络训练，模型的训练数据、验证数据及模型参数的选取方法同PCA-BP模型。全要素BP神经网络的训练样本的误差输出曲线如图7所示，验证数据的输出结果如图8所示。

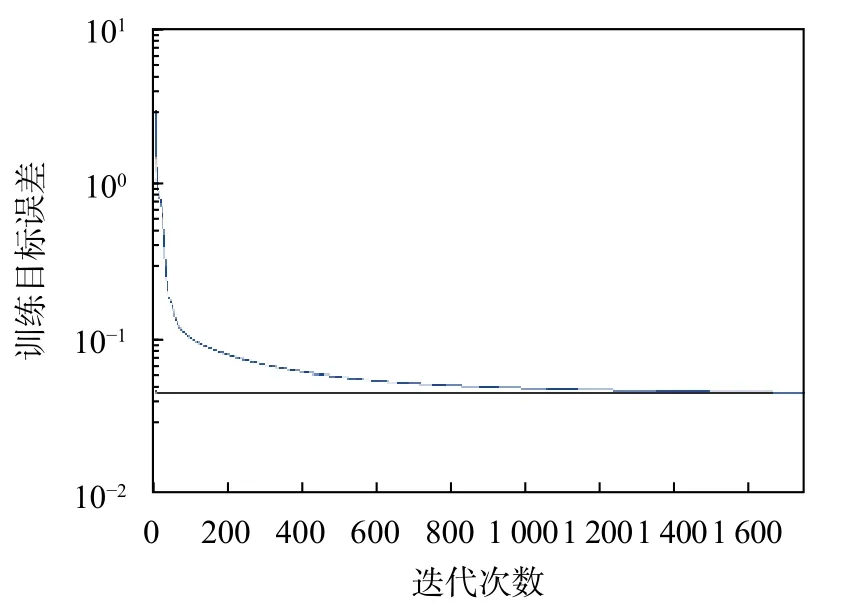
图7 BP模型训练样本误差输出曲线

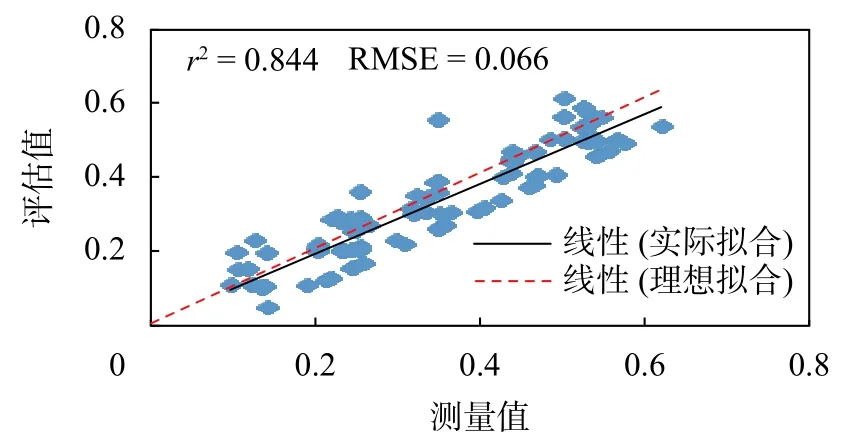
图8 BP模型验证样本评估值与测量值对比

从图5和图7模型训练样本的误差输出曲线可以得出，欲达到同一期望误差精度0.045，BP神经网络模型需要训练1 623步，而基于PCA-BP模型只需要67步。可见，PCA-BP模型具有更快的收敛速度。从图6和图8可以得出，BP神经网络模型的拟合优度r2为0.844，均方根误差RMSE为0.066，而PCA-BP模型其拟合优度r2为0.907，均方根误差RMSE为0.045。可见，PCA-BP模型具有更高的精度。

4 结束语

本文提出将主成分分析和BP神经网络相结合进行直升机起落架着舰载荷的评估，对影响着舰载荷的飞行状态参数进行了主成分分析，其结果作为BP神经网络的输入数据，克服了自变量间的多重共线性问题，减少了输入变量的个数。结果表明，PCA-BP模型相比于全要素BP神经网络模型精度更高，收敛速度更快。