一种投影数据恢复的扇束CT局部重建算法

梁亚星，张 权,，张 萌，陈 燕，桂志国,

（1.中北大学 电子测试技术国家重点实验室，山西 太原 030051; 2.中北大学 生物医学成像与影像大数据山西省重点实验室，山西 太原 030051; 3.中北大学信息与通信工程学院，山西 太原 030051）

0 引 言

X-ray计算机断层成像技术（CT）是一种重要的现代医疗诊断手段，在疾病的早期筛查和后续的诊断治疗等方面发挥着重要作用。新型冠状病毒肺炎（COVID-19）传染性强、潜伏期长。而高分辨率胸部CT敏感度高，能检测出毫米级病灶[1]，目前国家卫生健康委员的诊疗方案中已将CT作为诊断COVID-19的常规首选影像学手段。

鉴于同一患者在诊断过程中往往需要进行多次CT复查，且大多数患者免疫力降低，不宜接受过多的X线辐射[2-3]，故在扫描过程中降低X射线剂量是有必要的。基于感兴趣区域的局部断层扫描成像技术由于可以较好地控制辐射剂量，因而在临床治疗中具有应用推广价值。该技术在扫描过程中仅覆盖可疑的病灶部位，避免了对正常区域的不必要射线照射，同时硬件设备的运行损耗也得到降低。但由于采用局部扫描的方式，投影数据被截断，在重建的局部图像边界存在高亮的圆环，且含有灰度移位伪影，从而降低了重建图像的质量。

为有效消除截断伪影，传统方法在扩充缺失数据时多将投影数据进行外插延拓，基本思想是依据某一投影角度测量的已知投影数据对截断投影数据进行扩充。其中，陈云斌[4]、王克军[5]将某一投影角度下处于边缘的两个投影数据作为常数，分别向两侧扩充，直至填充整个数据区域；薛少峰[6]利用截断数据边界内已知的若干连续投影数据进行曲线拟合，并根据该拟合曲线值向外插值，获取缺失的投影数据。此外，王浩[7]则是根据截断投影数据相邻部分的已知投影数据，利用级比生成法扩充缺失数据。

此外，近年来深度学习由于其强大的图像特征提取能力，逐渐被应用于提高低剂量CT图像质量[8-11]。其中，Li等[10]对于密集和稀疏角度采样的截断投影数据，提出采用神经网络拟合FBP过程，实现了CT的精确重建；王蕾[11]则利用深度生成网络预测不完全投影数据的缺失部分，进一步重建图像。同时，深度学习处理图像的效果往往也受限制于低剂量CT图像质量退化程度、训练样本数目以及算法的计算复杂度，相比较之下，传统的局部重建方法重建速度较快，应用范围较广，仍然具有较大的研究价值。

为此，受文献[12]基于线过程模型的平滑性约束集投影重建图像，文献[13]根据变分偏微分方程实现图像修复启发。基于截断投影数据的特点，以及线过程模型描述图像的边缘结构特性，本文将线过程模型和全变分模型引入截断投影数据恢复过程中，提出了一种新的局部重建算法。

1 算法的引出

图1 局部重建的投影数据

故对截断数据进行恢复时，需要依据已知的A部分投影数据外推截断边界以外的B部分投影数据。全变分模型最初应用于图像去噪，后被逐渐应用于修复不同程度的破损图像，因截断数据恢复过程本质上也是一个借助待恢复区B的邻域信息A恢复较为完整的投影数据问题，本文研究了将全变分模型用于恢复截断投影数据的有效性。

由于待恢复投影数据点存在邻域数据缺失的问题，利用全变分模型恢复截断数据时存在不足，需要合理利用已知的投影数据值对待恢复数据值的邻域进行预插值。

2 本文算法

算法的基本思想包括两部分：根据已知的截断投影数据预估待修复点邻域的投影数据；将线过程模型检测出的截断数据边缘信息作为恢复截断数据过程中的扩充边界，并利用全变分模型恢复缺失的投影数据。基于恢复后的投影数据，进一步滤波反投影重建得到CT局部图像。

2.1 联合线过程和全变分模型的截断投影数据恢复

2.1.1 边缘检测

其中阈值Th决定线过程对于投影数据边缘的敏感度，阈值小，则被判断存在线过程的区域越大，对截断投影数据的边缘信息保存就越多。

故在利用全变分模型对截断数据进行扩充过程中，需要对判定线过程区域的阈值Th进行自适应调节。在扩充过程的起始一段时间，阈值设置较大，以便快速获取截断数据的边缘位置，此时依据全变分模型扩充后的投影数据值较小；自适应调节阈值大小，经过一定迭代次数后，使得经由全变分模型扩散的投影数据与截断数据边界处的投影数据值逐渐接近，从而达到截断数据恢复的目的。

2.1.2 全变分模型用于投影数据恢复的存在问题

根据偏微分方程理论中的热传导数学模型，将投影数据的灰度值视为平面物体的温度，则投影数据恢复过程，可视为由截断数据邻域已知的投影数据作为固定点提供热量的热传递过程。由于全变分图像修复模型采用各向异性的信息扩散方式，可以较好地保护边缘特征和细节信息。因此，在获取截断投影数据的边界位置后，采用全变分模型扩充缺失的投影数据。

全变分模型修复图像的代价函数为

运用Language乘子法将有约束的极值问题转化为

式中：r——正的实函数；

u——图像的像素值；

λ——Language乘子。

引入时间量t，采用梯度下降法求解，则得到最速下降方程为

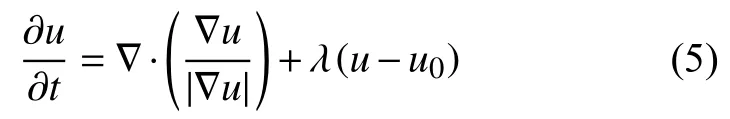
其中∇·、∇分别代表散度和梯度算子。

根据Euler-Lagrange方程，将偏微分采用差分代替，引入半点中心插值法求解函数u。若采用3×3像素邻域，则获得求解公式如下：

其中已知投影数据待恢复点o周围的四邻域像素点、四邻域半像素点，求解过程中循环次数、平滑系数和步长采用控制变量法，经过多次实验确定投影数据恢复的参数最适值。因局部扫描下投影数据不完整，待修复的像素点处于边界位置时，其3×3像素邻域的部分像素点是不完整的，无法直接利用公式（6）进行求解，故应合理利用已知的投影数据值，对待修复点的邻域点进行预插值。

2.2 待恢复点邻域预插值

由于待恢复的投影数据灰度值仅与其邻域内像素有关，与较远像素位置无关。全变分恢复过程采用3×3像素邻域时，需充分利用邻近的截断投影数据灰度值，对待恢复点像素的邻域点进行预插值。

假设ui,j为一个待恢复点，m为待恢复投影数据所在的探测器位置，如图2所示。由于第m、m-1行探测器投影值为零，采用3×3像素邻域恢复中心像素点ui,j时不免代入零值，降低数据恢复的效率，故第m-1行探测器的数据值将通过第 m+1行已知的3个投影灰度值加权获得，即

图2 待恢复点ui,j及其邻域

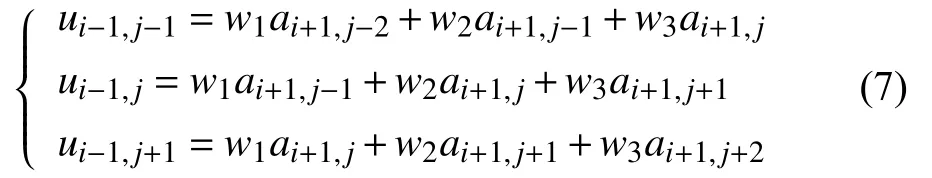
其中权重wi根据待插值点ui与已知点u0的欧氏距离比确定，即

对待恢复点ui,j的3×3像素邻域仍存在的未知投影数据值ui,j+1，可通过上次全变分模型恢复的投影数据值ui,j-1等值估计，即

到此，待恢复点 ui,j的3×3像素邻域点已完成预插值，则可根据全变分模型的公式（6），求解待恢复点ui,j的投影数据值。则基于全变分框架的截断投影数据恢复算法框图如图3所示。

图3 基于全变分恢复截断投影数据的局部重建算法

综上所述，所提算法具体步骤如下：

1） 截断数据获取：将Shepp-Logan体模进行360°全局扫描，得到图4（a）所示完整的投影数据，对完整数据截断得到局部的扫描数据，如图4（b）所示；

2） 投影数据边缘检测：根据公式（2），利用线过程模型检测出的截断投影数据的边缘信息作为扩充条件，图4（c）为截断投影数据垂直方向的线过程，即检测到的待恢复投影数据的边界位置；

3） 待恢复点预插值：在此基础上应用公式（7）、（9）对待恢复点像素的3×3像素邻域点进行预插值；

4） 应用公式（6）对截断投影数据进行恢复，恢复后的投影数据图4（d）所示；

图4 仿真模型投影数据算法过程图

5） 依据恢复后的投影数据，经滤波反投影重建得到CT局部重建图像。

3 实验结果与分析

实验中，采用Shepp-Logan头部体模和实际骨盆数据，选取以图像中心为圆心、半径为50像素圆形区域为待重建感兴趣区域，重建图像为256像素×256像素，验证算法进行局部重建的可行性。

为了进行对比验证，将截断数据分别进行常数延拓、对称延拓，并重建图像。其中，常数延拓将截断投影数据上、下边缘处的投影数据作为常数向两侧扩充；对称延拓则是以截断数据边界处的数据作为对称点，以对称的方式，分别对上、下边界之外的缺失数据进行扩充。

此外，为了定量评价算法的有效性，采用归一化均方距离判据NMSD、归一化平均绝对距离判据NAAD、均方误差MSE、峰值信噪比PSNR和结构相似性SSIM进行进一步验证：

式中：ui,j和vi,j——原始图像和重建图像第i行、j列的像素灰度值；

μu和μv——原始图像和重建图像的平均灰度值；

σu和σv——原始图像和重建图像的标准差，图像的像素为N×N个。

3.1 仿真数据实验

实验采用256像素×256像素的Shepp-Logan仿真模型。采用等角度扇束扫描，投影角度数为360个，探元数目246个，选取中间68个探元数据作为截断投影数据。图5（a）、（b）分别是原始体模及其ROI放大显示图。

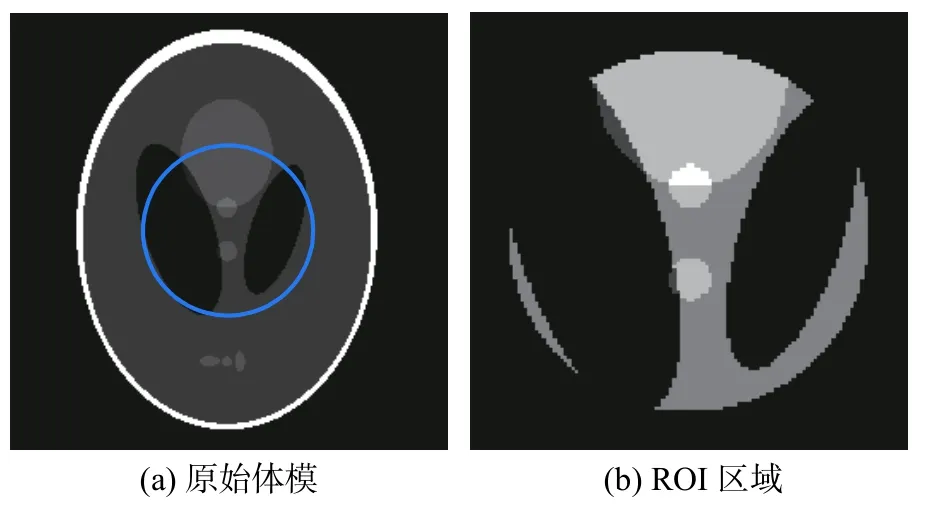
图5 仿真模型

图6左列为截断数据，以及截断投影数据经常数延拓、对称延拓和本文算法三种算法扩充后FBP重建结果，右列分别为局部重建结果分别与原图相应的感兴趣区域图5（b）的差值图。显然，截断数据局部重建图6（a）和对应差值图6（b）的边界处都存在环状的高亮截断伪影，且重建图像灰度值产生畸变，边界区域像素的灰度值偏高。与其他截断数据扩充后的FBP局部重建图比较，本文算法重建图6（g）抑制了边界处的环状截断伪影，且图像的对比度提高、均匀性较好。比较重建图像差值图，可以看出图6（b）、图6（d）和图6（f）的左下角方框区域内存在部分程度损失的边缘信息，相比之下图6（h）中的边缘残留更少，进一步说明本文算法重建局部图像的边缘结构信息保存的更加完整。

图6 左列为不同算法FBP局部重建图，右列为ROI差值图

为了更加客观评价本文算法，表1列出了各局部重建算法定量评价参数。分析比较可见，本文算法的NMSD、NAAD和MSE值较低，表明重建图像与ROI差异程度小，PSNR值较高表明失真程度小，SSIM数值表明本文算法局部重建图像与ROI的结构相似程度高，从而验证了本文算法恢复截断投影数据的有效性。

表1 仿真数据经不同算法恢复后的局部重建图像定量评价参数

3.2 实际数据实验

为了进一步验证算法的实用性，实验采用实际骨盆数据。投影角度数360个，探元数目512个，选取中间180个探元数据为截断投影数据，如图7所示。

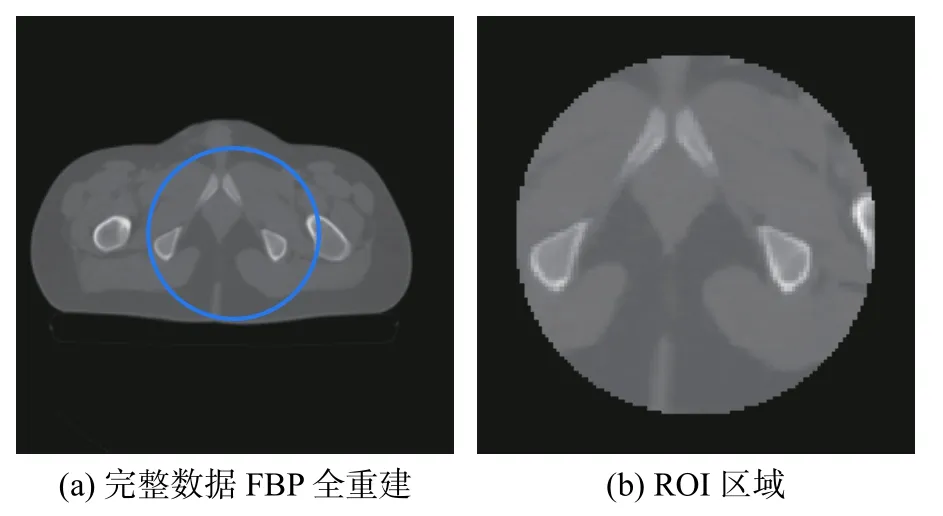
图7 实际骨盆

图8（a）、（b）分别为完整投影数据和截断投影数据，图8（c）为采用本文算法恢复后的投影数据。

图8 实际骨盆投影数据

图9左列为截断投影数据经不同算法扩充后FBP重建结果，右列为对应差值图。图9（a）、（b）的边界处都存在环状亮伪影，这与仿真模型截断投影数据的局部重建结果边界处存在的高亮环状伪影相一致。将局部重建结果图与感兴趣区域图7（b）比较，图9（e）的矩形框标注内存在明显的图像信息缺失，上下边界处重建效果较差，这在定量评价参数中也得到体现。而本文算法局部重建图像图9（g）的边界处环状截断伪影得到抑制，视觉效果比较好，对比差值图9（h）也存在更少的细节信息。

图9 重建图与插值图（左列为不同算法FBP局部重建图，右列为ROI差值图）

图10为对应算法局部重建结果图与完整数据重建图像ROI的结构相似索引图。比较图10（a）～（d），本文算法处理的图10（d）矩形框标注区域内的像素亮的程度比较高，进一步表明本文算法重建的局部图像质量较高。

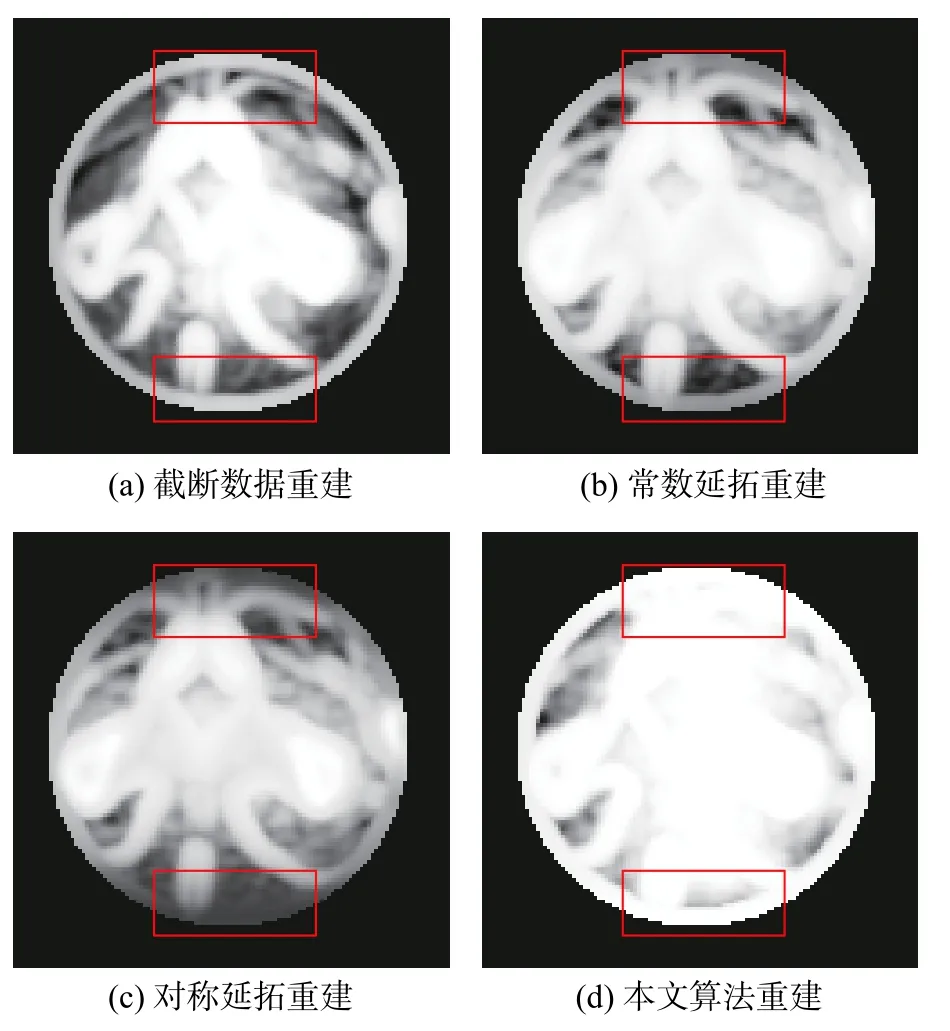
图10 不同算法重建图的结构相似索引图

表2列出了局部重建算法定量评价参数，与其他截断数据扩充方法比较，本文算法NMSD、NAAD和MSE值降低，PSNR值和SSIM值有明显的提高。本文算法局部重建图像的有效性进一步得到了验证

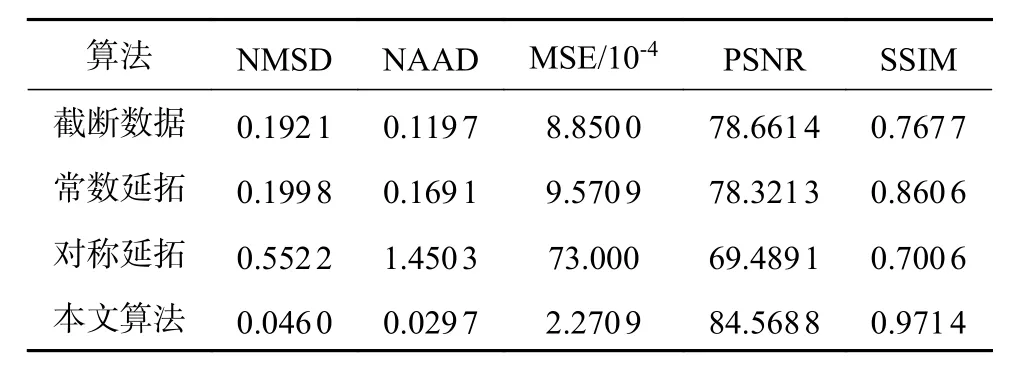
表2 实际数据经不同算法恢复后的局部重建图像定量评价参数

4 结束语

本文提出了一种基于投影数据恢复的扇束CT局部重建方法。利用线过程模型检测的截断投影数据边缘信息作为扩充边界；在恢复过程中，针对待恢复点像素的邻域点的数据缺失问题，利用已知投影数据的距离比加权进行预插值，然后依据全变分模型对中心投影数据值进行恢复，改善了直接使用截断数据重建图像造成的截断伪影问题。对比其他截断投影数据扩充方法，从仿真数据和实际数据的局部重建图像的视觉效果及客观评价参数等方面，评估了算法的可行性。