金属疲劳损伤的线性与非线性超声联合评价方法研究

周 崎，刘莹峰，樊嘉琦，李 浩，黄嘉诚

（1.广州海关技术中心，广东 广州510623; 2.南昌航空大学 无损检测技术教育部重点实验室，江西 南昌330063）

0 引 言

金属材料被广泛应用于实际工程应用中，而在役工件在长期经受交变载荷后极易产生疲劳损伤。从位错和驻留滑移带等微缺陷的产生到宏观裂纹的形成一般占材料疲劳寿命的80%以上，故及时发现材料微观结构变化和微裂纹萌生，可有效减少因结构突然失效造成的灾难性后果[1]。现有的超声无损检测技术利用波的时程、声速和衰减等线性物理参数己经可以对构件寿命的第二和第三阶段进行有效的检测和评估[2]。而作为线性超声检测的超声波衰减系数法，具有检测材料疲劳后期产生内部空隙与微裂纹的优点。但是，线性超声技术很难发现材料早期性能退化过程中微观组织结构变化及微小缺陷[3-5]，更适用于开放式裂纹或者声阻抗差异较大的夹杂等缺陷检测[6]。而非线性超声本质上反映的是微小缺陷对材料非线性的影响，检测的特征参数并不受限于缺陷和损伤的大小[7]。超声非线性系数的变化对材料早期微观结构变化非常敏感，难以对于后期疲劳损伤进行定量评估。

近年来，国内外学者基于金属材料的超声非线性研究越来越多，并且取得了一些成果。RAO[8]通过对不同疲劳状态下铝合金的纵波传播特性进行研究，得到超声非线性参数的变化与材料疲劳状态密切相关。师小红等[9]测试不同阶段下微裂纹扩展的非线性参数，得出非线性参数与材料疲劳寿命对应关系，从而实现对金属构件剩余寿命的预测。阎红娟等[10]基于传统的疲劳位错累计理论，提出了二阶和三阶非线性系数的位错模型，基于概率分析将位错综合模型用于金属构件疲劳寿命的预测。对于衰减系数评价疲劳损伤，朱茂鸿[11]通过对铝合金疲劳损伤研究，发现超声衰减系数可以反映材料的损伤程度。董志勇等[12]通过高温拉伸试验发现超声衰减在材料损伤过程中与时间呈一定的正相关性。

鉴于超声衰减系数对于检测材料损伤以及裂纹扩展的优越性，却难以评估材料早期性能退化的过程，而非线性超声检测技术对材料早期疲劳时的微观缺陷较敏感，但对材料疲劳寿命后期难以进行准确评价的缺点。本文通过对比试验的方法探究了Q345钢材料早期疲劳损伤对超声非线性效应与超声衰减的影响，得到了非线性参数、衰减系数与疲劳寿命的关系曲线（α-β-N曲线），用该曲线对金属材料疲劳损伤进行联合评价，并验证该曲线的表征能力。

1 超声非线性效应理论与超声衰减检测方法

1.1 非线性超声检测基本理论

二次非线性超声纵波在各向同性介质传播，其简化的一维波动方程为

式中：ρ——材料密度；

u——质点位移；

x——声波的传播距离；

σxx——x方向的法向应力；

t——传播时间。

二次非线性本构方程为

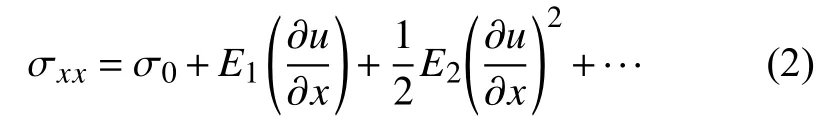
其中E1、E2分别为二阶、三阶弹性常数。则非线性波动方程可以写为

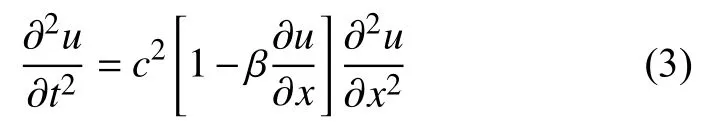
式中：β——非线性系数；

c——介质中纵波声速。

对于处于初始状态的材料，β是晶格的非简谐分量，β0为材料二阶、三阶弹性常数的方程

式中：C11、C111——二阶、三阶 Brugger常数；

σ0——材料的初始应力。

由于二阶弹性常数与初始应力相对较小，故疲劳载荷主要对三阶弹性常数C111产生影响，从而使非线性系数发生改变。上式为超声波的波动方程在各向同性材料中的精确解。

由上述理论推导可得

通过β′的大小变化来表征材料早期的力学性能退化从理论基础上来说是可靠的。所以本文将采用实验测量倍频信号幅值与基频信号幅值的平方的比值来反映二阶非线性系数β0。

1.2 超声衰减检测基本理论

超声波在固体介质中传播时，由于固体介质材料中的组织影响使得声波在传播过程中会产生发散，反射，折射，吸收等情况，导致接收到超声波信号的幅值大小发生改变。

对于本文使用的薄板工件，探头放置在薄板两侧，上下底面相互平行，故只需计算衰减系数α来表征材料中超声波传播的过程。可以按照下列公式进行计算：

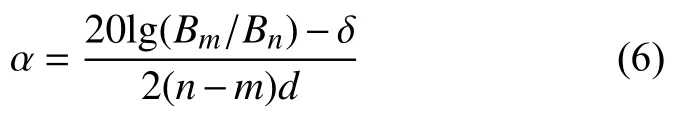
式中：m，n——底波的透射次数；

Bm，Bn——第m，n次透射波高度；

δ——反射损失，每次反射损失约为0.5～1 dB；

d——板的厚度。

超声在介质中传播时，会发生介质衰减和反射损失，所以超声衰减与介质的性质密切相关。当金属材料疲劳损伤引起内部组织发生变化时，将导致底波幅值发生变化，从而引起衰减系数的改变。因此衰减系数能够有效反映疲劳损伤的程度。

2 试样制备

选择厚度均为10 mm的3块Q345钢平行试件，其屈服强度在345 MPa左右，弹性模量为206 GPa，泊松比为0.3，抗拉强度在460 MPa左右，材料密度为7 850 kg/m3。编号为 1#、2#、3#，其中 1#和 2#试件做对比试验，3#试件进行验证实验。其疲劳试样结构示意图如图1所示。

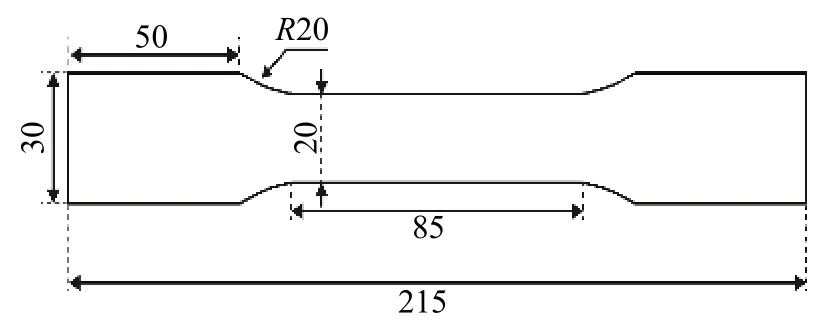
图1 疲劳试样结构示意图（单位:mm）

采用最大载荷为500 kN的Instron伺服万能试验机，对上述板状试样进行室温状态下的拉伸疲劳试验。设置正弦波频率为15 Hz，应力比为0.28。单次疲劳时循环次数10万次，总疲劳次数在1.2×106左右。

3 实验研究

3.1 实验系统搭建

检测系统以SNAP-RAM-5000高能超声发射接收仪为核心，具有ch1、ch2两个独立的输入通道，其工作频率250 kHz～30 MHz，最高可激发功率为5 kW且周期、波形可调的高能射频脉冲信号。试验采用纵波穿透法的检测方式，激励探头的中心频率为5 MHz，接收探头中心频率为10 MHz，探头通过医用超声耦合剂耦合在Q345钢试件薄板上。基于SNAP-RAM-5000高能超声脉冲发射仪，搭建了如图2和图3所示的检测系统，输出端口连接50 Ω阻抗匹配、可调节衰减器和5 MHz低通滤波器将有限振幅的激励信号经过滤波处理后输出至激励探头；信号通过待测试样由接收探头接收后，再利用BNC三通接头传送给ch1、ch2接收通道分别接收，ch1通道直接接收幅值较高的基波信号，ch2通道接收通过10 MHz高通滤波器和有源信号放大器的高次谐波信号。仪器内部对接收到的ch1、ch2通道信号进行傅里叶变换，最终将时域信号转换为频域信号在计算机中显示出来。

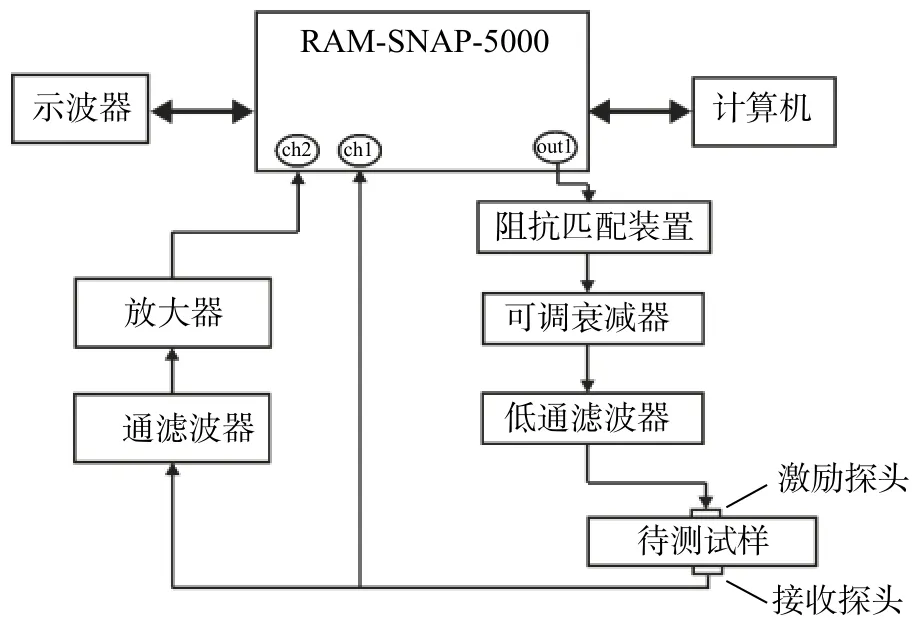
图2 非线性超声检测系统结构示意图

图3 系统实物图

3.2 检测结果及分析

对原始状态试样在288 V激励电压下时的检测时域信号及其频谱图如图4所示。图4（a）中时域信号包含两个波包，两波包分别为直入射波和二次透射波。以两个波包峰值为基点，两波包峰值时间间隔约为3.3 μs，是超声波穿透试块厚度所需时间的2倍，将两次回波幅值按式（6）计算其衰减系数。图4（b）为截取直入射波包的频谱分布图，其基波与二次谐波的最大幅值分别位于5 MHz和10 MHz附近，其相对非线性系数按式（5）计算。

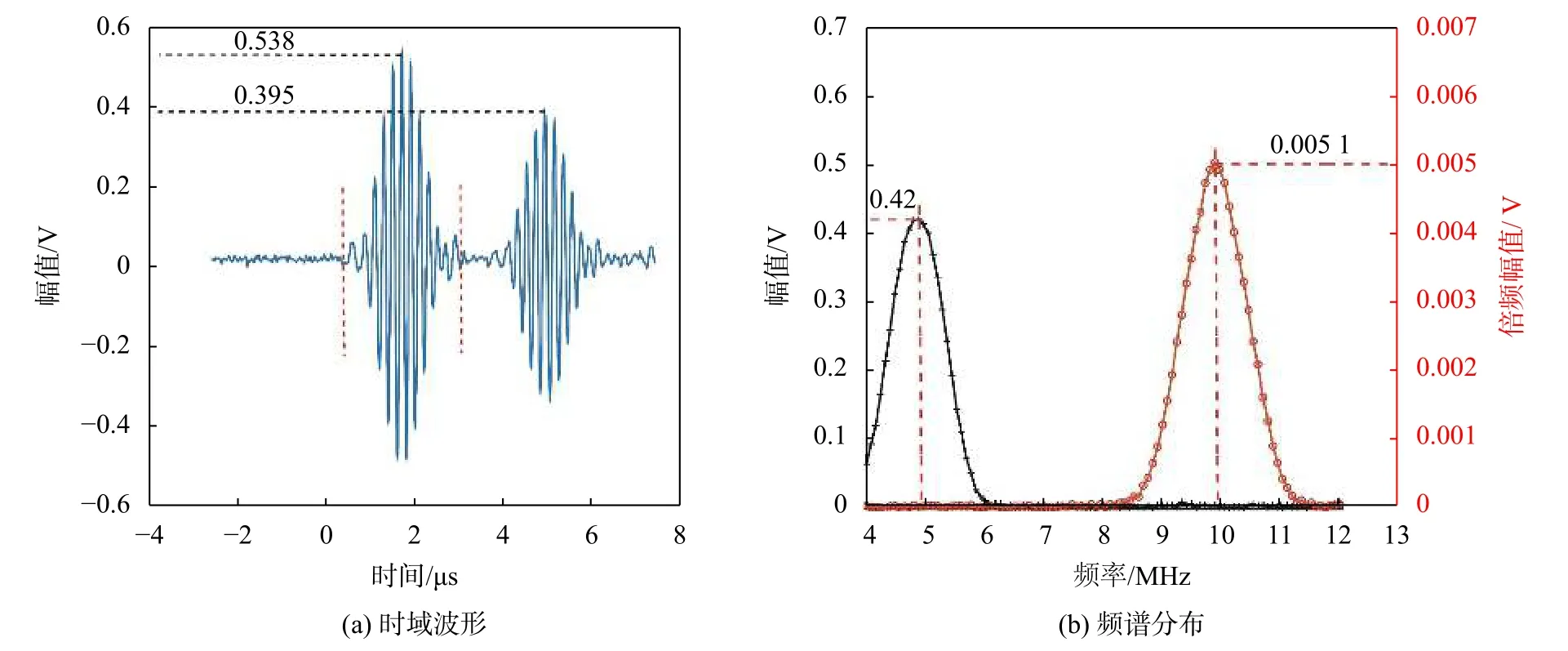
图4 原始状态试样的检测信号分析

疲劳试样的α-β-N曲线如图5所示，图中纵坐标为归一化的相对非线性系数β和归一化衰减系数α（注意两者的量纲是不同的）；横坐标以疲劳寿命的百分数表示，即试样不同循环加载周次与出现宏观裂纹时加载总周次的比值，此曲线为α-β-N曲线。

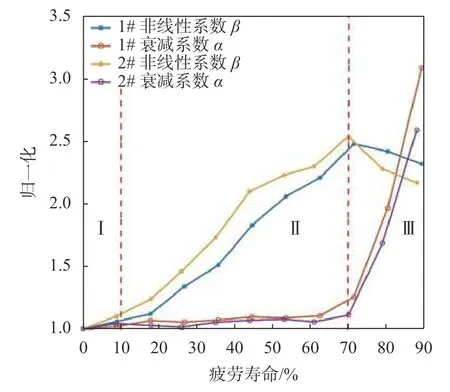
图5 1#和2#试件α-β-N曲线

从图5所示的实验结果可以发现，疲劳程度可以分为3个区域：

1）区域Ⅰ为疲劳寿命0～10%，在此区域内β值增长较缓慢，α基本保持不变。这是由于在疲劳的开始阶段，材料内部的损伤主要表现为内部开始出现应力集中区域。

2）区域Ⅱ为疲劳寿命10%～70%，在此区域内β值呈现单调递增直到极值；而此阶段α的变化很小，考虑到试验过程中的表面质量和探头耦合等误差，可以忽略此阶段α的变化。

3）区域Ⅲ为疲劳寿命70%以上，在此区域内β值呈现下降趋势；而此阶段α的变化急剧单调增加，与疲劳寿命呈现相对清晰的对应关系。

在疲劳寿命的70%之前，在循环应力的作用下在应力集中部位发生位错累积，非线性系数会随着位错累积而增大，此时非线性系数能够有效对应表征疲劳损伤程度。随着疲劳加载周期的增长，由疲劳损伤微裂纹逐渐扩展生长，导致非线性系数的降低。随着裂纹程度的加大，穿透波的幅值会降低，而穿透波多次通过缺陷后幅值衰减更大。在微裂纹扩展过程中，衰减系数随着微裂纹的生长呈上升趋势。因此当检测区域在疲劳寿命的70%以上时，衰减系数对材料的疲劳损伤程度更敏感。

通过上面的分析可以得出，当β出现峰值时，试样的疲劳寿命在70%左右，当α衰减系数是原始状态的2倍左右时，试件的疲劳寿命在80%左右。

为讨论上述评价规律的可行性，实验在相同的条件下对3#试件开展了验证实验。在实验过程中，每加载10万次对试块进行一次非线性系数和衰减系数的测量和计算，测得归一化非线性系数达到极大值时，加载次数达到9×105；归一化衰减系数为2.13时，此时α衰减系数是原始状态的2倍左右，加载次数达到106。根据α-β-N曲线的评价规律，可以认为3#试样疲劳加载次数达到9×105时，疲劳寿命为70%左右；当疲劳加载次数为106时，疲劳寿命为80%左右。将3#试样继续进行疲劳实验直至拉断，得到总的疲劳加载次数为1.26×106即为3#试样的总疲劳寿命。由此可以认为，试样疲劳加载次数为9×105时，疲劳寿命为71.43%；当疲劳加载次数为106时，疲劳寿命为79.37%，图6所示为3#试样的α-β-N曲线。实验结果表明，可以通过该规律对试样进行疲劳寿命的评价及预测。

图6 3#试件α-β-N曲线

4 结束语

1）利用该非线性超声纵波测量系统建立了二阶超声非线性系数与疲劳加载次数的对应关系，超声非线性系数随疲劳加载次数的增加呈先增大后减小的趋势。

2）从α-β-N曲线可以看出，在材料疲劳寿命70%之前，非线性参量可以对应表征疲劳寿命；在疲劳寿命的70%之后，非线性参量呈下降趋势并不能表征材料中裂纹的扩展，而这一阶段α衰减系数显著增长，可以对这一阶段疲劳寿命进行补充评估。实验结果表明，疲劳试样的α-β-N曲线规律可对金属材料进行疲劳寿命预测。