翻斗式雨量传感器重复性试验统计处理方法

邓 超，徐海峰，苏 南，林 薇

（水利部水文仪器及岩土工程仪器质量监督检验测试中心，江苏 南京 210012）

翻斗式雨量传感器重复性试验统计处理方法

邓 超，徐海峰，苏 南，林 薇

（水利部水文仪器及岩土工程仪器质量监督检验测试中心，江苏 南京 210012）

测量仪器的重复性是体现测量仪器精密度的主要指标，重复性试验是对翻斗式雨量传感器性能检测的最重要步骤之一，其试验数据的处理在整个检测试验中也是最为复杂的。针对翻斗式雨量传感器精密度检测试验中重复性实验数据的相关统计处理和计算方法，对重复性限这一重要指标的产生及计算方法进行深入地溯源与公式推导，并引用实例对翻斗式雨量传感器重复性试验数据的评定方法做详细阐述。结果表明：使用本方法进行翻斗式雨量传感器精密度检测符合标准，切实可行也十分必要，为提升翻斗式雨量传感器精密度检测工作水平打下基础。

翻斗式雨量传感器；重复性；重复性标准差；重复性限

1 翻斗式雨量传感器重复性试验方法

在翻斗式雨量传感器检测中，重复性限是一项重要的指标，重复性限的大小，体现着雨量传感器测量精密度的高低。在 GB/T 21978.2—2014 《降水量观测仪器第二部分：翻斗式雨量传感器》中[1]，对仪器的重复性要求是：重复性的定量表达采用重复性标准差 Sr。在相同工作条件及规定降雨强度范围内，翻斗计量误差重复性限 r 应不超过 1%，其中r = 2.83 Sr。并规定试验方法分为自身排水量法和注入法，可任选 1 种进行试验。自身排水量法：在室内规定条件下，传感器处于正常工作状态时，在降雨强度为 0.3～4.2 mm/min 范围内，分大（降雨强度3.8～4.2 mm/min）、中（降雨强度 1.5～2.5 mm/min）、小（降雨强度 0.3～0.5 mm/min）3 种降雨强度，分6 次匀速向仪器注入清水，同时用专用计数器对翻斗翻转次数进行计数，翻斗翻转各 10/c（c 为仪器分辨力），采用标准器具测量仪器自身排水量。注入法：在室内规定条件下，传感器处于正常工作状态时，分大、中、小 3 种不同降雨强度向仪器注入清水，重复进行 6 次，记录每次传感器的输出和历时。也就是说，2 种方法都要求重复 6 次试验。同时规定，在试验完成后要计算重复性标准差和重复性限。

2 重复性标准差计算

2.1 重复性

重复性为测量重复性的简称[2]，定义为在一组重复性测量条件下的测量精密度。

2.2 重复性标准差

重复性标准差是指重复性条件下获得结果的标准差[3]，一般以实验标准差表示[4]。在重复性条件下，由被评定测量仪器对给定的约定真值或稳定的被测量进行连续多次的测量或比较，有时则由提供约定真值的测量仪器对被评定的测量仪器进行连续多次的测量，用实验标准差表示被评定测量仪器的重复性[5]。

2.3 实验标准差

实验标准差为实验标准偏差的简称[6]，是指对同一被测量进行 n 次测量，表征测量结果分散性的量。实验标准差一般用贝塞尔公式计算。

1）n 次测量中某单个测得值 xk的实验标准差S ( xk) 可按贝塞尔公式计算：式中：xi为第 i 次测量的测得值；n 为测量次数；x为 n 次测量所得一组测得值的算术平均值。

3 重复性限计算

3.1 重复性临界差

重复性临界差是指一个数值，在重复性条件下，2 个测试或测量结果的最终值的绝对差以一定的概率小于等于此数。

最终值的例子包括结果序列的平均值或中位数，而序列本身可能含有 1 个或多个结果。

3.2 重复性限

重复性限是指定概率为 95% 的重复性临界差，在重复性条件下，2 个测试或测量结果的绝对差小于或等于此数的概率为 95%[7]。

3.3 重复性临界差来源

3.3.1 平均值原理

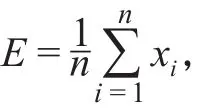
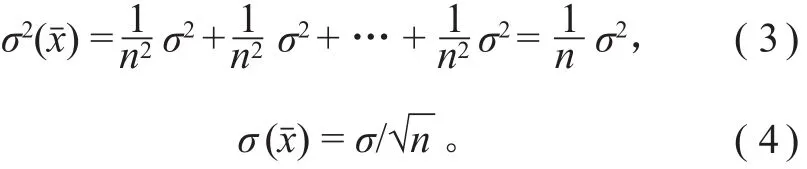
3.3.2 重复性临界差计算

一个估计量是 n 个独立估计量的和或差，每个估计量的标准差均为 σ，则和或差的标准差为重复性限 r 和再现性限 R 均为 2 个测试结果之间的差，因而相应的标准差为

在常规的统计工作中，为了检查 2 个测试或测量结果之间的差异，往往用这个标准差的 Z 倍作为临界差。临界差系数 Z 的值依赖于与临界差相应的概率水平及测量结果所服从的分布。对于重复性限和再现性限，概率水平规定为 95%。在准确度（正确度与精密度）的分析中，对于标准正态分布 N（0，1），查标准正态分布表 φ (x) 可知，概率 P（Z ≤1.96）= φ（1.96）= 0.975。正态分布情况下置信概率 P 与 Z值关系如表 1 所示。

表 1 正态分布情况下置信概率 P 与 Z 值关系表

一般假定基本分布近似正态。在实际中，当标准差的真值 σ 未知时（不能进行完全精密度实验），只能基于有限次的测试或测量，用实验标准差 S 替代真值σ。Z 值取 2，则概率 P（Z≤2）= φ（2）= 0.975。

那么 P（-2≤Z≤2）=φ（2）- φ（-2）= 2φ（2）-1 = 0.95，表示落在区间 μ ± 2 s 范围内的概率为95%。因此，对于近似正态分布，95% 的概率水平下，Z = 2，因此= 2.83。对于一般的统计使用，将 √2 Z修约为 2.8。

在对重复性或再现性条件下得到的 2 个单一测试或测量结果进行检验时，应与重复性限 r = 2.8 σr或再现性限 R = 2.8 σR进行比较。也就是说，在精密度试验中得到的 2 个测试或测量结果（这 2 个结果可能是多个结果平均值或中位数）的差值与 r = 2.8 σr或 R = 2.8 σR进行比较，≤ r 或 R，则表示这 2 个测试或测量结果是可接受的。GB/T 3358.5—2009《统计学词及词汇及符号 第 2 部分：应用统计》指出：“在规定实验方法的国家标准或类似技术文件中，按规定的试验条件，当明确指出两次测量结果之差的重复性限 r 或复现性限 R 时，如无特殊说明，则测量结果标准不确定度为 u (Xi) = r/2. 83 或 u (Xi) = R/2. 83。”这就是说，在制定标准分析方法时，给出该方法的重复性限或复现性限。在翻斗式雨量传感器检测中，重复性限取 r = 2.83 Sr。

由 GB/T 6379.1—2004 可知重复性限和再现性限是通过实验室间比对试验的测试或测量结果确定的。对于标准中的重复性限和再现性限也是标准起草单位组织多个实验室进行比对试验确定的。所以，一般情况不需要深入了解标准中重复性限和再现性限是怎么得来的，只需要利用它验证标准方法及其他证明实验室有能力控制精密度的证据。

4 翻斗式雨量传感器重复性评定方法

4.1 重复性标准差计算

要计算翻斗计量误差重复性限 r，先要计算翻斗计量误差的重复性标准差，翻斗计量误差的重复性标准差是以实验标准差表示的，并按贝塞尔公式计算翻斗计量误差的实验标准差 Sr。

例如，检测某一翻斗式雨量传感器，分别按大、中、小降雨强度对其进行重复性试验。根据 GB/ T 21978.2—2014 《降水量观测仪器第二部分：翻斗式雨量传感器》对仪器重复性试验要求，翻斗计量误差进行 6 次试验，其结果（6 个计量误差的绝对值）及计算出的重复性标准差（实验标准差）Sr如表 2 所示。

表 2 翻斗式雨量传感器重复性试验结果表

4.2 重复性限计算

根据 GB/T 21978.2—2014 中重复性要求，按r = 2.83 Sr，分别计算大、中、小降雨强度下的翻斗误差重复性限 r，各重复性限如下：r大= 2.83 Sr= 2.83×0.31 = 0.88；r中= 2.83 Sr= 2.83×0.21 = 0.59；r小= 2.83 Sr= 2.83×0.25 = 0.71。

可以看出在重复性条件下的试验，大、中、小降雨强度下的翻斗误差重复性限均小于 1%，由此可证明被检翻斗式雨量传感器重复性符合要求。

5 结语

作为翻斗式雨量传感器精度检测中的最重要的部分，本研究针对翻斗式雨量传感器精密度检测试验中重复性试验数据，利用统计学的方法，理论结合实际测试实验数据，确定重复性评定中的有关数据的统计处理和计算方法。为在实际工作中的翻斗式雨量传感器精度检测中重复性限的计算提供了具体的计算公式，为翻斗式雨量传感器精度检测工作更上一个台阶打下了坚实的基础。

[1] 中华人民共和国水利部. 降水量观测仪器 第 2 部分：翻斗式雨量传感器：GB/T 21978.2—2014 [S]. 北京：中国标准出版社，2014.

[2] 国家质量监督检验检疫总局. 通用计量术语及定义：JJF 1001—2011 [S]. 北京：中国质检出版社，2011: 16.

[3] 全国统计方法应用标准化技术委员会. 统计学词汇及符号 第 2 部分：应用统计：GB/T 3358.2—2009[S]. 北京：中国标准出版社，2009: 25.

[4] 国家质量监督检验检疫总局. 测量仪器特性评定：JJF 1094—2002[S]. 北京：中国计量出版社，2002: 6.

[5] 李德辉. 校准实验室能力验证中测量仪器的重复性和稳定性[J]. 中国计量，2009 (4): 41-42.

[6] 国家质量监督检验检疫总局. 测量不确定度评定与表示：JJF 1059.1—2012[S].北京：中国标准出版社，2012: 4.

[7] 中国标准化研究院. 测量方法与结果的准确度（正确度与精密度）第 1 部分：总则与定义：GB/T 6379.1—2004 [S]. 北京：中国标准出版社，2004: 3.

[8] 王承忠，朱海根. 实验室质量体系运行中的技术难点及解决方法——方法确认、人员或方法比对的判定 [J]. 物理测试，2011（增刊 1）: 87-89.

Statistical processing method for repetitive test of tipping bucket rain gauge

DENG Chao, XU Haifeng, SU Nan, LIN Wei
(Hydrological Instruments and Geotechnical Instrumentation for Quality Supervision and Testing Center, the Ministry of Water Resources, Nanjing 210012, China)

The repeatability of a measuring instrument is the major indexes re fl ecting the precision of the measuring instrument. Repeatability test is one of the most important steps in the performance detection of the tipping bucket rain gauge. The processing of test data is also the most complicated in the whole test. In this paper, the statistical processing and calculation method of the repetitive experimental data in the precision test of the tipping bucket rain gauge, and a detailed calculation formula for the calculation of the repetitive limit in the precision detection of the tipping bucket rain gauge are provided. And the method of assessing the repetitive test data of the tipping bucket rain gauge is described in detail. The results show that the precision detection of the bucket type rainfall sensor is in accordance with the standard, and is also feasible to lay the foundation for improving the precision of the tipping bucket rain gauge.

tipping bucket rain gauge; repeatability; repetitive standard deviation; repeatability limit

P335

A

1674-9405(2017)04-0058-03

10.19364/j.1674-9405.2017.04.011

2017-05-17

邓 超（1983-），男，安徽合肥人，工程师，主要研究方向为水文仪器及土壤墒情。