“泛在智能”时代热力学与统计物理教学设计实践——以卡诺循环教学设计为例

塔金星

(东北林业大学理学院，哈尔滨 150040)

在热力学与统计物理的卡诺循环教学中，理想气体的卡诺循环是重点教学内容。在分析过程中，会利用到很多公式，能够考察学生对功的公式的理解程度。等温过程中需要利用到物态方程，绝热过程中涉及焦耳定律、泊松方程、绝热方程的合理运用，这两个过程还都要用到数学中的微积分公式。

随着“泛在智能”时代的到来，越来越多的教师已经完全采用了课件等多媒体形式进行授课，优点显而易见，包含丰富多彩的图片、音频、视频，在听觉和视觉等方面可以强烈刺激学生的感官，引起学生共鸣。但对学生的思维引导有所欠缺，除了利用课件授课以外，传统板书教学依然很有必要。

1 多媒体课件内容设计

教学从基本概念讲起，然后过渡到理论公式的推导及其意义分析。当基本概念和图示较多时，不适合传统板书教学。为提高课堂教学效率，该部分采用课件形式进行授课，具体设计如下：

①循环：经历一系列变化后又回到初始状态的整个过程。

②表示法：P-V图中的封闭曲线，如图1、图2所示。

③分类：正循环(系统对外做功)、逆循环(外界对系统做功)。

④代表：卡诺循环、斯特林循环，如图1、图2 所示。

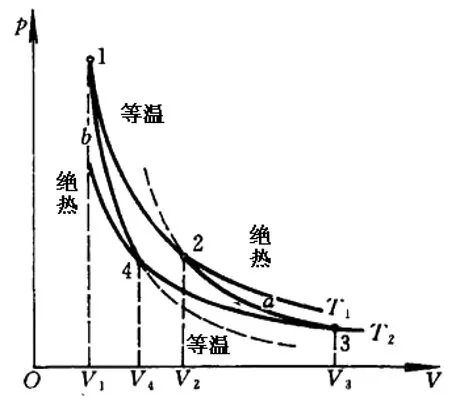
图1 卡诺循环

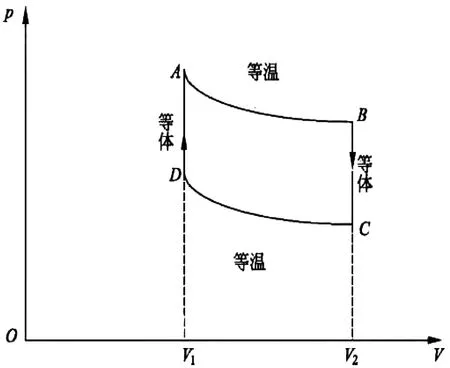
图2 斯特林循环

卡诺循环由两个准静态的等温过程与两个准静态的绝热过程构成。斯特林循环由两个准静态的等温过程与两个准静态的等体过程构成。在这部分课堂教学中，只分析卡诺循环，学生学会了分析方法后，要求学生课后独立分析斯特林循环，巩固所学内容。还可以添加热机介绍视频，使学生更直观地了解热机工作情况。

2 传统板书内容设计

以1 mol理想气体为研究对象，分别分析卡诺循环中等温过程与绝热过程的做功和传热。

2.1 等温过程

利用物态方程、准静态做功微分式、热力学第一定律微分式联立可得：

(1)

讨论：当体积膨胀时，做功为负，系统吸收热量保持等温。当体积压缩时，做功为正，系统放热保持等温。这一部分难度不大，学生能够理解。

2.2 绝热过程

思维引导主要体现在定律及公式的合理运用，需要利用作功公式、泊松方程、绝热指数与等容热容关系、积分技巧。

方法一：由绝热方程pVγ=C变形可得：

(2)

利用积分技巧、绝热方程、绝热指数与等容热容关系可得：

(3)

在得出具体结果前，为启发学生思考，提出了引导性问题：

①在计算功时，为什么用泊松方程中的形式去表示压强P？而不用物态方程？

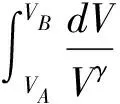
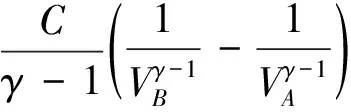
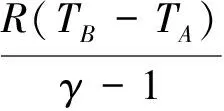
⑤结果CV(TB-TA)有具体的物理意义吗？进而引出更简洁的计算方法二。

方法二：绝热过程无热量交换，根据热力学第一定律及焦耳定律可得：

(4)

积分结果与式(3)相同。该方法不需要复杂的数学积分及泊松方程等难点知识，计算过程简洁明了，更能体现物理思维过程。

3 结语

“泛在智能”时代可以为教师教学提供丰富多彩的课程背景资料和良好的授课环境。但热力学与统计物理课程理论性较强，公式繁多，除了借助现代化技术手段的多媒体课件以外，传统的板书教学仍然是很主要的教学形式。针对具体的教学内容和学生的接受程度，多媒体课件和板书教学的应用比例需不断调整，不能完全依赖多媒体。