自适应PID控制算法在智能车控制系统的应用

盛柳青

(1.安徽汽车职业技术学院,合肥230601;2.安徽汽车工业技师学院机电工程系,合肥230601)

伴随着当今社会科学技术日新月异的更新发展,智能控制广泛应用到各行各业中。其中以智能控制为基础,智能汽车前景广阔且发展迅速。智能车系统是智能汽车的缩小版,但二者在控制系统构成和控制信息处理方面有不少相似之处,也就是说智能车系统是智能汽车良好的实验平台[1]。高效的软件程序是智能车高速平稳自动寻线的基础,而对智能车转向和速度的控制则是智能车的重要和核心环节[2]。

PID控制是工业控制的主要技术之一,它结构简单、稳定性好、工作可靠、调整方便。PID控制一般适用于两种情况:一是我们对研究中的系统或被控对象完全不了解;二是测量系统参数时没有有效的手段。其中,位置式PID算法的输出是控制量的全量输出,要用到过去偏差的累加值,容易产生大的累加误差;增量型算法中对增量的确定仅由最近几次偏差采样值得出而不需要进行累加,因此在控制量的计算中计算精度的影响较小[3]。但传统的PID算法在环境变化时无法实现自整定参数调整和动态,参数调整导致小车的行驶易受干扰而振荡,影响小车的稳定行驶。肖建文和李永科运用增量型PID控制算法来控制舵机和电机,但应用于变化的环境中时,该算法在进行控制参数自整定时无法实时化,因此小车在整个运行过程中容易受到干扰而导致振荡[4]。为了解决这个问题,杨惠等主张应用模糊PID算法,该方法主要针对PID参数无法实现自整定的问题,但模糊控制的规则主要由研究者自身的先验知识和实践经验决定的,这就使其具有不完整、主观性强等缺点[5]。郑飞等提出的分段式PID控制,采用不同路段上不同速度匹配不同的PID参数值的方法,从而实现分段控制的效果,这种算法很大程度上提高了控制精度,但是仍然无法解决PID过程中系统振荡和敏感性大等问题[6]。为此,本文提出一种改进的单神经元自适应PID控制算法,通过实验比对,该控制系统在自学习、系统响应、鲁棒性等方面得到显著改善,经过验证可以实现智能小车的稳定控制。

一、智能车控制理论与算法

智能车的整个设计是通过CCD检测获得的路径信息来对智能车进行控制,即对小车的行驶速度和转向进行控制。优良的控制才能提高小车的平均速度,增加小车的稳定性,因此必须对智能车的行驶速度和行驶方向进行算法控制研究。在智能车控制算法中常采用的算法有PID控制器、模糊控制器、最优控制器等。其中传统的控制方法是PID控制器和最优控制器。

智能车可以看作一个位置随动系统,跑道的变化会对智能车控制系统的稳定性产生扰动,如果将这个系统视为恒值控制系统,要求智能车必须平稳快速运行以适应路径变化。因此好车更要有好的控制算法,既满足赛道路径的多变性,又满足智能车控制系统的稳定性。

运行中,智能车行驶环境受各处赛道摩擦力不一样、光照等因素的影响。若舵机控制出错,智能汽车极有可能出界犯规,因此对电机和舵机的控制必须实时准确跟踪变化的赛道路径。

(一)PID控制理论

PID调节器是对偏差的比例(P)、积分(I)和微分(D)进行控制的。它在连续系统中是技术成熟、应用广泛的一种调节器,具有结构简单、参数容易调整等优点,而且在算法上容易实现,鲁棒性好,控制精度高。

传统PID控制系统的主要环节包括PID控制器、控制对象。该控制器进行线性运算,先计算出偏差(由给定值r(t)与输出值y(t)得出),再将获得的偏差进行P(比例)、I(积分)、D(微分)处理并进行线性组合得出控制量,从而实现控制被控对象的目的。

(二)位置型PID控制算法

采样控制过程是计算机控制的本质,它的控制量计算是通过采样时刻的偏差,所以不能运用连续PID控制算法进行直接计算,而需要进行离散化。必须将连续时间t用一系列的采样时刻kt代替,积分用和式代替,微分用增量代替,则可得数字PID位置型控制算式为:

(三)增量型PID算法

位置型控制算法需要累加偏差e(i),不但需要较多的存储单元,同时编写程序也较复杂。增量型控制指的是数字控制器的输出是增量Δu(k)。当执行机构需要的不是控制量的绝对量而是增量(如驱动步进电机),这时应运用增量型PID控制。

传统PID控制算法是将行驶方向和道路中心线的距离偏差输入PID控制器的I环节和D环节,得出积分值、微分值,再按照线性规律组合计算出的数值和偏差,实际的输出由比例(P)环节得出。而CCD传感器中得到的道路信息是离散的,所以必须采用离散化的增量型PID算法[7]。

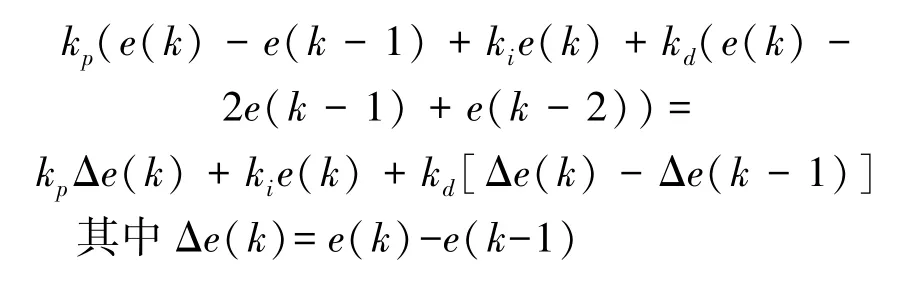
二、基于单神经元网络的PID智能控制

通过实时地调节P、I、D三个控制参数,可以提高PID控制的精度和稳定性,使控制系统依据误差可以实时地做出相应的响应。神经网络具有“非线性”特性,可以通过自我学习和自我整定来获得最合适的P、I、D控制参数,可以进行精确的控制。

单神经元自适应智能PID控制器的基本构成是单神经元,其具有结构简单、对变化的环境适应性强、鲁棒性好等优点。

(一)单神经元自适应PID控制

王宁等深入研究了单神经元控制问题[8],提出了一种单神经元自适应PID控制结构,如图1所示。

图1 单神经元自适应PID控制

(二)调节单神经元PID控制器参数

调节学习速率ηP、ηI、ηD,可先将其设定为最小值。如果调节过程中从超调状态过渡到平稳状态所需的时间过长,可以通过增加ηP和ηD来缩短过渡时间;反之则减小。但如果调节环节中超调过大、上升时间过短,则应减小ηP来延长过渡时间;反之增大。

单神经元自适应控制器具有自适应、自组织功能,这个功能的实现是通过对加权系数的调整,而权系数的调整是通过有监督的Hebb学习规则来实现的[9]。

(三)有监督的Hebb学习规则

有监督的Hebb学习规则是一种将无监督的Hebb学习规则与有监督的Delta学习规则结合起来的一种学习算法:Δwij(k)=η(dj(k)-οj(k))×οj(k)οi(k)。

其中,wij表示神经元i和神经元j的联接权值;οi表示神经元i的激活值;οj表示神经元j的激活值;dj表示希望的输出。

(四)改进的单神经元自适应PID控制算法及学习算法

取n=3,则单神经元自适应PID控制系统的状态输入:t时刻、t-1时刻、t-2时刻小车的行驶方向与道路中心线之间的距离偏差如下:

故wi(k)可以看作是增量式PID的比例、积分、微分系数,ηP、ηI、ηD分别是比例、积分、微分的学习速率;K是神经元的比例系数;z(k)=e(k)。积分I、比例P、微分D调整不同的权系数应采用不同的学习速率ηI、ηP、ηD来实现。 选择合适的K值显得尤为重要。K值取得越大,则调节越快,但严重的超调现象突显,甚至导致控制系统的不稳定。当被控对象时延过大时,K值则必须进行减少,以保证系统的稳定。K值取得太小,会导致系统变得过慢。

针对单神经元自适应控制提出过很多种改进方法[10]。在实际应用中,大量的实践证明,PID参数的在线学习修正关键由e(k)和Δe(k)决定。故将单神经元自适应PID控制算法中的加权系数学习修正部分进行必要的调节,即将其中的xi(k)改为e(k)+θΔe(k),改进后的算法表达如下:

三、仿真及结果分析

被控对象的简易数学模型为:

输入指令取某一方波信号:yd(k)=0.5sgn(sin(4πt)),采样时间为1ms,θ=1,同时采用四种学习规则进行单神经元PID控制,即改进的Hebb学习规则、无监督的Hebb学习规则、有监督的Delta学习规则和有监督的Hebb学习规则。使用Matlab软件仿真后结果,如图2所示。

图2 Matlab软件仿真结果对比图

单神经元自适应智能PID控制器由神经元构 成,神经元具有自学习能力、自适应能力,故此控制器具有简单的结构、较强的环境适应能力,同时鲁棒性较强。由仿真图可得,相较于其他学习规则,改进的单神经元自适应PID控制器有更强的抗干扰性和更好的稳定性。由图可知,PID三个参数稳定时间和超调量都较小,由此可以得出,该控制器提高了系统鲁棒性和快速响应性。

四、结语

神经网络(Neural Network)是模拟人脑思维方式的数学模型。20世纪80年代末期发展起来的神经网络控制属于自动控制领域的前沿学科之一。它属于智能控制中的一个重要分支,在解决复杂系统(非线性、不确定、不确知)的控制问题中提出了新思路。神经网络算法可以通过自我学习自适应调整P、I、D参数,用于智能车这种非线性、时变系统特别适合,具备比较好的稳定性和适应性。在有监督的Hebb学习规则基础上通过修改单神经元自适应PID控制算法中的加权系数学习修正部分,进一步提高了控制效果。通过实验结果的对比,改进的控制算法进一步提高了控制的精度、快速响应性和鲁棒性。