基于改进粒子群优化算法的综合能源系统多目标优化

徐建军，赵书琪，马睿，张博，潘力超，孙瑜

(东北石油大学 电气信息工程学院，黑龙江 大庆 163318)

由于化石燃料具有不可再生性，提高能源利用率、分布式能源的规模性开发、能量大规模储存等问题已成为科学家们研究的焦点[1-4]。英国等欧洲国家最早对综合能源系统(integrated energy system，IES)展开了研究，涉及多种能源间的协同、分布式能源并网、能源与基础设施以及交通系统等诸多方面[5-6]。IES按其规模可分为跨区域级、区域级和园区级，通过能量耦合组件、能量集线器、能量路由器，统筹管理、协同规划冷、热、电、气等不同类型能源在生产、转换、销售等环节，实现能量梯度利用，可有效提高能源利用率[7-12]。随着能源改革理念的提出，区域综合能源系统(regional integrated energy system，RIES)已成为我国能源领域的重要研究方向，其具有节能、高效、环保等显著优势[11]。

目前我国已有不少学者对RIES的优化问题进行了研究。文献[13-15]针对分布式能源消纳、储能设备并网等问题进行研究：文献[13]在系统中增设电转气装置消纳风能，减低系统的弃风水平，评估经济效益；文献[14]侧重对新能源可靠性的研究，建立滚动模型和动态调整模型，验证了小时间尺度模型适应负荷变化的优越性；文献[15]针对光伏电池的不确定性问题，采用区间线性规划，给出最优解区间。

在优化模型方面，文献[16-18]以经济最优为目标：文献[16]验证多目标RIES模型可有效减小燃气轮机容量配置，显著降低运行成本；文献[17]采用混合潮流计算方法比较系统不同运行模式下的经济性；文献[18]建立效率最高、费用最低和排放3个优化模型，考虑不同分时电价策略下的最优运行方式。文献[19]针对沼气冷热电联供系统，以经济和环境效益为综合优化目标，对系统进行优化。文献[20-21]建立了IES动态优化模型：文献[20]提出两阶段多尺度滚动优化策略，实现对设备运行状态的实时调整；文献[21]建立IES规划、优化的两阶段模型，验证了其可行性。

在优化算法方面，IES优化问题的求解方法主要有线性规划、非线性规划、混合整数规划等，求解器主要有MATLAB的Cplex工具箱、人工智能算法﹝粒子群优化(particle swarm optimization，PSO)算法、遗传算法、退火算法等﹞和LINGO商业软件等。文献[22]基于快速PSO算法，提出智能家庭能源优化控制策略，并与遗传算法优化结果对比；文献[23]基于混合线性规划的方法，使用Yalmip工具箱和Cplex工具箱对某省的RIES进行仿真分析；文献[24]基于最小二乘法，建立数据的历史回归模型，提出了潮流线性化方法；文献[25]基于内点法，提出电热耦合系统的最优能流处理方法；文献[26]采用贪婪-变邻域蛛网算法，计算全局最优解，有效提高了计算效率；文献[27]提出改进遗传算法和非支配排序算法，采用密度估计和拥挤比较算子代替共享参数运算，降低了计算的复杂度；文献[28]对集中式算法、广义Benders分解算法以及交替方向乘子法进行概述，通过算例比较三者的计算速度和精度。

综上所述，目前对RIES优化的研究主要集中在分布式能源、储能设备并网和多目标优化等方面，人工智能算法成为国内外学者处理优化问题的重要途径，但随着模型复杂化，最优解维度增多，传统的人工智能算法存在收敛性差、容易陷入局部最优解的问题。基于此，本文使用非线性权重策略对PSO算法进行改进，引入粒子浓度评价算子；建立RIES数学模型，以经济性、高效性和环保性为优化目标，通过隶属度函数和层次分析法将多目标转化为单目标，并通过此模型对算法进行检验。

1 RIES建模

1.1 RIES结构

RIES通过电力网、热力网、天然气网、输冷网[7]将系统中各个独立设备耦合起来，其能量流结构如图1所示，燃气轮机发电过程中，天然气的化学能未完全转化为电能，所产生的余热超过70%被余热锅炉回收进入热力管网，同时电锅炉、电制冷机、吸收式制冷机等设备统筹规划运行，实现能量梯度利用，大大提高了能源利用率和经济效益[29]。

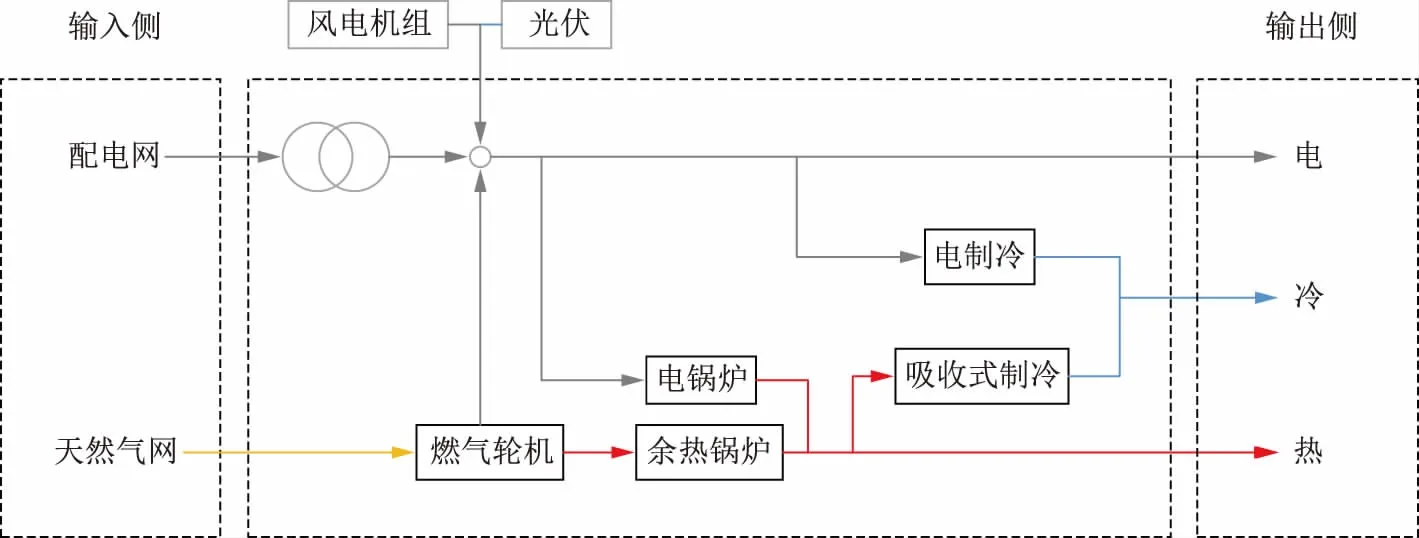
图1 RIES能量流结构Fig.1 RIES energy flow structure

1.2 典型设备建模

本文建立的RIES模型包括燃气轮机(gas turbine, GT)、吸收式制冷机(absorption chiller, AC)、余热锅炉(waste heat boiler, WHB)、电制冷机(electric chiller, EC)、电锅炉(electric boiler, EB)等能量转换设备，风电机组(wind turbine, WT)、光伏电源(photovoltaic, PV)等分布式能源，以及储电设备(energy storage, ES)、储热设备(heat storage, HS)等储能系统(energy storage system, ESS)。

a)由燃气轮机和余热锅炉构成的热电联供装置的数学模型为：

(1)

QWHB=ηrecQGT，

(2)

(3)

式(1)—(3)中：QGT为燃气轮机总产热功率(kW)；QWHB为余热锅炉的热回收功率(kW)；PGT为燃气轮机的输出电功率(kW)；VGT为天然气消耗量(m3)；LNG为天然气低位热值(kWh/m3)，取9.78 kWh/m3；ηe为燃气轮机发电效率；ηrec为燃气轮机的回热系数；ηL为热损失系数；h为设备运行时间(h)。

b)电锅炉模型为

QEB=ηEBPEB.

(4)

式中：PEB、QEB分别为电锅炉的输入功率(kW)和输出功率(kW)；ηEB为电锅炉的电热转换效率。

c)吸收式制冷机和电制冷机模型为：

CAC=QACcAC，

(5)

CEC=PECcEC.

(6)

式(5)—(6)中：CAC、CEC分别为吸收式制冷机、电制冷机的制冷功率(kW)；QAC、PEC分别为制冷所需要的热功率(kW)和电功率(kW)；cAC、cEC分别为吸收式制冷机、电制冷机的制冷系数。

d)光伏发电的输出功率模型为：

(7)

{θC}℃={θamd}℃+30{G}kW/m2.

(8)

式(7)—(8)中：PSTC为标准情况下的测试功率(kW)；PPV为光伏电池的输出功率(kW)；GAC为光照强度(W/m2)；GSTC为测试条件光照强度(W/m2)；K为功率温度系数，取-0.004 7；G为太阳辐射值(kW/m2)；θC为电池温度(℃)；θamd为外界环境温度(℃)；θr为参考温度(℃)，取25 ℃。

e)风能发电的输出功率模型为

(9)

式中：PWT为风力机组输出功率(kW)；r为叶片半径(m)；ρ为空气密度(kg/m3)；cp为风力机的风能利用系数；v为空气流速(m/s)。

f)储能设备充放电是动态平衡过程，有储能、放能、停运3个状态，储能量与多个因素有关，其数学模型为：

(10)

(11)

式(10)—(11)中：将1 d分为24个时段，每个时段长度Δt=1 h，t表示当前时段，t+1表示下一时段；EES(t)为储电设备的储电量(kWh)；PES,c(t)、PES,d(t)为储电设备充电、放电功率(kW)；ηES,c、ηES,d为储电设备充电、放电效率；EHS(t)为储热设备的储热量(kWh)；PHS,c(t)、PHS,d(t)为储热设备储热、放热功率(kW)；ηHS,c、ηHS,d为储热设备储热、放热效率。

1.3 优化目标

a)经济性由系统日收益表示，目标函数

F1=Wsell-(Wgas+WHS+WES+WE)，

(12)

(13)

(14)

(15)

(16)

式(12)—(16)中：Wsell为售电热冷的营业额；Wq、Wc为日供热和供冷费用；Wgas、WE、WES、WHS为天然气费用、购电费用、储电设备运行费用、储热设备运行费用；Lp(t)为用户消耗的电负荷功率(kW)；be为电网实时电价；bgrid为储热价格，一般由水泵耗电产生；b为储电设备单价；M为储电设备使用次数；CES为储电设备容量；PE(t)为电网购电功率。

b)环保性由CO2排放量表示，目标函数

(17)

式中：cgas为燃气轮机燃烧天然气对应的CO2排放系数，取220 g/kWh；cgird为电网购电对应的CO2排放系数，取877 g/kMh。

c)高效性由能源利用率表示，目标函数

(18)

Pout(t)=Lp(t)+Lq(t)+Lc(t)，

(19)

(20)

式(18)—(20)中：Pin、Pout分别为RIES的输出功率(kW)和输入功率(kW)；Lq(t)、Lc(t)分别为用户消耗的热、冷负荷功率(kW)；Pgrid为电网购电功率(kW)；ηgrid为我国电网发电平均效率。

1.4 约束条件

RIES中冷热电负荷平衡条件及设备负荷约束关系为：

PGT(t)+PPV(t)+PWT(t)+Pgrid(t)+PES,d(t)=

PES,c(t)+PEB(t)+PEC(t)+Lp(t).

(21)

QWHB(t)+QEB(t)+QHS,d(t)=

QAC(t)+QHS,c(t)+Lq(t).

(22)

CAC(t)+CEC(t)=Lc(t).

(23)

系统中典型设备应考虑式(1)—(11)所示的出力关系约束，还需考虑式(24)所示的出力上下限约束及式(25)所示的稳定性约束：

(24)

(25)

式(24)—(25)中：Pi、Qi为设备i的电功率、热功率(kW)；Pi.max、Pi.min分别为设备i的最大电功率、最小电功率(kW)；Qi.max、Qi.min为设备i的最大热功率、最小热功率(kW)；rGT为燃气轮机的最大爬坡速率。

2 优化算法

2.1 多目标处理

2.1.1 隶属度函数

本文通过隶属度函数将目标函数分别进行归一化、线性叠加，从而将多目标转化为单目标，再借助单目标优化算法求解多目标函数最优解。

隶属度函数模型尚未明确定义，由使用者根据数学模型自行设定，经济性、高效性指标的隶属度函数模型如式(26)所示，环保性指标的隶属度函数模型如式(27)所示：

(26)

(27)

式(26)—(27)中：Ai为目标函数的隶属度，其中A1为偏大型，A2为偏小型；fi为第i个指标的目标函数；fi.min、fi.max为第i个目标的隶属度函数临界点，视Fi的范围而定。

2.1.2 层次分析法

由于经济性、环保性和高效性指标之间关系较为复杂，选择决策系数时，容易因为主观性过强导致优化调度结果不合理，故本文使用层次分析法确定隶属度函数的权重系数[30]。决策分析法是在深入分析各个复杂决策问题的影响因素基础上，使决策的思维过程数学化，从而为多目标问题提供较为合理的决策方法。具体步骤如下：

a)将各个指标的重要程度用1—9的整数aij表示；

b)两两比较指标的重要性，形成判别矩阵

(28)

式中：D为判别矩阵；ai、aj表示第i、j个指标的重要性程度。

c)求解判别矩阵的特征值与特征向量，并进行如式(29)所示的一致性校验，满足条件后，将最大特征值对应的特征矩阵进行标准化，得到权重系数。

(29)

式中：λmax为矩阵最大特征根；βRI为平均随机一致性指标，与判别矩阵维度n有关；βCI为一致性指标；βCR为一致性比例，一般认为其小于0.1时矩阵满足一致性检验。

由于本文选择的高效性指标为能源利用率，与经济性有交叉，故得到指标权重后，对高效性和经济性指标引入重合系数，再对3个指标进行标准化，本文的重合系数取0.65。最后，得到综合目标

F=ε1A1(f1)+ε2A2(f2)+ε3A3(f3).

(30)

式中εi为各目标的权重系数。

2.2 PSO算法改进

2.2.1 非线性权重系数

PSO算法将在空间中寻找最优解的过程类比成鸟类觅食的过程，粒子每一轮搜捕结束后，粒子按照特定规律向已有的最优解移动，同时个体最优解不断更新，从而完成最优解的求解过程。

传统PSO算法中，权重系数为常数或线性变化，本文使用如式(31)所示的非线性惯性权重w[31]，可以使粒子在搜捕初期保持较大惯性，有利于全局搜索，后期缓慢靠近最优解，避免求解轨迹在最优解附近振荡，从而提高PSO算法的全局搜索能力，避免陷入全局最优解，并提高收敛速度。

(31)

式中：k为控制因子，影响惯性权重变化趋势，本文取k=5；wstart、wend为迭代起始和终止时的惯性权重，通常取1和0；g为本轮迭代次数；gm为最大迭代次数。

2.2.2 粒子浓度评价算子

免疫算法中，抗体浓度过高代表可行解在某一区域内集中，算法容易陷入局部最优解；抗体浓度评价算子能识别相似度较高的可行解，并适当对其进行抑制，从而提高可行解的多样性，避免陷入局部最优解。

类比抗体浓度评价算子，引入如式(32)所示的粒子浓度评价算子，协同考虑亲和度函数与适应度函数，从而提高粒子多样性，避免陷入局部最优解。

(32)

(33)

式(32)—(33)中：pi、pj为粒子i、j的位置，i，j=1，2，…，N，N为粒子总数；d(i)为粒子i的亲密度；S(i,j)表示粒子i和j是否密集，1为密集，0为不密集；δs为将2个粒子视为密集的最大距离。

单次迭代的流程如图2所示。在求得粒子适应度函数后，计算粒子亲密度函数，将适应度函数的结果减去该粒子的亲密度，作为新的适应度，对粒子进行排序，从而得到本次迭代中考虑亲密度情况下的最优解，更新粒子，进入下一次迭代。粒子浓度算子相当于给PSO算法引入1个浓度罚函数，降低粒子向浓度过大的方向运动的速度。

图2 单次迭代流程Fig.2 Single iteration flow chart

迭代50次后，粒子基本聚集在最优解附近，亲密度函数的引入不利于粒子精确地寻找最优解，因此在计算新的适应度时，采用如式(34)所示的线性递减权重，得到新的粒子适应度如式(35)所示：

(34)

Hden.i(x)=Hi(x)-ρ(x)d(i).

(35)

式(34)—(35)中：x为本轮迭代次数；xm为迭代总数；ρ(x)为第x次迭代时的亲密度函数权重；Hi为第i个粒子的适应度；Hden.i为考虑粒子浓度后的第i个粒子的适应度。

2.3 PSO算法与fmincon嵌套

fmincon函数为MATLAB中自带的非线性规划函数，可求解非线性问题的最优解。本文基于MATLAB R2019a，设置fmincon函数的目标函数和约束条件，使得每输入1组储能设备出力矩阵，即可得到此储能设备运行方式下的最优解。将此非线性优化作为PSO算法的适应度函数，以储能设备出力作为自变量，求解储能设备的最佳运行方式。最后，将储能设备最佳出力代入fmincon函数，求解其他设备最佳出力方式和系统综合指标。程序流程如图3所示。

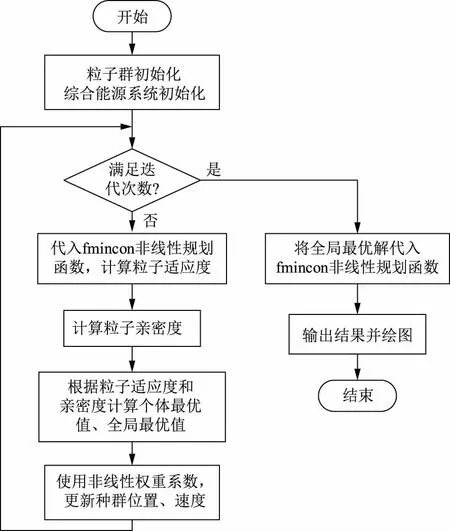
图3 改进PSO算法流程Fig.3 Improved PSO flowchart

3 算例仿真

3.1 算例参数

本文选取的典型RIES设备组成如下：1台最大功率5 MW的燃气轮机，1台最大功率3 MW的余热锅炉，5台最大功率600 kW的电锅炉，4台最大功率200 kW的电制冷机，4台最大功率200 kW的吸收式制冷机，1台最大出力500 kW的风电机组和1台最大出力300 kW的太阳能电池组，3台最大容量500 kWh的蓄电池和3台最大容量500 kWh的蓄热设备。相同设备之间均匀出力，与电网并网运行，可以从电网购电，但不可以向电网售电。算例参数如图4所示。

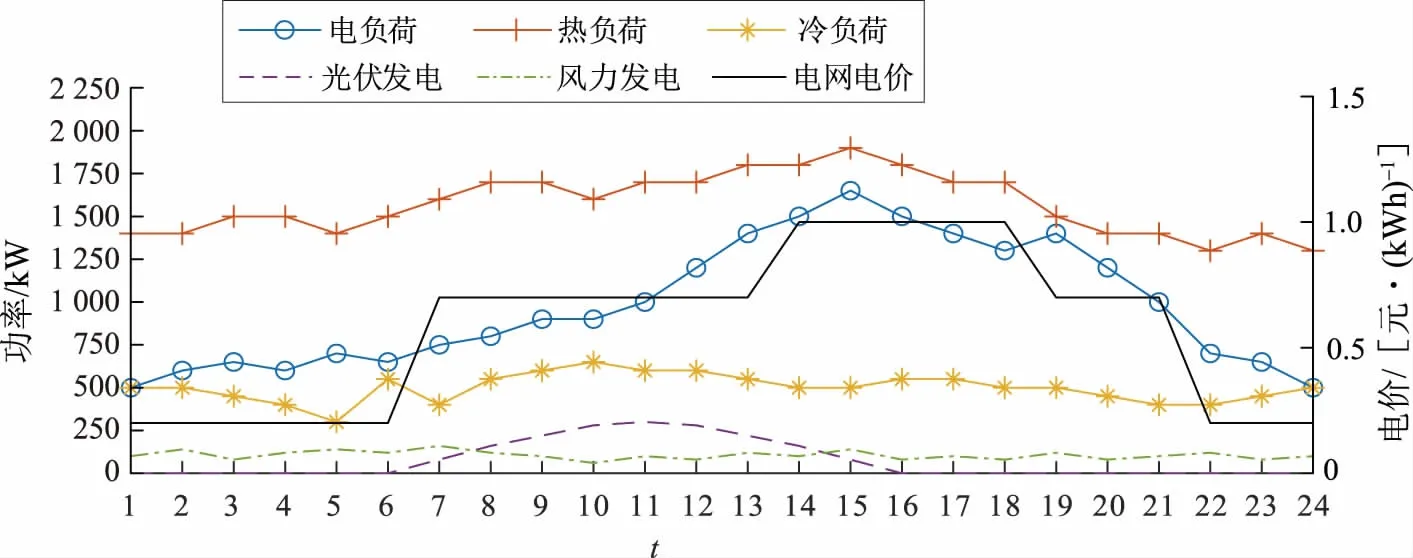
图4 算例参数Fig.4 Calculation parameters

3.2 算法优化结果

求解上述算例时，改进前后PSO算法的适应度曲线如图5所示，收敛速度可由达到最佳适应度时的迭代次数体现，全局适应性由最佳适应度体现。改进后，迭代300次后的适应度明显高于改进前，且依然保持较好的收敛性，迭代75次时接近最优解，故该改进PSO算法具有良好的收敛性和全局适应性。

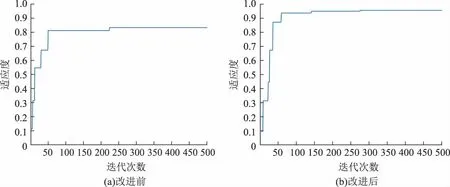
图5 PSO算法适应度Fig.5 Fitness of PSO algorithm

3.3 系统设备出力情况

系统各个设备出力情况如图6所示。

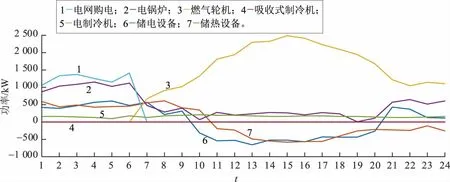
图6 设备出力情况Fig.6 Equipment output

a)储能设备运行情况：09：00—20：00，储电设备处于充电状态；21：00—次日09：00，储电设备处于放电状态；01：00—10：00，储热设备处于放热状态；11：00—24：00，储热设备处于吸热状态。

b)电负荷供应：01：00—06：00，系统从电网购电；07：00—24：00，燃气轮机出力提供电能。

c)热负荷供应：01：00—09：00，电锅炉出力较多；07：00—21：00，热量主要由余热锅炉吸收的燃气轮机余热供应。

3.4 优化结果对比

将RIES模型分别进行经济性、环保性和高效性单目标优化，运行结果与多目标优化进行对比，结果见表1。以经济性为优化目标时，CO2排放量和能源利用率2项指标较多目标优化时有明显差距，满意度最低，说明经济性最佳将以环保性和高效性差为代价。同时，环保性和节能性指标的CO2排放量和能源利用率指标均较好，但日收益明显降低。多目标优化综合考虑经济、环保、高效等因素，满意度为0.961，明显高于单目标优化，说明多目标优化方案能满足消费者及供电公司的多维度需求。

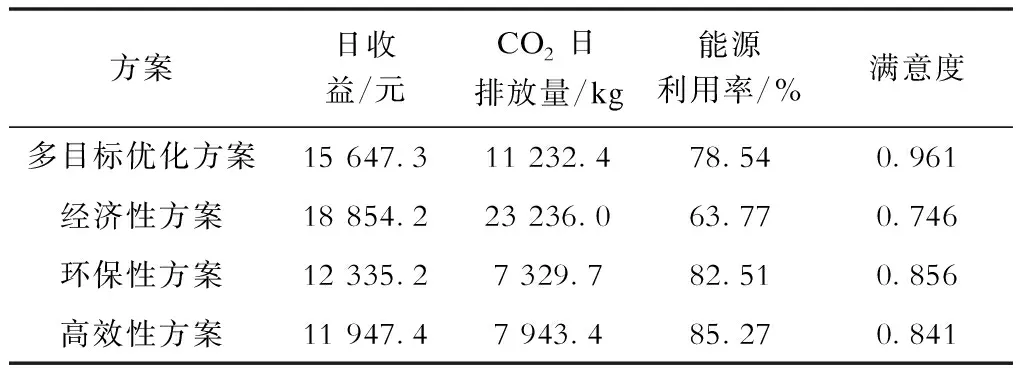
表1 优化结果对比Tab.1 Multi-objective optimization results

4 结束语

本文对传统PSO算法进行改进，使用非线性权重系数，引入粒子浓度评价算子，提出了针对维数较多的PSO算法的改进方法。通过RIES多目标优化算例对算法改进效果进行验证，结果表明该算法可增强粒子的全局搜索能力，对于维数较大的算例，可有效提高算法全局适应性，且收敛速度依然保持较高水平。此外，算例结果表明，仅考虑单一目标的IES优化满意度较差，通过层次分析法合理调节系统经济性、环保性和高效性指标的重要性权重，有利于提高系统的综合性能。