基于高斯模型的海上风电场尾流效应评估及偏航优化

刘奕元，辛妍丽，唐文虎，Salvy Bourguet

(1.华南理工大学 电力学院， 广东 广州 510641；2.南特大学南特大西洋能源电力研究所, 法国卢瓦尔河大区 圣纳泽尔 44602)

我国海上风电近年来展现出蓬勃发展趋势，但尾流效应导致的风电场出力下降问题不可忽视。为获取最佳风能质量并减少输电线路运营维护成本，风电场中风力机布局通常不足以使下游风力机风速重新恢复至初始来流风速[1]。由于目前风电场多采用单台风力机最大功率追踪策略，即各台风力机均处于零偏航状态，这种情况下尾流域相互叠加[2-3]，造成下游风力机见风速度严重下降，进而导致风电场全局出力的明显下降。考虑到风力机排布、地形粗糙度及大气湍流密度等因素，尾流效应所造成的平均功率下降可达2%～30%[4]，在大型海上风电场中可达10%～20%[5]。因此，为进一步研究如何减小风电场中尾流效应的影响，需要对其进行准确评估。

目前针对风电场尾流效应的计算主要包括2种方式，其一为通过专业的计算流体动力学(computational fluid dynamics，CFD)软件计算，其二为通过数学解析模型进行尾流场计算。由于CFD软件计算量极大，耗时较长，很难应用于实际工程迭代优化问题[6]。而解析模型计算量小且结果较为准确，近年来得到了广泛研究与应用。这类解析模型主要包括Jensen模型和高斯模型[7]。其中，Jensen尾流模型于1983年由N. O. Jensen[8]首次提出，其假设尾流区域线性扩张，呈“高帽”形。但实验结果表明该模型会低估风力机轮毂高度尾流风速，高估尾流域边缘处尾流风速[9]。1988年G. C. Larsen[10]提出的高斯模型将风速亏损假设为高斯对称分布，更加符合实际情况。基于上述模型，M. Bastankhah与F. Porte-Agel[7]在高斯模型的基础上引入质量与动量守恒，并加入初始湍流密度影响因素构建了数学模型。通过将其与LES模拟数据比较，发现该解析模型能够较为准确地评估尾流场风速，但并未考虑叶片后湍流密度的增加。T. Ishihara等人[11]引入风力机偏航角对尾流域影响及湍流变化，构建了风力机在偏航状态下其叶片后尾流场风速亏损及湍流密度变化数值分布情况，但该模型只考虑了单尾流，而未考虑风电机组之间的尾流叠加作用。本文在文献[11]的基础上引入尾流叠加效应，构建多尾流数学模型并进行海上风电场尾流效应评估及偏航优化研究。

目前针对风电场由于尾流效应造成的出力下降问题主要采取2种优化策略，其一为利用尾流计算模型进行风电场选址及布局优化，其二为利用上游风力机偏航控制实现尾流域的偏转，使下游风力机躲开尾流域风速亏损尖峰区域，以实现全局出力的提升[12]。目前针对第一种策略应用研究较多,但该方法主要受风向角变化影响，在风向变化频繁、风向角分布较为均匀的风电场中效果不佳，且受规划用地面积，投资及维护成本等条件的限制。同时，在已建成的风电场中这一优化方法同样不适用。因此近年来偏航角控制优化方法引起关注，其核心思想是：对位于来流风上游位置风力机进行偏航，令其后尾流域发生偏转，从而使位于下游位置风力机躲过前序风力机尾流尖峰区域，获得下游风力机出力提升。但偏航状态下风力机捕获风能能力下降，故上游风力机虽不受尾流效应或受尾流效应影响较小，仍会因偏航造成出力下降。因此，偏航策略应综合考虑各种因素以达到最优出力。目前针对该问题研究相对较少，在国内外尚处初始研究阶段。T. Ahmad等人[13]利用粒子群算法对法国SWV风电场2台风电机组计算最优偏航角下功率提升，结果发现通过偏航上游风力机，可实现2机组5%以上的整体出力提升，但该研究未扩展至多台机组情况，且未探究不同风力情况与偏航效果的关系。赵飞等人[14]利用张家口市坝上地区实测数据计算了偏航状态下2台机组出力变化。结果表明在该条件下，通过偏航控制策略，最多可实现2台机组整体功率17.6%的增长，但该研究仅说明了偏航策略对提升机组出力的可能性，而没有探究如何得到最优偏航角这一问题。由于该问题是一个高维全局优化问题，可考虑类比同为高维优化问题的风力机布局优化，采用元启发式算法进行寻优。其中，遗传算法在风力机布局优化问题中表现出良好的全局优化性及鲁棒性[15-16]。因此，本文针对尾流效应导致的出力下降问题，提出基于遗传算法的最优偏航策略以获得各风电机组最优偏航角，并通过具体算例分析了不同风力情况下最优偏航策略的变化规律及其对风电场的出力提升效果。

本文首先利用荷兰Borssele风电场实测风力数据对该地点风力的方向和速度进行建模，并在T. Ishihara提出的单尾流模型[11]基础上引入尾流叠加效应，同时考虑尾流效应导致的不同位置风力机功率及推力系数的变化，利用MATLAB搭建三维高斯多尾流模型。在此基础上引入蒙特卡洛随机抽样，提出一种基于蒙特卡洛抽样的风电场尾流效应评估方法，并对9台风力机(布局为“3×3”)小型风电场进行风速亏损计算及出力缺损评估。然后为减小尾流效应造成的出力缺损，本文将偏航理论同遗传算法相结合，提出一种基于遗传算法的风电场最优偏航策略，以获得最优尾流偏转效果；并在不同来流风条件下利用该策略对前述风电场进行出力优化。最后分析不同风向和风速下最优偏航策略对风电场的出力提升效果。

1 研究框架

为研究尾流效应对风电场出力的影响，本文首先构建风向、风速及尾流等数学模型，然后利用蒙特卡洛抽样方法获得随机风力数据，进而利用抽样所得数据进行出力评估，形成基于蒙特卡洛抽样的风电场尾流效应评估方法。接着，提出一种基于遗传算法的最优偏航策略，利用偏航角导致的尾流偏转减小风电场尾流效应。在综合考虑风速、风向等环境因素及风力机偏航角限制条件的基础上，利用遗传算法对风电场全局出力进行优化，并定量分析该策略的有效性。最后通过设定不同风力条件进行偏航角策略影响因素的分析。本文总体研究框架如图1所示。

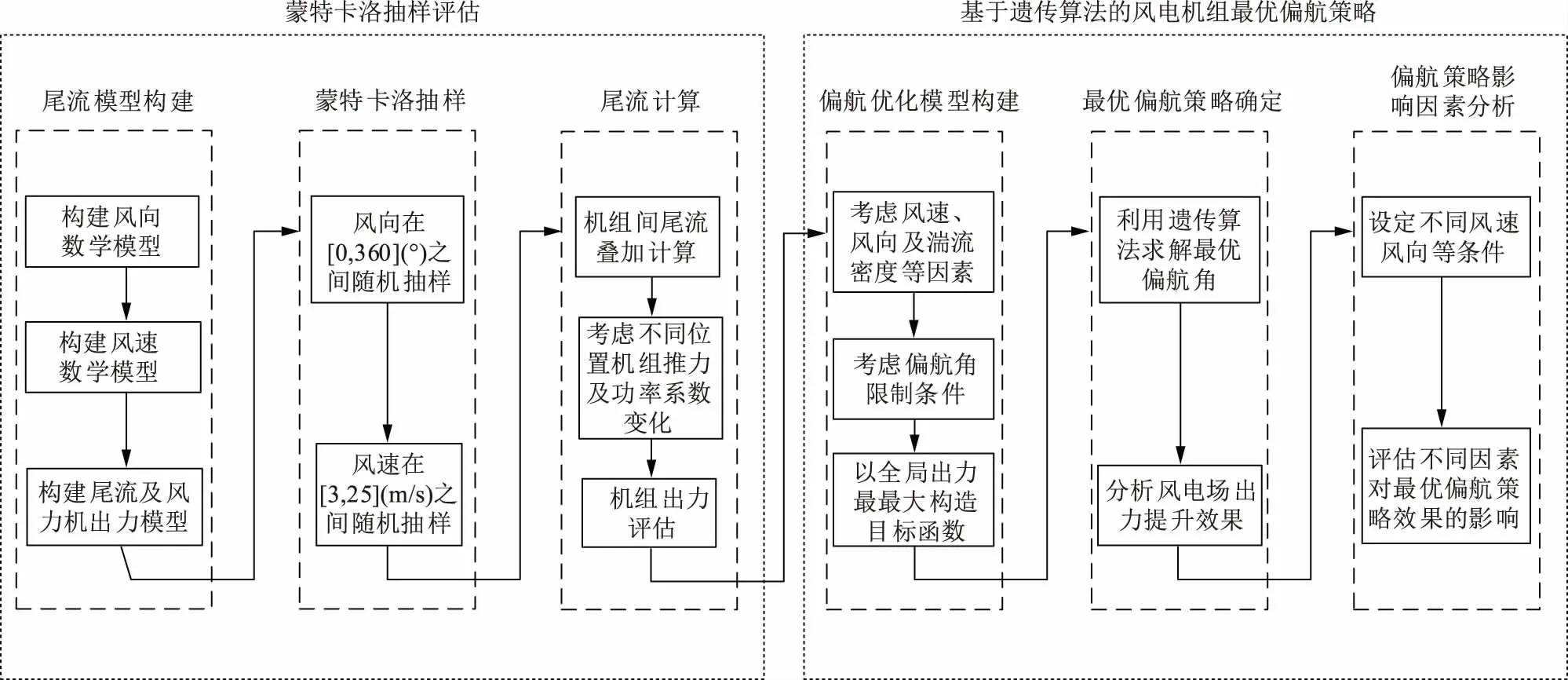
图1 本文研究框架Fig.1 Research framework of this paper

本文对尾流效应评估方法及偏航策略进行理论分析及实验验证，为其在工程中实际应用提供了科学的理论依据。同时，对偏航策略的定量及影响因素分析为其在工程应用中提供了理论指导，弥补了现有研究在此领域的不足。

2 风场数据及尾流模型

本文选用风力机单台容量2 050 kW，所用风力数据来自荷兰Borssele海上风电场II区实测数据[17]。

2.1 风电场概述

本文所研究风电场为“3×3”布局小型风电场，总装机容量为18.45 MW，各风力机轴向间距6d0，翼展方向间距为4d0，其中d0为风力机叶片直径。所用风力机轮毂高度为80 m，叶轮直径为82 m，切入风速、额定风速与切出风速分别为3.5 m/s、12.5 m/s与25 m/s。该风力机功率因数系数CP与推力系数CT随风速变化曲线如图2所示，可表征风电机组性能，其中该风力机功率因数最大值为0.465。

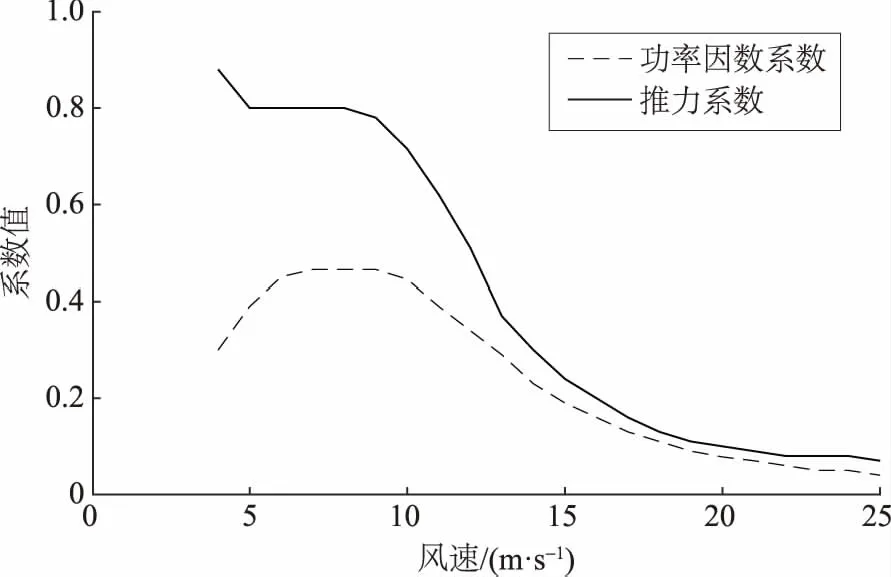
图2 风力机功率因数系数及推力系数曲线Fig.2 Power and thrust coefficient curves of wind turbines

本文所用风力数据的风玫瑰图如图3所示，其数据采集装置设置高度与轮毂高度一致。该图表明，Borssele风电场II区主要风向为西南风，主要风向角θmain=210°～240°。

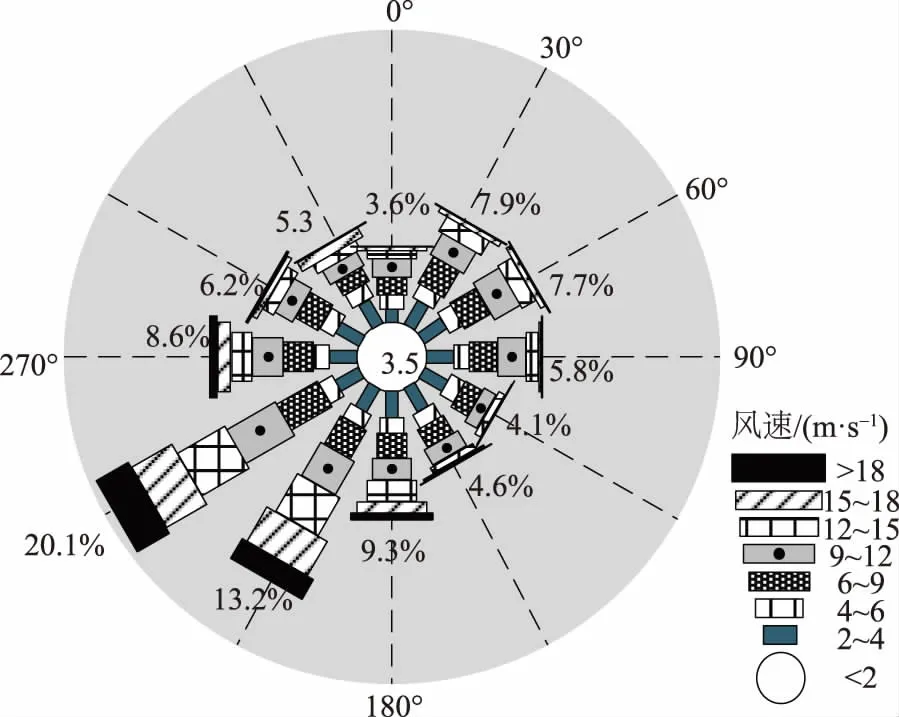
图3 Borssele风电场II区80 m高度风力平均数据Fig.3 Average wind data of Borssele wind farm zone II (height: 80 m)

2.2 风力模型

利用2.1节所述风力数据分别构建风向及风速数学模型。Von-Mises分布是对正态分布的圆形模拟[18]，而风向概率模型是对来流风向角θ自0°至360°的概率描述，因此风向概率分布通常描述为多个Von-Mises分布的叠加[19]：

(1)

式中：μh和κh分别代表第h次分布的平均方向和集中参数；I0为大气湍流密度；ωh为不小于0的第9次分布权重系数，且有

(2)

根据文献[19]研究结果，当H取3时已能够较为准确地描述实际风向分布，当H继续增加时会使后续计算更为复杂。故为保证准确性并节约计算成本，本文中H取为3。利用最小二乘法对数据进行拟合，可得各次分布的参数见表1。

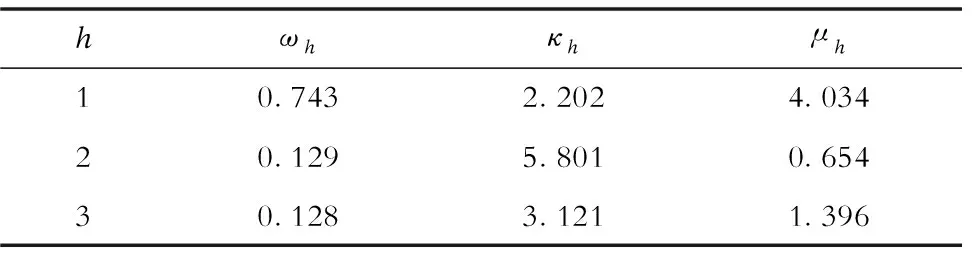
表1 基于3次Von-Mises分布的风向概率模型拟合参数Tab.1 Fitting parameters of wind direction probability model based on a mixture of three Von-Mises distributions

本文风速概率分布模型采用被广泛应用的Weibull分布[20]，同时经过比较发现，在不同来流风向下，风速概率分布并不相同。因此，为提高模型准确性，将风向分为12个子区域，分别对每个区域风速数据进行拟合。利用Weibull分布可得风速v的概率分布函数[21]：

(3)

式中k和c分别为形状参数及尺度参数。根据不同的风向子区域，拟合结果见表2。

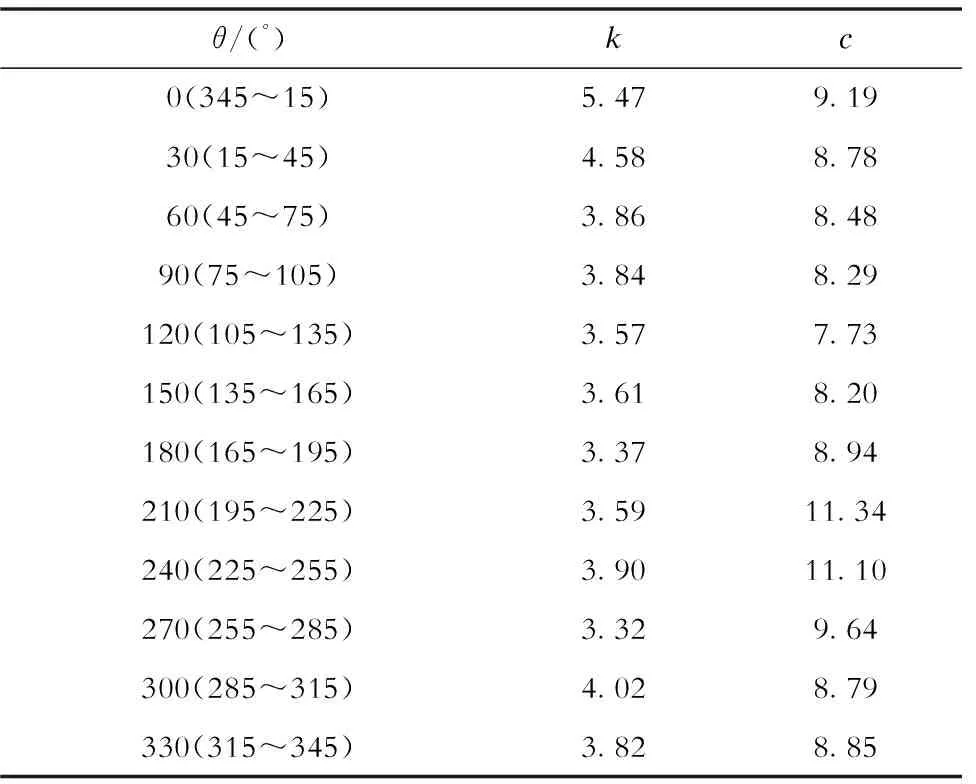
表2 基于Weibull分布的风速概率模型拟合参数Tab.2 Fitting parameters of wind speed probability model based on Weibull distribution

2.3 计及尾流效应的风电场出力计算

本文拟采用T. Ishihara等人[11]提出的偏航状态下单尾流模型并引入多尾流叠加。该模型将偏航风力机后风力缺损描述为相对该风力机叶轮中心偏移的高斯分布，同时将风力机后湍流密度增加量描述为一个双重高斯分布。由于大气湍流通常可以使偏航风力机后风向在其下游风力机处恢复原始来流风向，因此未考虑上游风力机偏航引起的风向变化。风力缺损可描述为[11]

(4)

式中：v0为初始来流风速；vw为计及尾流效应的下游处风速；F为标准化风速缺损最大值；C′T和Ia分别为偏航状态下的风力机等效推力系数及该风力机处的大气湍流密度；x为下游轴向距离；φ为高斯分布；r′为偏航状态下的尾流域横截面的辐射半径；σ为标准偏差；用上标′表示偏航状态的参数，下同。其中，C′T与r′分别表示为[11]

(5)

(6)

式中：z与y分别为竖直及翼展方向距离；γ为偏航角；yd为尾流偏移量，满足

yd=y′d+yd0.

(7)

式中首项和末项分别代表初始点后偏移量及初始偏移量，可分别计算为[11]:

(8)

(9)

式中：x0为初始远尾流域对应下游距离；α0为初始偏移角；σ0为初始标准偏差；k*与ε为增长与极限参数。

为获得更精确结果，在进行计算时，下游风力机处的单风力缺损计算为该风力机叶片平面上风速缺损二重积分的平均值。在有N台风力机的风电场中，计及多尾流效应的叠加，第i台风力机所受尾流效应而导致的风速缺损[15]

(10)

式中：aij为权重参数，当第i台风力机受第j台风力机尾流影响时取1，否则取0；Δvij为第j台风力机在第i台风力机处尾流效应所造成的风速缺损。

偏航状态下风力机出力PT将受到该风力机偏航角、见风速度及功率因数系数的影响[13, 22]，即

(11)

式中：ρ为空气密度；r0为风力机叶片半径。cos2γ即代表了偏航影响因子，当风力机处零偏航状态时其值为1。

考虑到不同位置处风力机功率因数系数及推力系数会因尾流效应而变化，造成风力机出力不同，并进一步影响各风力机后尾流情况，因此在计算中需对各台风力机功率及推力系数进行更新。

3 仿真分析

为了评估尾流效应所造成的出力缺损，首先计算在来流风向或风速变化时无尾流效应及有尾流效应2种情况下风电场出力变化。随后为更加准确评估实际情况下尾流效应对海上风电场出力影响，引入蒙特卡洛抽样方法，分别对风向及风速进行随机抽样并进行尾流计算。

3.1 单变量下风电场出力计算

为直观表现来流风向或风速对尾流效应的影响，分别假设各风力机处零偏航状态，且:①v0固定为10 m/s，改变风向从0°至360°;②来流风向角θ=90°，改变来流风速从3 m/s至30 m/s。可分别得到风电场在单变量下出力变化如图4(a)、(b)所示。

图4(a)表明，在“3×3”风场布局下，风电场出力在某些角度下会下降严重，同时其变化关于180°风向角对称分布。全局出力最低值发生在来流风向角θ=0°及θ=180°时，此时风电场出力下降5 442 kW，效率下降达42.9%。在θ=270°和θ=90°时也有明显的出力下降，可达4 528 kW。这2种情况对应来流风向与风电场列或行平行，此时上游风力机尾流尖峰区恰处下游风力机处，因此在尾流叠加下机组出力下降最为严重。图4(b)表明，尾流效应会使风电场等效切入及额定风速增大，使在相同风速条件下风电场出力下降，同时可使风电场达额定出力的风速区间变短。但其对切出风速影响较小，且使得机组在达到切出风速后出力下降更为缓慢。

3.2 蒙特卡洛抽样评估

风电场出力易因风力波动而大幅波动，因此可利用蒙特卡洛方法，通过对风向风速变量的随机抽样来较为准确地模拟实际情况[23-25]。其流程框图如图5(a)所示，尾流计算流程框图如图5(b)所示。

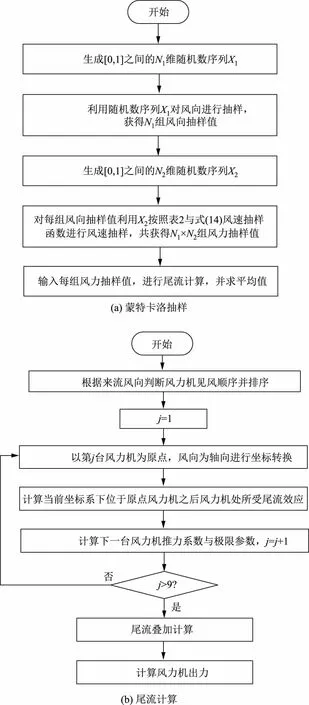
图5 基于蒙特卡洛抽样的尾流效应评估流程框图 Fig.5 Evaluation flowchart of the wake effect based on Monte Carlo sampling

风速的随机抽样函数可由其分布函数的反函数得到。式(3)所示风速概率模型的分布函数可表示为[26]

(12)

根据反变换法，取数值在0～1之间的n个随机数序列{rs},s=1,2,…,n，则风速的随机抽样函数

vs=c[-ln(1-rs)]1/k.

(13)

考虑到rs与(1-rs)同为在[0,1]取值，因此上式可化简为[26]

vs=c[-ln(rs)]1/k.

(14)

风向的拟合函数反函数求解过于复杂，因此本文中对风向随机抽样采用对式(1)的分布函数进行插值求得。每次蒙特卡洛抽样过程分别对风向随机抽样数N1=100，并对每次抽样所得风向角对应风速分布随机抽样数N2=100，可得到100×100组二维风力数据。利用抽样所得风向与风速数据分别由式(11)与图5所示流程图进行计算。重复10组该过程以更准确观察尾流效应导致的出力缺损情况，可得到结果见表3，其中每组结果均为利用该组抽样所得10 000组风力数据计算结果的平均值。表3中G为抽样组别，Pnowake为不计尾流效应的风电场出力，Pwake为计及尾流效应的风电场出力，ηwake为计及尾流效应的风电场效率，ΔPdown和Δηdown分别为出力及效率降低值。

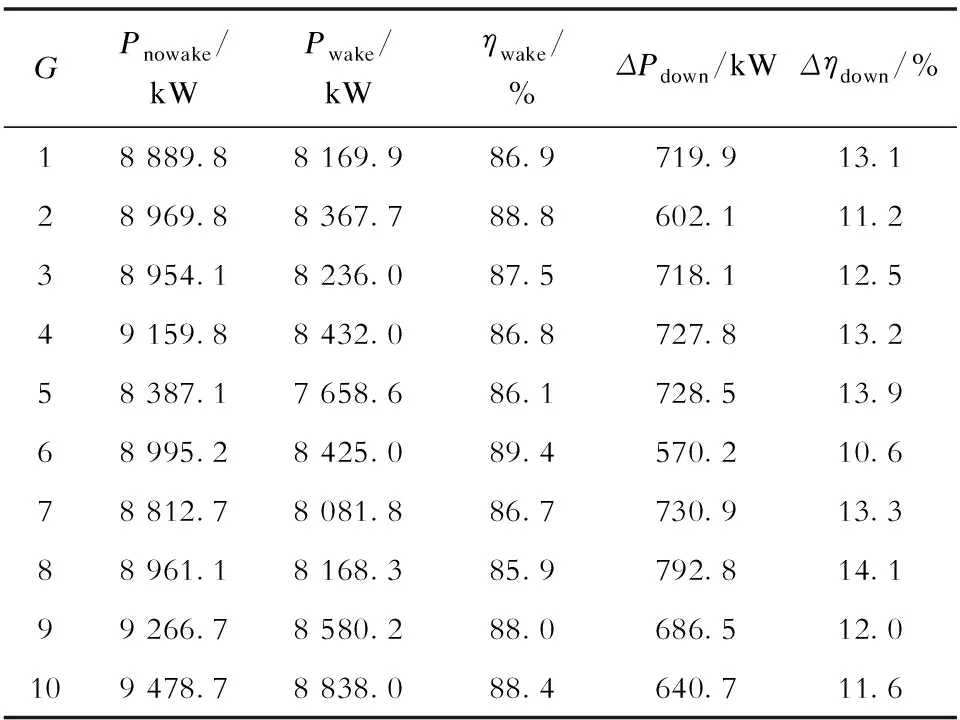
表3 蒙特卡洛抽样评估结果Tab.3 Evaluation results of Monte Carlo sampling

由表3可见，由于蒙特卡洛抽样方法的随机性，每组的结果并不相同。其中，由于尾流效应而造成的全局风力机出力缺损最大值达到了792.8 kW，最小值为570.2 kW，尾流效应所造成的效率下降均达到了10%以上，平均效率下降达12.55%。由于本算例所用风力模型的主要风向区间为210°～240°，而在此区间内尾流效应较小，因此利用蒙特卡洛抽样方法所评估的机组出力下降远小于前文所述θ=180°时的数值。同时，本算例仅考虑“3×3”风电场，而大型风电场中风力机数目多，尾流叠加更为严重，因此在大型海上风电场中由于尾流效应而导致的出力缺损将更加明显。

3.3 基于遗传算法的最优偏航策略

为分析偏航控制对由尾流效应造成的风力机出力下降的影响，将“3×3”风电场分为3列，每列偏航相同角度，且由于最后一列风力机已处于最下游位置，因此不需偏航控制。分别假设来流风向为90°与95°，来流风速10 m/s，γ1与γ2分别为上游2列风力机偏航角，计算上游2列风力机不同偏航角下整体风电场出力则可得到功率平面如图6所示。

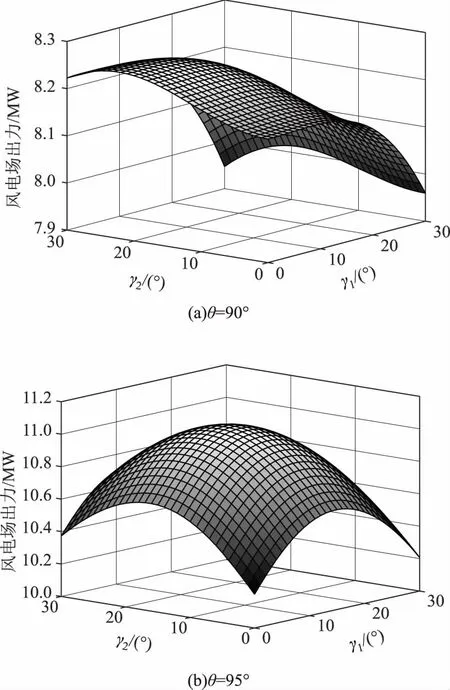
图6 风电场出力平面Fig.6 Output power planes with yawing

由图6可见，当处于尾流效应最严重状况之一(θ=90°)时，风电场在零偏航状态下出力为8 162 kW，而最优偏航策略下出力只为8 253 kW，出力提升仅有91 kW。这是由于此时下游风力机较难躲过上游尾流尖峰区域，获得出力提升较小。而为使尾流域达到足够偏转，上游风力机所需偏航角较大。此时由式(11)可知，本该不受尾流效应影响或影响较小的上游风力机出力将大幅下降。因此，这种情况下，由偏移策略得到的下游风力机出力提升难以有效弥补上游风力机偏航引起的出力下降，从而无法有效提升全局出力。而当来流风向自θ=90°偏转，例如θ=95°，此时下游风力机本身已躲过尾流效应最大值处，因此偏航策略可以更加有效地使其躲过尖峰区域，获得更大的出力提升。

随后，为得到最优偏航策略，在前文所述偏航状态下多尾流模型的基础上，提出一种基于遗传算法的最优偏航策略，其目标函数为

(15)

式中：P0为未受尾流效应影响且未偏航时的单台风力机出力；Pi(γ)为考虑尾流效应及偏航时的各台风力机出力。由于偏航策略应针对所有上游风力机，因此待优化变量设为末尾3位(对应下游3台风力机)为0的9维变量

γ=(γ1,γ2,…,γl，0，0，0),

l=1,2,…,6,

(16)

其中l按照当前风向下各风力机见风顺序先后编号，上游风力机编号在前，下游风力机编号在后。同时，研究[27]表明最优偏航角取值通常在0°～30°之间，因此约束条件为

0°<γl<30°.

(17)

为节约计算成本并保证准确度，遗传算法中群体大小取为100，终止迭代数为300，交叉概率为0.8，变异概率为0.4[16]。

按照以上条件分别对不同来流风力情况进行迭代优化。由于所用风力机切入风速为3.5 m/s，因此初始风速设为5 m/s。假设来流风向θ=95°，当改变风速时可得到此风电场最优偏航角策略如图7所示，出力提升结果见表4。表4中Pyaw为最优偏航策略下风电场出力，ΔPup和Δηup分别为最优偏航策略下的出力及效率提升值。

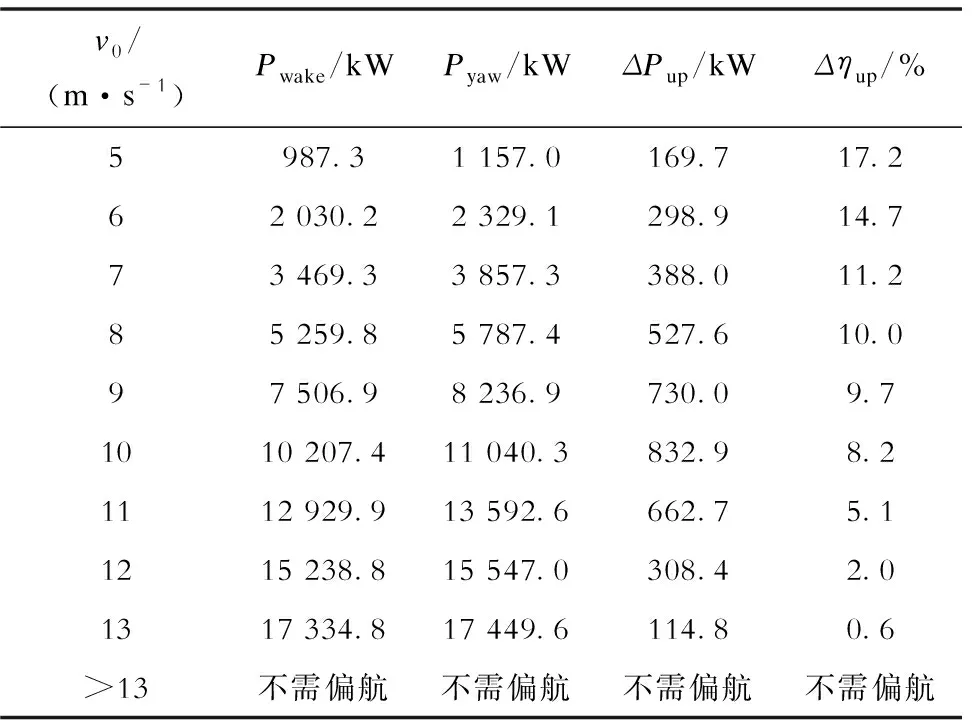
表4 不同来流风速下偏航策略优化结果Tab.4 Optimization results of yawing strategy with different incoming wind speeds

由表4可见，在切入风速附近，由于此时风速小，风力机出力小，虽效率提升明显，但由最优偏航策略可获得的整体出力提升并不大。而随着来流风速的增加，通过对上游风力机的适当偏航可获得下游风力机见风速度的大幅增加，从而使风电场获得显著的出力提升。当风速为10 m/s时，可获得832.9 kW的出力提升，但效率提升随风速增加呈下降趋势。当来流风速接近切出风速时，最优偏航策略效果下降明显，当大于某一风速值时，利用最优偏航策略不再能获得出力提升。

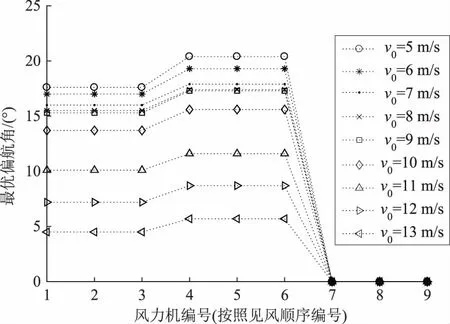
图7 最优偏航角变化图Fig.7 Variations of the optimal yawing angles

由图7可见，当风向一定时，依据见风顺序可将风电场划分为若干组，且每组在某一风速下的最优偏航角非常接近。在最优偏航策略可用范围内，上游各风力机偏航角大小与风速负相关，在某些风速情况下，上游风力机较小的偏航角即可带来较大的出力提升。当来流风速在5 m/s至10 m/s之间变化时，各组最优偏航角变化幅度较小。随着风速进一步增大，所需最优偏航角迅速变小。而当风速较高时，尾流效应较弱，且偏航引起的尾流偏转较小，因此偏策略航效果不佳。

考虑在不同来流风向角及风速情况下最优偏航策略可获得的出力提升，分别以来流风速、来流风向角及出力提升为坐标轴，并从来流方向角坐标轴正反2个方向作柱状图，其结果如图8所示。

如图8所示，当来流风向角为90°时，无论来流风速高低，利用最优偏航进行尾流偏转获得的全局出力提升十分有限，最大仅约100 kW，明显少于其他情况，说明此时最优偏航策略获得的下游风力机出力提升难以有效弥补上游风力机偏航引起的出力下降。而当从最严重情况之一的来流风向角 (θ=90°)偏转一定角度后，偏航策略的效果将更为明显，风电场整体出力能够得到有效提升。但当风向角偏转至较为良好的情况，此时风力机间尾流区域重叠不大，利用偏航策略使尾流区偏转获得的下游风力机出力提升无法有效弥补上游风力机偏航造成的出力下降，偏航策略效果不佳。在进行优化的情况中，当θ=92.5°、来流风速为10 m/s时，利用偏航策略优化该风电场可获得1 035 kW的出力提升，相较未偏航状态效率提高11.8%。

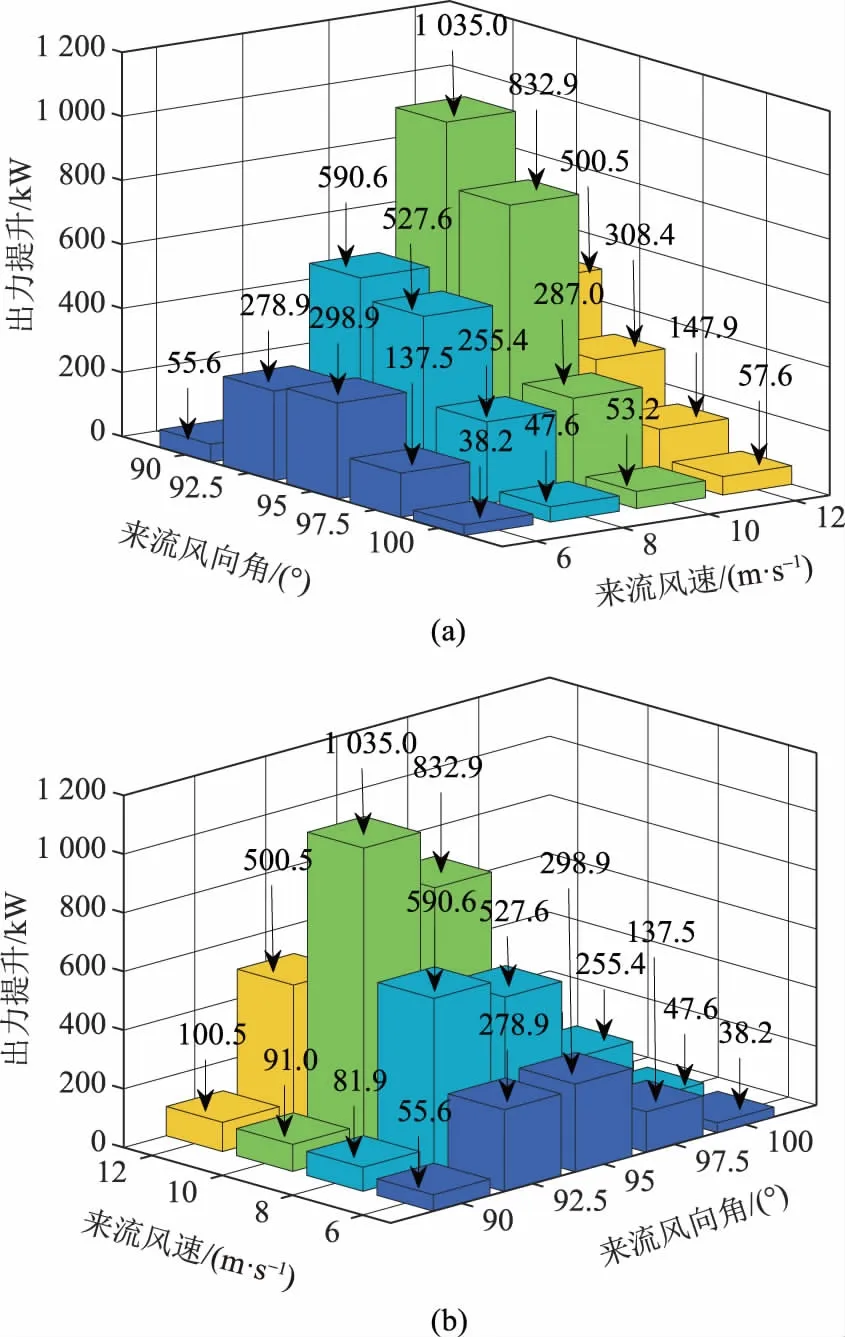
图8 最优偏航策略下出力提升Fig.8 Output power improvement with optimal yawing strategies

4 结束语

a)对现有尾流模型引入尾流叠加，进而提出一种基于蒙特卡洛抽样的尾流效应评估方法，并利用荷兰Borssele海上风电场实测风力数据进行算例分析。结果表明风电场会因尾流效应造成明显出力下降。

b)提出一种基于遗传算法的最优偏航策略，利用偏航角引起的尾流域偏转减小风电场尾流效应，从而获得风电场全局出力提升，并探究偏航效果与风力情况的关系。结果表明，在一定风速范围内，风电场可利用最优偏航策略获得显著出力提升，且最优偏航角与来流风速负相关。研究过程中发现遗传算法仍存在如计算时间长等问题，因此后续工作准备采用其他元启发式算法进行对比，并对寻优方法进一步改进。

c)经过不同风力情况下的偏航优化发现，需要偏航的风力机主要由风向决定，而风力机的最优偏航角主要由风速决定。考虑到风力的多变性与随机性，可利用前备数据提前进行优化并将数据制表存储，系统现场根据当前风力情况查表以获得实时最优偏航控制策略。