蒙特卡洛法在风电场架空输电线路绕击跳闸率计算中的应用

刘正富，骆潘钿，王朋，朱良合，苏雷涛

(1．广东电网有限责任公司电力科学研究院，广东 广州 510080；2．南方电网电力科技股份有限公司，广东 广州 510080)

建于山区、丘陵的风电场由于地质、气象原因，属于雷击重灾区。雷击风电场输电线路导致风电场跳闸在风电场停电、设备损坏事故中占据相当大的比例，严重影响风电场运维。此外我国输电线路运行经验表明，雷击也是各种引起跳闸的原因中危害最大的[1-5]。雷击事故主要分为反击事故和绕击事故。随着特高压输电线路的发展，系统内部绝缘增强，在特高压线路的运行中绕击事故占雷击事故的绝大多数[6-8]。因此，亟需准确计算风电场输电线路绕击概率并评估其耐雷水平，指导风电场输电线路绝缘设计，提高风电场及输电线路防雷水平，保障风力发电，保护风电场设备。

目前，用于架空线路绕击概率计算的仿真模型主要有电气几何模型(electrical geometrical model，EGM)、先导发展模型等。EGM较符合实际运行经验，但EGM中未考虑放电的随机性，其大地击距、导线参数选取需提前完善；先导发展模型采用简化的二维电场模型，可模拟被击目标的先导发展和竞争，但与实际的电磁场存在一定差距。本文运用基于EGM闪络判据的蒙特卡洛法计算输电线路的绕击跳闸率。蒙特卡洛方法基于“随机数”模拟事件过程，利用计算机能够快速、重复计算的优势进行大量计算，以计算结果发生“频率”对应实际发生“概率”[9-10]。本文通过对雷电流各个随机变量的选取以及雷击输电线过程的建模，来模拟雷击输电线路的随机性，相比于现有方法更能反映实际雷击情况[11-16]。运用蒙特卡洛法反复循环计算过程中，以改进EGM作为雷击部位判据，在传统EGM基础上考虑先导入射角的概率密度分布，反映负保护角时仍发生雷击的现象；以耐雷水平作为闪络判据，采用绝缘子50%闪络电压来确定其耐雷水平，判断绝缘是否闪络[17]。

本文运用蒙特卡洛法和改进的EGM，对风电场架空输电线路绕击跳闸率进行105以上次数的计算，仿真计算过程考虑风电场输电杆塔地面倾角、工作电压等影响因素。通过计算验证本文所述方法的有效性和准确性。

1 蒙特卡洛法计算变量的选取

变量的选取是运用蒙特卡洛法计算的关键，其合理性直接影响计算结果的可信度。运用蒙特卡洛法进行风电场架空线路绕击跳闸率计算时，考虑到山区、丘陵等雷电活跃地区的特殊性，选取关键影响变量(如雷电流幅值、雷电先导入射角、雷电空间坐标、输电线路的电压相位)时，应尽可能符合实际情况。

1.1 雷电流幅值

根据历史经验，雷电流大部分为负极性，且产生的绝缘破坏比正极雷电流大，因此本文计算主要针对负极性雷电流开展。参考IEEE标准，仿真计算时，当雷电流幅值小于20 kA时，取雷电流Ip的中间值Ipm=61.1 kA，lnIp标准差σlnIp=1.34；当雷电流幅值大于20 kA时，取Ipm=33.3 kA，σlnIp=0.61[18]。雷电流幅值可近似为对数正态分布[19-21]，为了便于随机数的选取，本文以对数正态分布模拟雷电流幅值分布区间，且Ipm=30.1 kA，σlnIp=0.76。经计算，随机产生1 200次符合对数正态分布的雷电流，模拟实际情况，其概率密度分布如图1所示。

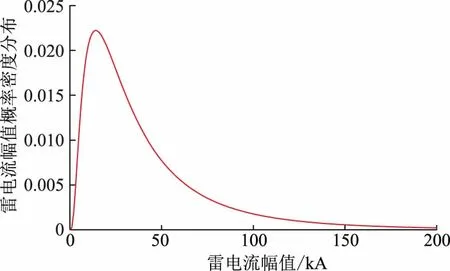
图1 雷电流幅值概率密度分布Fig.1 Probability density distribution of lightning current amplitude

1.2 雷电先导入射角

EGM中，雷电先导与地面垂直入射，然而实际雷击地面或导线时，雷电先导并不全是完全垂直于地面的。因此，对风电场输电线路雷电绕击进行仿真建模时，传统的EGM无法仿真负保护角时仍然发生绕击的工况。

本文基于传统的EGM，运用蒙特卡洛法进行计算，并引入先导入射角参数。实际雷电空间轨迹复杂，为简化雷电模型，设定地线击距的最高点为雷电偏转高度，即在此高度雷电先导开始受地面输电线路结构的电场影响并发生轨迹偏转。在此偏转高度之上则简化雷电模型，认为雷电垂直入射地面。

雷电先导入射角的影响和概率密度分布的计算参考Whitehead提出的先导入射角概率密度分布公式[22]：

p(φ)=Kmcosmφ.

(1)

式中：φ为雷电先导入射角，取值范围-90°～90°；p(φ)为先导入射角概率密度分布；m为形状参数，本文中m取3；Km为尺度参数，其值由归一化计算求得。m取不同值时的先导入射角概率密度分布如图2所示。

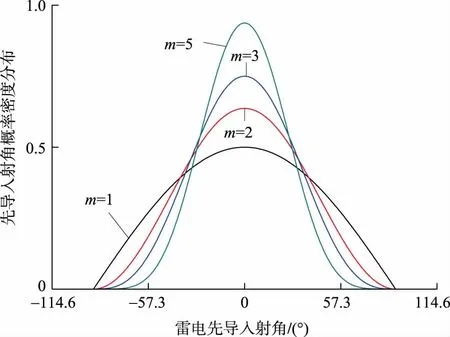
图2 先导入射角概率密度分布Fig.2 Probability density distribution of leading angle of incidence

将各参数值代入式(1)，得到雷电先导入射角φ的概率密度分布

p(φ)=0.75cos3φ.

(2)

1.3 雷电空间坐标

发生雷击时，当雷电落在输电线路两侧引雷宽度内时，可能会发生绕击输电线路，不同坐标位置发生输电线路绕击的概率不同。运用蒙特卡洛法进行输电线路绕击跳闸率计算时，需考虑雷电在线路两侧的引雷宽度内分布情况。本文仿真模型考虑雷电在线路两侧引雷宽度内呈均匀分布。

引雷宽度的计算采用美国防雷工作组提出的公式[8]：

{W}m=2{xg}m+4{hg}m1.09.

(3)

式中：W为风电场架空输电线引雷宽度；xg为架空输电地线水平坐标；hg为架空输电地线的平均高度。

1.4 输电线电压相位

风电场输电线路的瞬时电压值对绕击概率有很大影响。雷电绕击时，需考虑输电线路电压相位。雷击为随机概率事件，任何时刻都可能发生，因此发生输电线路绕击时，电压相位存在随机性。仿真模型中电压相位变量在0°～360°内均匀分布。

2 雷击部位及闪络判据

经过几十年的验证，EGM已经成为应用最为广泛的雷击部位判定方法。传统的EGM认为雷电通道始终垂直于地面发展，本文中考虑了先导入射角的概率密度分布，能够反映负保护角时仍发生雷击的现象。EGM的基本原理是通过几何方法构建地线、导线、大地的雷电击距范围：当雷电先导在击距范围之外，击中点不确定；当雷电先导到达某一物体的击距范围内，就会发生跃变进而击中该物体。如图3所示，雷电先导如果先到达导线暴露弧，则判断为雷击导线。图3中：设O点为架线杆塔的基础中心；在H高度雷电先导发生随机偏转；雷电通道1表示雷电先导偏转后击中地线保护弧AB，雷电通道2表示击中导线暴露弧BC，雷电通道3表示大地屏蔽区域CE。

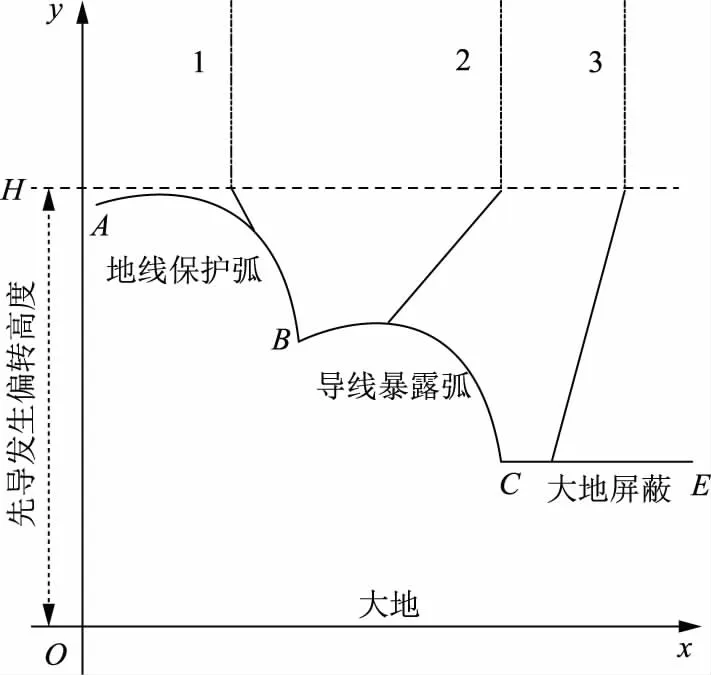
图3 引入先导入射角的EGM雷击部位示意图Fig.3 Schematic diagram of EGM lightning stroke part introducing leading angle of incidence

根据IEEE标准推荐公式，架空地线的击距

(4)

式中I为雷电流。

考虑线路瞬时工作电压u(t)后的导线击距[23]

(5)

击距系数对绕击跳闸率的影响很大，现有的击距系数公式只在一定范围内适用。本文中击距系数选用文献[24]的拟合公式，该公式便于运用于多回线路的击距系数的计算：

k=1.066-{h}m/216.45.

(6)

式中：k为击距系数；h为导线平均高度。

由于部分风电场输电线路位于山区或丘陵，地形对输电线路屏蔽性能影响很大，因此在EGM中引入地面倾角来反映地形的起伏。引入地面倾角后，需要对输入参数进行坐标变换。变换方法是以杆塔的地面中心点作为坐标的原点，如图4所示，进行x、y坐标旋转后，新的坐标为：

(7)

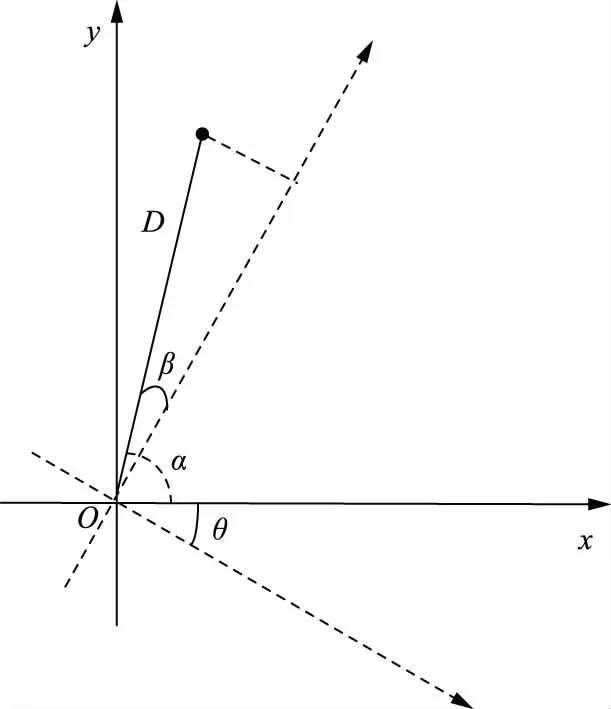
图4 引入地面倾角后坐标变换方式Fig.4 Coordinate transformation mode after introducing ground dip angle

式中：θ为地面倾角；D为导线距离中心点的距离；α为无地面倾角时导线、中心点连线与地面的夹角。

本文运用等值电流法建立绕击导线等值电路来计算绕击耐雷水平。考虑输电线路电压，当负极性雷电绕击输电线路时，等值电路如图5所示，绕击耐雷水平

(8)

式中：Umcos(ωt)为架空输电线路工作电压等效电源，Um为电压幅值，ω为角频率，t为时间；U50为架空线绝缘子50%负极性闪络电压绝对值；Z0为雷电流通道的波阻抗；ZC为输电线路波阻抗。

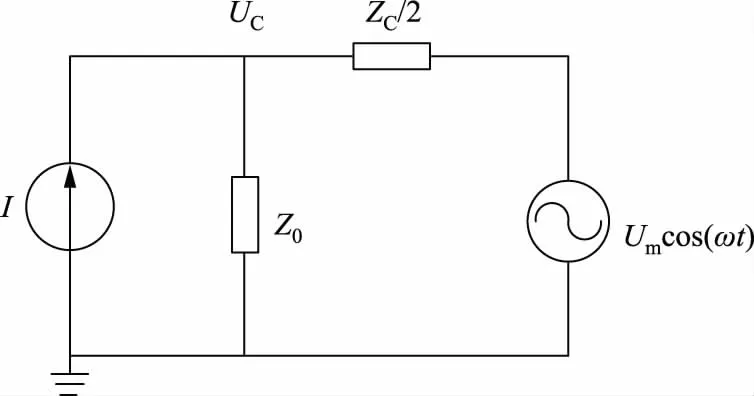
图5 绕击导线等值电路Fig.5 Equivalent circuit of shielding failure wire

3 仿真计算与结果分析

蒙特卡洛法用于风电场架空输电线路绕击仿真的流程如图6所示。

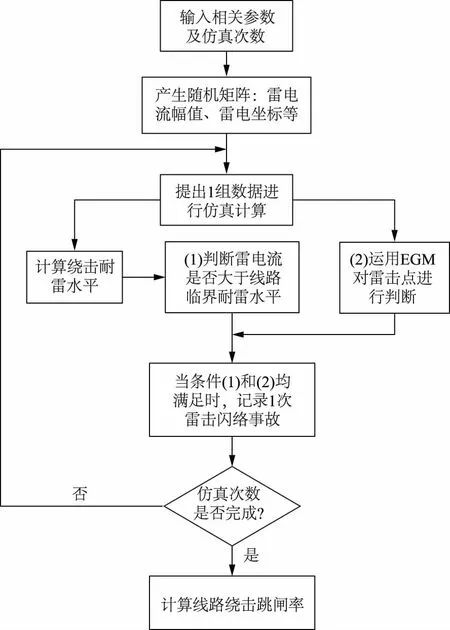
图6 蒙特卡洛法计算绕击跳闸率的流程Fig.6 Flowchart of calculating shielding failure trip-out rate by using Monte Carlo method

建模完成后，在计算机上采用蒙特卡洛法进行仿真计算，计算次数105以上。然后统计计算绕击跳闸率

(9)

式中：nflash为统计发生闪络的次数；n为总的仿真计算次数；Ng为落雷密度。

3.1 计算结果准确性评估

蒙特卡洛法的计算原理是基于大量的计算和数据统计来反映真实事件规律，因此计算结果的正确性与计算次数成正相关，为了得到较为明确的结果，需进行多次仿真。不同仿真次数对结果的影响如图7所示。

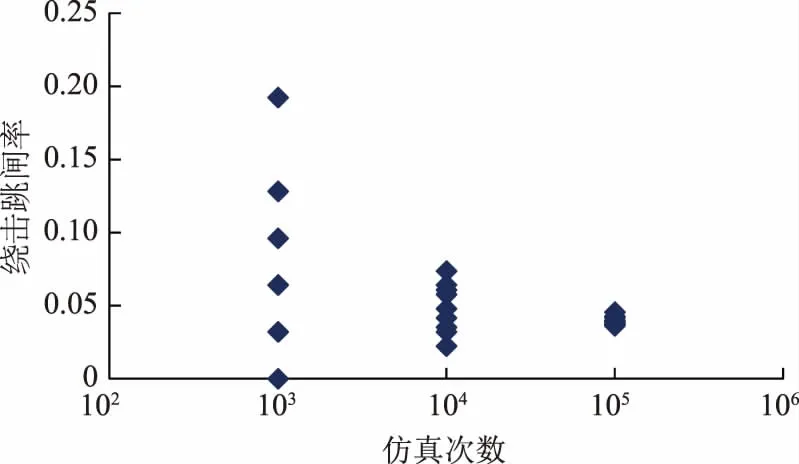
图7 仿真次数对计算结果的影响Fig.7 Influence of simulation times on calculation result

经计算，当仿真次数大于105时，计算结果的偏差在0.025以内，满足防雷计算的需求。因此本文采用蒙特卡洛法进行绕击仿真计算跳闸率时，仿真次数应设为105次以上。

为验证本文所采用蒙特卡洛法的准确性，分别采用EGM和蒙特卡洛法对110 kV-SJ2型同塔双回线路进行绕击跳闸率计算，杆塔结构参数如图8所示，计算结果如图9所示。

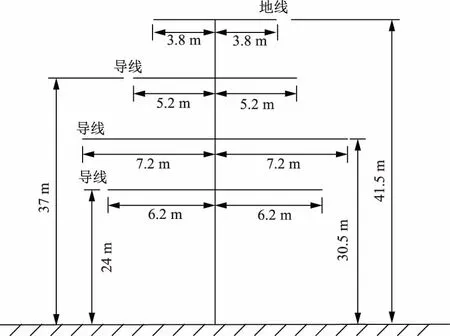
图8 110 kV-SJ2型三相输电杆塔结构参数Fig.8 Structure parameters of 110 kV-SJ2 three-phase transmission tower

由图9可以看出，2种仿真模型绕击跳闸率都随着地面倾角增大而增大，接近实际情况。但EGM中，地面倾角增大，暴露弧也会增大，导致绕击跳闸率计算结果相比于蒙特卡洛法偏大。运用蒙特卡洛法时，增加了雷电先导入射角的随机影响，雷电并不一定会击中导线，因此没有EGM敏感。从这一点来看，运用蒙特卡洛法更符合实际情况。

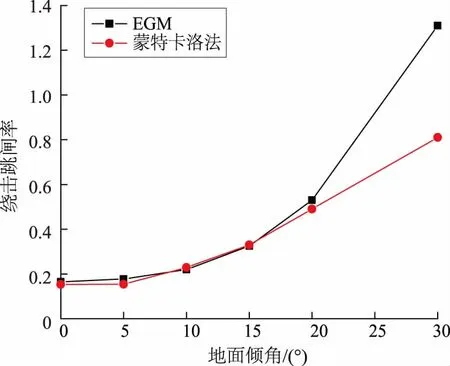
图9 地面倾角变化时，EGM与蒙特卡洛法计算结果对比Fig.9 Comparisons of calculation results of EGM and Monte Carlo method in case of ground dip angle changing

3.2 110 kV-SJ2杆塔绕击跳闸率计算

运用蒙特卡洛法，对大量仿真计算结果进行统计，绕击及闪络次数可反映线路耐雷水平。本文运用蒙特卡洛法对110 kV-SJ2型杆塔进行105次仿真计算，其中绕击次数为319次，绕击并闪络次数为313次，各相线路发生雷击点次数统计结果见表1。

表1 基于蒙特卡洛法的110 kV-SJ2杆塔绕击跳闸率计算结果Tab.1 Calculation results of shielding failure trip-out rate of 110 kV-SJ2 tower using Monte Carlo method

根据该型杆塔仿真计算统计结果，可针对性地优化杆塔参数，防止绕击，从而提高输电线路的防雷水平。

4 结束语

本文介绍了蒙特卡洛法在风电场输电线路绕击跳闸率计算中的应用原理及实现，针对山区、丘陵等雷击重灾区雷击输电线路的随机性，增加了雷电流幅值、雷电先导入射角、雷电空间坐标、输电线电压相位等随机变量的影响，以建立尽可能符合实际情况的计算模型。通过引入地面倾角来改进EGM，作为雷击部位判断的依据，并根据绕击导线等值电路来计算是否发生闪络。最后，对110 kV-SJ2杆塔输电线路的绕击跳闸率进行大量仿真计算，计算结果有助于指导线路绝缘的设计改进。

影响线路绕击跳闸率的不确定因素还有地质自然条件、湿度、温度、风速等。随着对雷电认识的加深和对实际风电场运行情况的了解，可以在蒙特卡洛法中逐步加入更多影响因素，建立合理的影响模型，使计算结果更加符合真实情况。