对一个猜想不等式的探究

浙江大学附属中学丁兰校区 (310021) 俞忠有 施刚良

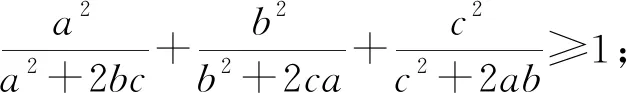
笔者本想去证明猜想不等式，思考了很长时间但证明不出来.于是就想能否将字母增加一个，变为4个可能会有新的思路(数学家在证三维彭加莱猜想时发现很难证，于是从四维、五维、更高维入手，发现都可以证明，最后，三维彭加莱猜想被俄罗斯数学家佩雷尔曼证明).通过等价转化命题再利用反证法，发现安老师提出的猜想不等式对4个字母的情况是能够加以证明的.

四元猜想不等式：已知a,b,c∈R+，且n∈N*，证明：

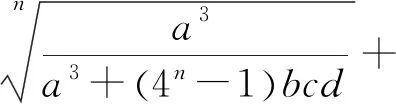
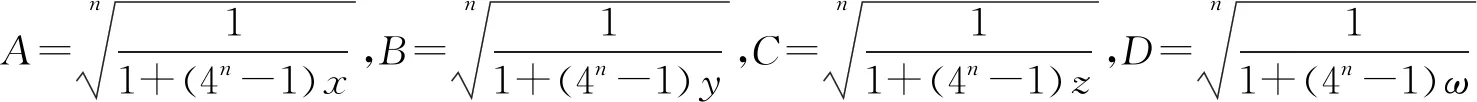
通过上面的铺垫，要证猜想不等式成立，只要证A+B+C+D≥1即可，其中(1-An)(1-Bn)(1-Cn)(1-Dn)=(4n-1)4(ABCD)n.

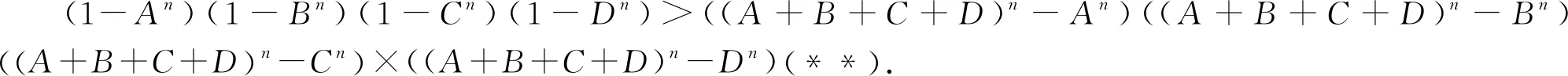
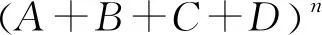
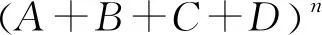
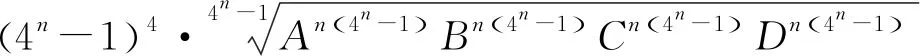
结束语：不等式问题的证明技巧性与多样性吸引着很多数学教师。本文的证明思路来自[2]，但文[2]没有证明4元不等式的情形，也没有提出m(m≥4)元不等式情形。本文完整地证明了4元不等式情形，按照上述证明思路，m元不等式也是成立的，但遗憾的是笔者仍不能直接证明4个字母情形的不等式，希望有兴趣的读者能给出该情形的直接证明(不是借助反证法)方法.