分类讨论思想在初中数学教学中的应用分析

孙大桂

【摘要】新课标指出：在数学教学中，要培养学生的数学思想，让学生能够运用数学思想、数学思维解决生活实际问题.而分类讨论思想，作为数学教学中的重要思想之一，有利于考查学生的综合能力和灵活应用能力，是培养学生综合思维的一种重要而有效的方法.为此，本文就分类讨论思想在初中数学教学中的应用价值、应用原则、应用路径进行了探索分析，旨在通过分类讨论思想在数学教学中的有机渗透，提高学生的问题解决能力和数学核心素养.

【关键词】分类讨论思想;初中数学;应用分析

分类讨论思想是一种最基本的解决问题的思维策略，旨在将所要研究的对象按照标准分为若干不同的类别，在逐个研究的过程中，达到分而治之的效果[1].在初中数学教学中，分类讨论思想贯串整个数学教学全部内容，包括概念、定理、公式、运算性质、不确定的量等内容，是培养学生良好数学思维品质的重要方法.为此，本文就分类讨论思想在初中数学教学中的应用进行了探究分析.

一、分类讨论思想在初中数学教学中的应用价值

（一）有利于培养学生的系统思维

分类讨论思想要求学生从多个角度、多个视角对问题进行分析、探讨、推测[2].在这个过程中，学生需要结合自己已掌握的知识点进行综合探讨，对教学内容进行梳理，使之条理化、逻辑化，将复杂问题通过归类转化，在分情况思考分析的基础上，化繁为简，看清问题的本质，促使问题得到有效解决.经过此过程学习、深化，不仅可以促进学生的思维发展，还可以培养其系统思维，从而提高学生的知识构建能力.

（二）有利于提高学生的问题解决能力

数学思想不仅是一种可以应用于学习阶段的学习思路，更是一种人与自然数量关系、空间关系的意识总结[3].换言之，数学思想是一种思维的结果，能够帮助人们系统化地看待世界和生活.在初中数学教学中应用分类讨论思想，从本质上看，是一种逻辑思维的方向，致力于解决数学各种小问题，还是一种重要的数学思想和解答策略，应用于各个模块中，体现了思路的多元化，对促进学生思维灵活发展，认识数学内容的客观规律具有重要的意义.可见，分类讨论思想在初中数学教学中的应用，对提高问题解决能力，认识数学学科魅力具有积极的促进作用.

二、分类讨论思想在初中数学教学中的应用原则

（一）层次性和互斥性原则

分类讨论思想在数学解题中有着广泛的应用[4].为此，在教学的时候，为提高分类讨论思想的应用价值，要遵从层次性原则，按照解题步骤和各个环节的对应要求，依次展开探索分析.而互斥性原则是指在分类讨论的过程中，所考虑的可能性之间不存在重复的关系，各自独立，没有交集.

（二）标准性和相称性原则

在初中数学教学中应用分类讨论思想的时候，为提高分类的精准性和有效性，在分类之前要遵从其标准性的原则，这样既可以做到周全思考，又可以形成良好的思考学习习惯.同时，在分类对象和分类问题的时候，要遵从其相称性原则，也就是说对象和问题是相对的，在一一对应的基础上，把握分类讨论思想的科学性和步骤性，避免分类出现交集和重复，从而提高问题的解决质量.

三、分类讨论思想在初中數学教学中的应用路径

（一）利用分类讨论思想认识函数

函数是初中数学教学的重点、难点，占据中考半壁江山.而分类讨论思想在函数教学中有着较高的应用价值，既可以提高对函数性质的理解，又可以实现函数的灵活应用.因此，为了使学生能够掌握和消化函数知识点，培养其分类讨论思想非常关键.

例如，“一次函数”教学中，在判断函数是增函数还是减函数的时候，就需要学生运用分类讨论思想进行综合考虑.

又如，一次函数y=kx+b，当1≤x≤4时，3≤y≤6，则bk的值是.

在解析这一填空题的时候，教师要让学生分析一次函数的增减性与什么有关.在激活思维的基础上，回归题意，题中给出了一次函数中自变量的取值范围，但是并没有明确指出该函数是增函数还是减函数，为此，在解析的时候，就要结合k>0，k<0这两种情况进行分析.在分类讨论的基础上，培养学生综合思维能力，深化其所学知识内容.

再如，一次函数在实际应用中的分类.

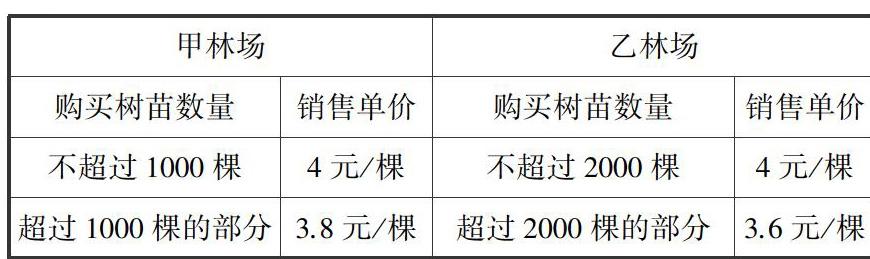
为改善生态环境，防止水土流失，某村计划在江汉堤坡种植白杨树，现甲、乙两家林场有相同的白杨树苗可供选择，其具体销售方案如下：

设购买白杨树苗x棵，到两家林场购买所需费用分别为y甲，y乙（元）.

（1）该村需要购买15000棵白杨树苗，若都在甲林场购买所需费用为多少？若都在乙林场购买所需费用为多少？

（2）分别求出y甲，y乙与x之间的函数关系式.

（3）如果你是该村负责人，应该选择到哪家林场购买树苗合算，为什么？

在解析第（1）问的时候，只要根据单价x数量就可以得出购买树苗所需要的费用，但是在问题（2）（3）的解析中，就要引导学生进行分类讨论，根据图表和题意所示，让学生分别按照0≤x≤1000，x>1000，0≤x≤2000，x>2000进行分段考虑，在（3）的解析中，同样按照其分类讨论表示关系.学生通过分类讨论对比思考，选出正确的答案.这样不仅提高问题解析的精准性，又可以促进学生学以致用，使其体会函数在日常生活中的应用价值.在分类讨论思想与函数有机整合的过程中，提高函数教学质量.

（二）利用分类讨论思想探索方程知识

对于初中数学，解方程是考试必考的知识.但是，在解方程的过程中，也会存在一些容易忽略的问题，导致其结果不完整.因此，为提高学生掌握这一基础知识，使其认识分类讨论思想在方程知识中的应用价值，在教学的时候，教师可以结合分类讨论思想，通过问题引导的方法，促进学生有效解决方程问题，从而提高学生思维的灵活性和发散性.

在教学“一元二次方程”时就会应用到分类讨论思想.

例如：已知关于x的方程m2x2+（2m+1）x+1=0有实数根，求m的取值范围.

在解析这一问题的时候，教师可以让学生思考：在题意中有没有指明是二次方程？在这个基础上，让学生考虑该方程是一次方程的可能，然后根据两种情况：“是一（或二）次方程”和“有实数根”，结合二次项系数是否为零进行分类讨论，得到：

①当m2=0，即m=0，方程为一元一次方程，即x+1=0，有实数根x=-1;

②当m2≠0，即m≠0，方程为一元二次方程，由有实数根的条件得Δ=（2m+1）2-4m2=4m+1≥0，

m≥-14，

所以m≥-14，且m≠0.

通过分类讨论思想的有效应用，学生知道在解析方程时，首先要明确讨论的对象;其次要进行合理分类，符合分类的标准原则、周全原则、独立原则;最后，对问题进行归纳，得出结论.分类讨论思想渗透方程问题的整个解决过程，既可以加深学生学习方程的印象，又可以使其掌握解决方程问题的方法，从而使学生形成严谨、科学的学习习惯.

（三）利用分类讨论思想解析动点问题

动点问题一直以来都是中考的难点和学习的重点，要解决动点问题，学生需要具备灵活的思维能力，能够根据问题进行分类讨论，并在动态变化的过程中认识问题本质，发现其中的运动规律，从而实现有效解决问题.因此，为了渗透分类讨论思想，提高初中数学教学效果，可以将此思想应用于动点问题探索中.

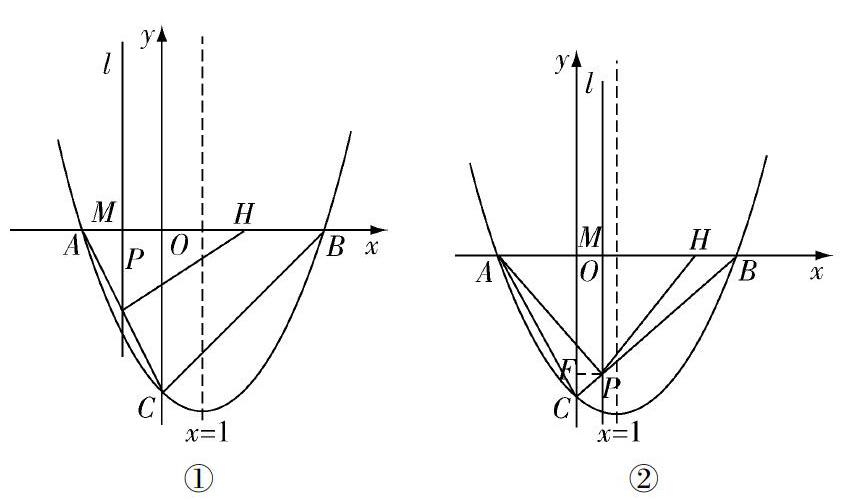
例如，如图，在平面直角坐标系中，抛物线y=ax2+bx-4与x轴交于点A（-2，0）和点B，与y轴交于点C，直线x=1是该抛物线的对称轴.

（1）求抛物线的解析式.

（2）若两动点M，H分别从点A，B以每秒1个单位长度的速度沿x轴同时出发，相向而行，当点M到达原点时，点H掉头并以每秒32个单位长度的速度向点B方向移动，当点M到达抛物线的对称轴时，两点停止运动，經过点M的直线l⊥x轴，交AC或BC于点P，设点M的运动时间为t秒（t>0），求点M的运动时间t与△APH的面积S 的函数关系式，并求出S的最大值.

在求解这一问题的时候，解析问题（1）只需要学生结合抛物线y=ax2+bx-4与x轴交于点A（-2，0），直线x=1是该抛物线的对称轴等数学信息，通过联立方程组便可以求解.但是，对于问题（2）动点问题，则需要学生考虑实际情况，分类进行讨论，在此过程中，教师可以引导学生运用分类讨论思想进行探索：

由于点M到达抛物线的对称轴时需要3秒，所以t≤3.又当点M到达原点时需要2秒，且此时点H立刻掉头，所以可分两种情况进行讨论：

①当0

通过分类讨论思想在动点问题中的指导应用，使得学生在解析问题的时候，能够全面分析影响因素，做到高效解题.分类讨论思想的运用可以提高学生的思维能力，又可以使学生形成良好的解题习惯.

（四）利用分类讨论思想理解抽象概念

在初中数学教学中，抽象概念的掌握是提高学生解题质量的关键.但是，有很多学生在掌握概念的时候，经常会出现思维混乱的现象，尤其是对于一些相似性概念.因此，为培养学生的数学抽象素养，教师在教学数学概念的时候，可以通过分类讨论思想进行有机渗透，在分条件、分性质的过程中，帮助学生理解、判断，从而使其加深学习印象.

例如，对于“全等三角形”“相似三角形”的知识，由于概念掌握得不扎实，在运用它们解决问题的时候，很容易出现分辨不清、概念乱用的现象.为此，在解析概念的时候，可以引导学生从全等三角形和相似三角形定义、分类开始分析，先让学生根据题意所涉及的图形是什么三角形，然后根据区分点引导其进行讨论.

通过分类讨论交流，在思维碰撞的基础上，就全等三角形和相似三角形抽象概念进行解析，最后为学生设计有关全等三角形或者相似三角形的习题，让学生根据所掌握的概念，进行分类讨论交流，提高概念理解能力和应用能力.

结 语

分类讨论思想在初中数学教学中的应用，不仅可以提高学生的数学学习能力，还可以促进其思维发展，培养其思维灵活性和系统性，对提高学生问题解决能力和数学学习能力具有重要的意义.为此，在教学中，教师一定要重视分类讨论思想的应用.通过将分类讨论思想与函数、方程、动点问题、抽象概念的有机整合，学生掌握了数学分类讨论思想，并学会运用分类讨论思想解决数学问题，从而提高数学学习效果.

【参考文献】

[1]邱琴.分类讨论思想在初中数学教学中的应用分析[J].当代家庭教育，2020（32）：96-97.

[2]王李杰.分类讨论思想在初中数学解题中的应用研究[J].中学生数理化（教与学），2020（10）：45.

[3]梁静静.分类讨论思想在初中数学解题教学中的运用探析[J].数理化解题研究，2020（29）：20-21.

[4]郑雪梅.分类讨论思想在初中数学教学中的应用[J].新课程，2020（36）：150.