基于灵敏度的六自由度并联机构误差分配方法

谭 爽，梁凤超，陈 龙，林 喆，康建兵

（北京空间机电研究所，北京 100090）

0 引言

由于受到发射力学环境、在轨重力场和温度场等因素的影响，空间光学载荷系统入轨后部组件易产生相对位姿失配和面形误差，导致光学载荷的探测性能偏离原有设计、系统探测性能和成像质量严重衰减［1-2］。对于传统中小口径光学载荷系统，通常采用先进的热控、轻量化、桁架、重力卸载等技术手段，弱化入轨后重力场和温度场变化所造成的影响，从而保证光学系统的探测性能和成像质量［3-5］。而对于大口径高性能光学载荷系统，其部组件尺寸更大，受热力场与重力场变化的影响更敏感，探测性能和成像质量对部组件位姿及面形精度的要求更加精确，传统的轻量化、无热化等被动技术手段已无法满足大口径高性能光学载荷的宇航工程需求。针对这一工程难点，国外已采用主动光学与自适应光学的方法，在光学载荷系统中增加精密主动调整控制装置，在轨矫正部组件的相对位姿失配与面形误差，确保大口径高性能光学载荷在轨运行时的探测性能和成像质量［6-8］。在工程实现方面，国外主要采用六自由度并联机构作为次镜或拼接主镜的位姿调整机构［9-11］。六自由度并联机构有精度高，刚度大，动态性能好和摩擦小等优点［12-14］。

大口径光学载荷系统对六自由度并联机构的精度要求可达到亚微米级与角秒级，对六自由度并联机构精度指标较为严格，因此在设计时必须进行精度分析与误差分配［15-16］。精度分析是根据六自由度并联机构各组成部件的加工误差和安装误差，分析它们对六自由度并联机构位姿误差的影响，修改相关误差参数，以达到期望的精度指标。误差分配是根据并联机构位姿精度指标的要求，反求应分配给各组成部件的制造误差和安装误差，并使其达到一定的均衡。

在并联机床的精度分析领域，已经有一些学者进行了探讨，但在精度综合领域，目前研究还较少。在误差综合中，由于位姿误差与铰点误差关系高度非线性与强耦合，在给出精度指标要求时，无法利用误差模型直接求出铰点误差。卢强等［17］利用蒙特卡洛法，综合考虑零部件制造公差和运动副配合间隙误差，对六腿并联机床进行了精度综合。该方法具有过程清晰、编程简单的优点，但Monte Carlo方法计算精度的可靠性体现在样本点的容量，对一个位姿，样本容量为（10～100）×104，如果在全工作空间内进行位姿精度分析，其计算量巨大，难以实现。赵永杰等［18］运用误差独力作用原理和原始误差等效原则，将误差模型线性化，进行误差综合，使并联机器人精度综合变得简单可行，但是忽略了模型的耦合性。赵新华等［19］以6-SPS并联机器人机构为例，在结构误差敏感方向建立了杆长误差与位姿误差之间的解析关系，得出误差影响系数，该方法在某一位姿时只需要计算一个方程组，就能够实现精确、定量的误差分析，但没有考虑铰点位置误差关系，无法为铰点安装与制作提供指导依据。

本文建立六自由度并联机构误差模型，并利用误差模型定义铰点误差的灵敏度，给出位姿误差一定时铰链铰点位置误差分配方法，避免了大量运算。该方法简单高效，适用于六自由度并联机构铰点误差分析。

1 理论基础

Stewart平台是典型的六自由度并联机构，本文研究的是如图1 所示的6-UCU并联机构：该机构上下平台以6 个分支相连，每个分支两端是两个胡克铰，中间是一圆柱副。驱动器推动圆柱副作相对移动，改变各杆的长度，使上平台变化在空间的位置和姿态。

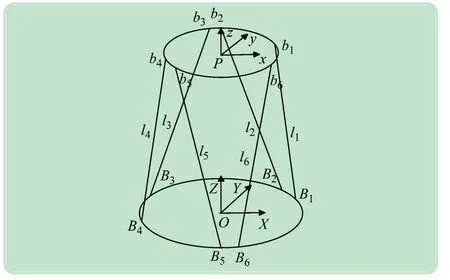
图1 6-UCU型Stewart并联机构

上下平台各个铰链点分别记作bi和Bi（i=1，2，…，6），分布为：bi分布在半径为r的圆上，且b1、b3、b5和b2、b4、b6分别构成2 个正三角形，其相对夹角为α，如图2（a）所示；Bi分布在半径为R的圆上，且B1、B3、B5和B2、B4、B6分别构成2 个正三角形，其相对夹角为β，如图2（b）所示。零位姿时上下铰点所在平面之间的距离为六自由度并联机构的高度H，杆长记为L0。r、α、R、β和H决定了六自由度并联机构的构型，为结构参数。

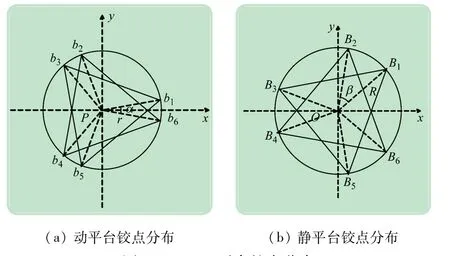
图2 Stewart平台铰点分布

并联机构常用的误差模型在只考虑几何误差的情况下，非几何误差因素对并联机构运动精度的影响较小，于是在建立Stewart六自由度并联机构的误差模型时可忽略非几何误差因素，只考虑安装误差、制造误差和杆长误差等系统误差。系统误差考虑以下几点：

（1）安装误差。对Stewart并联机构而言，固定在动平台与静平台上的铰链安装误差参数共有36 个独立参数。

（2）制造误差。铰链本身受加工精度和安装精度的限制，其回转轴线间并不可能理想的垂直，运动中心不可能重合于一点，这些都影响着铰链的运动精度。

（3）杆长误差。驱动支链杆在加工过程中受到加工精度的影响，其初始长度也会存在误差，一共6 个独立的长度误差参数dli（i=1，2，…，6）。

铰链的安装误差和制造误差最终造成铰链旋转铰点有位置偏差，即铰点位置误差，一共有36 个：dcj（Δxbi，Δybi，Δzbi和ΔxBi，ΔyBi，ΔzBi）（i=1，2，…，6，j=1，2，…，12）。因此，对于一般的Stewart 平台，为了减小标定模型的复杂性，在进行误差建模的过程中只考虑铰点误差和杆长误差共计42 项独立的机构参数误差，并进行误差数学建模。

对上平台进行欧拉旋转：①首先绕动坐标系z 轴转动Ψ；②然后绕动坐标系y 轴转动φ；③最后绕动坐标系x轴转动θ。

由上平台向惯性参考坐标系投影，可得表示上平台姿态的方向余弦阵为

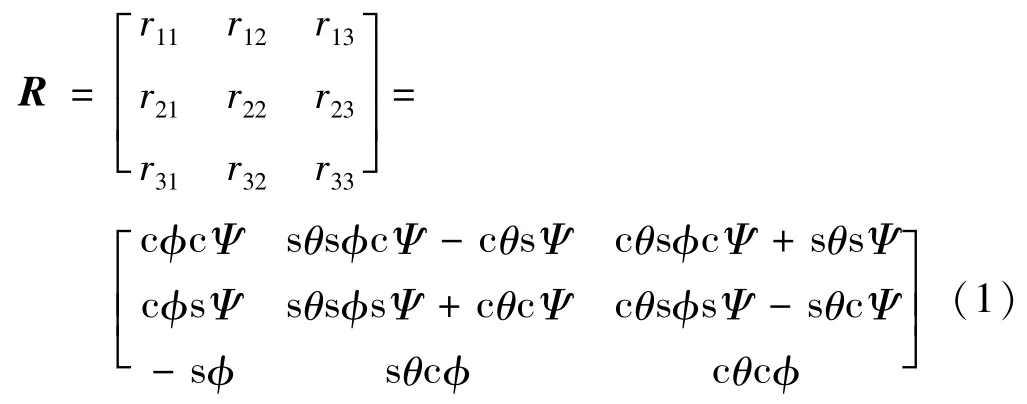
式中：

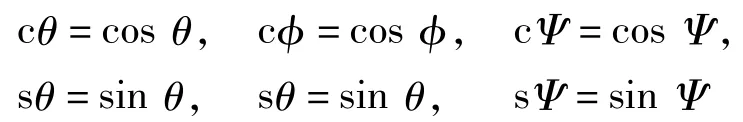
当给定机构的各个结构尺寸和动平台的位姿后，可确定动平台铰链点在动坐标系中的坐标Pbi，再通过旋转矩阵的变换可求出动平台铰链点在静坐标系中的位置qbi，即

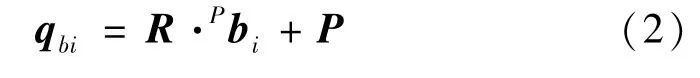
这时，支杆杆长矢量li可在固定坐标系中表示为

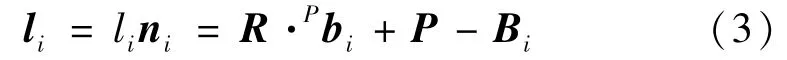
式中：li为第i个支杆的杆长；ni为第i 个支杆的单位向量；Bi为静平台铰第i个铰点在静坐标系中的坐标。

对式（3）进行全微分，得：

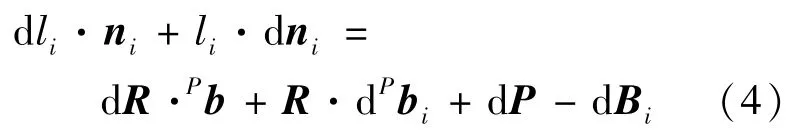
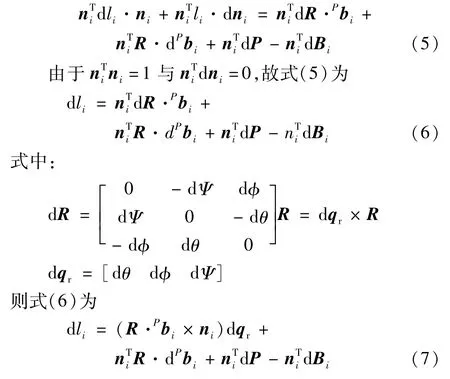
综合6 个驱动支杆，式（7）整理成矩阵形式，可得：

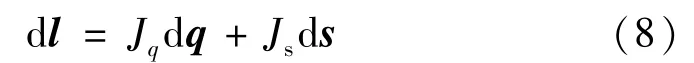
式中：

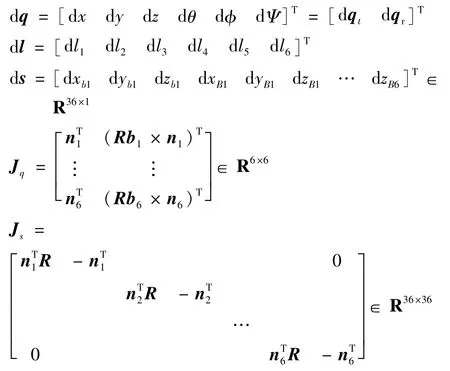
将式（8）整理成六自由度并联机构的误差模型：

式中，

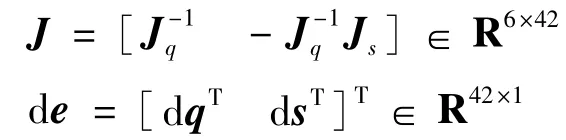
dq为动平台位姿误差矢量；dl 为6 个支杆的杆长误差；ds为动、静平台铰链的铰点位置误差；de是包含dl与ds 42 项独立的机构参数误差；J是六自由度并联机构结构参数存在误差情况下的误差传递矩阵，即误差传递雅克比矩阵。

2 铰点误差分配方法

考虑到杆长误差可以在控制算法中补偿，因此为了简化误差分配的难度，在误差分配时只考虑铰点误差，即dl=［0 0 0 0 0 0］，代入式（9）可得：

因为Js不是方形矩阵，无法求逆，因此当已知六自由度并联机构位置与姿态误差时，无法根据式（10）的逆向运算求得铰点误差。为解决该问题，引入矩阵奇异值进行精度误差分析。

为了将六自由度并联机构每个铰点误差与机构的位置误差与姿态误差分别对应，令：

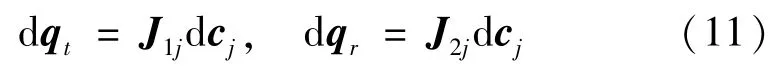
从式（11）可知，J1j与J2j分别为六自由度并联机构的第j个铰点对位置和姿态的误差传递矩阵，对J1j与J2j进行奇异值分解，分析误差传递特性，可以得到机构铰点误差和位姿误差的传递特性，即机构误差传递灵敏度评价指标。

以J1j为例，设铰点误差向量满足≤ρ，根据式（11）有

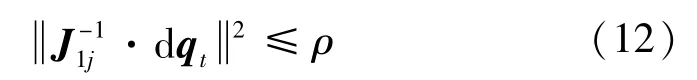
对误差传递矩阵F进行奇异值分解，得

式中：U=［u1，u2，…，um］和V=［v1，v2，…，vm］分别是和的特征向量矩阵，且Σ=［diag（σ1，σ2，…，σm）0］，σi是J1j的奇异值项（σ1≥σ2≥…≥σm≥0）。则J1j的逆矩阵为

式中

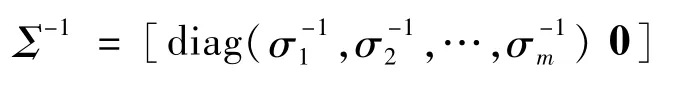
将式（14）代入式（12）有：

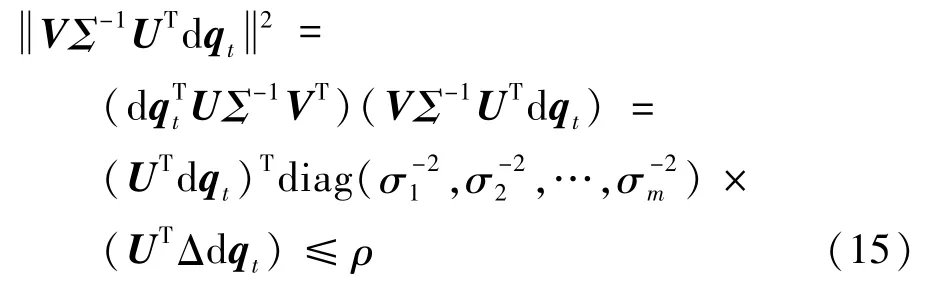
定义J1j和J2j矩阵的奇异值最大值为并联机构铰链铰点灵敏度（EAF），

当铰点位置误差一定时，灵敏度值越大，对应的机构位姿误差也就越大，机构位姿精度就越低；反之，当位姿误差一定时，灵敏度值越大，铰点位置误差值也就越小，即铰点精度就越高。

对于六自由度并联机构，当位姿误差为dq 时，可得铰点位置误差dcj应满足：

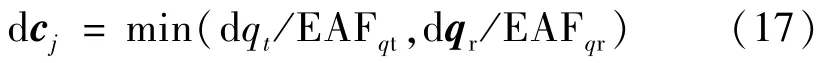
式中

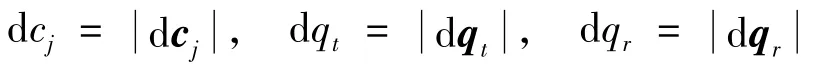
在复合运动不同位姿中，对每一个误差传递矩阵，先根据式（16）计算每个铰点在相应位姿时的EAF，再取整个过程中每个铰点对应的EFA最大值，为整个运动过程中该铰点的EAF。最后根据式（17）可求出每个铰点的位置误差，用来指导铰链的加工与安装。

3 某型号六自由度并联机构的铰链铰点误差分析

对于某空间光学遥感系统中六自由度并联机构精度要求为平移精度2 μm，旋转精度2″，即19.39 μrad，结构参数如下：r=239.51 mm，R=249 mm，H=195.03 mm，α=0.23 rad，β=0.268 rad。

为能够计算出各个铰点的EFA，需要让上平台运动到所有要求的六维工作空间。为简化计算量，给定上平台低频平移自由度运动规律与高频转角自由度运动规律的复合运动，如表1 所示。以此为仿真规律，仿真总时间为60 s。

表1 复合运动仿真规律

在复合运动中，以时间0.1 s为步距，在MATLAB中编程，计算每个铰点在所有位姿下的灵敏度EAF值，如图3 所示。由图可以看出，不同位姿对应的灵敏度是不一样的。但灵敏度数值不会相差过大，始终在一个数量级上。取最大值为在该复合运动中铰点的EAF，如表2 所示。

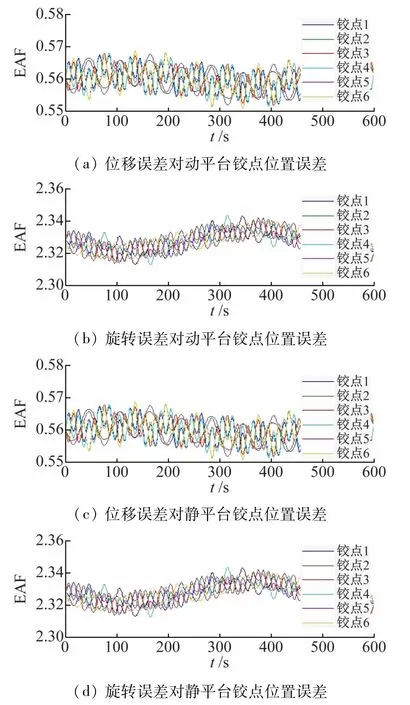
图3 位姿位差对铰链铰点误差的灵敏度

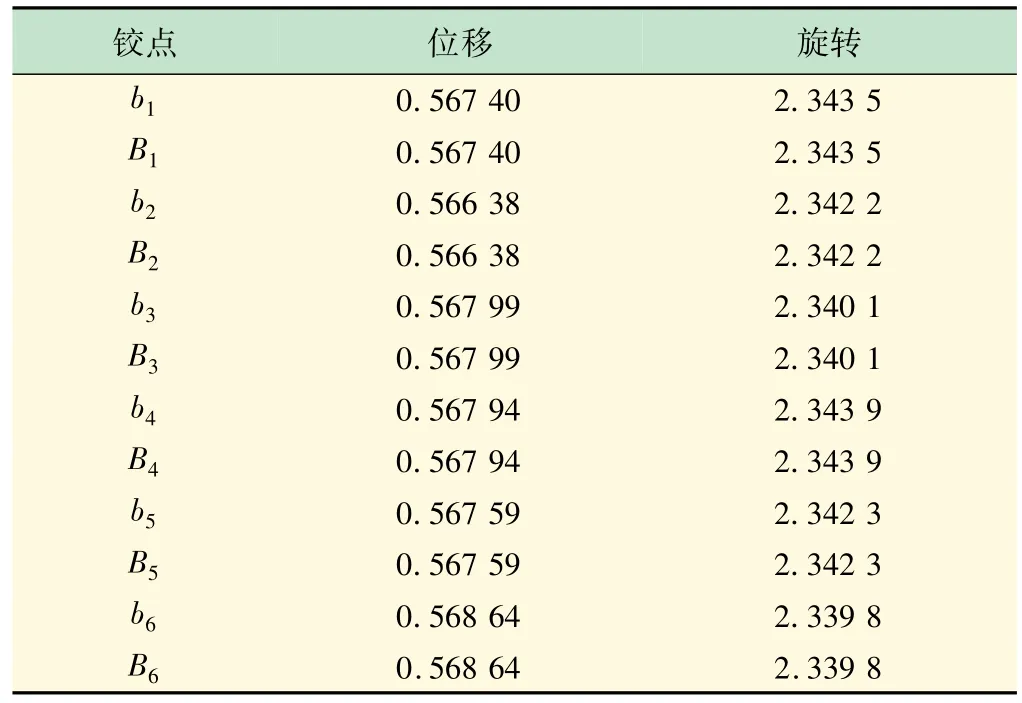
表2 运动范围内不同铰点对应的EAF

当给出位姿误差（即动平台运动精度）时，先合理分配位姿误差，这里考虑工作范围内，铰点误差的占比是一样的，均匀分配给每个铰点，则对于铰点b1，有dqt_b1=dqt/12dqr_b1=dqr/12，其位置误差在半径为dqt_b1的包络球内，姿态误差在半径为dqr_b1的包络球内。根据式（16）可以求出铰点b1位置误差：

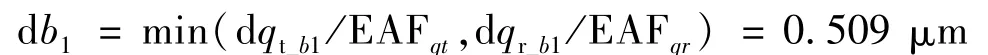
对铰点b1，其位置误差应该在半径为0.508 μm 的包络球内。

同理可求出每个铰点的位置误差，如表3 所示，可以知道每个铰链在加工与安装过程中造成的铰点位置误差应该在某个包络尺寸内。

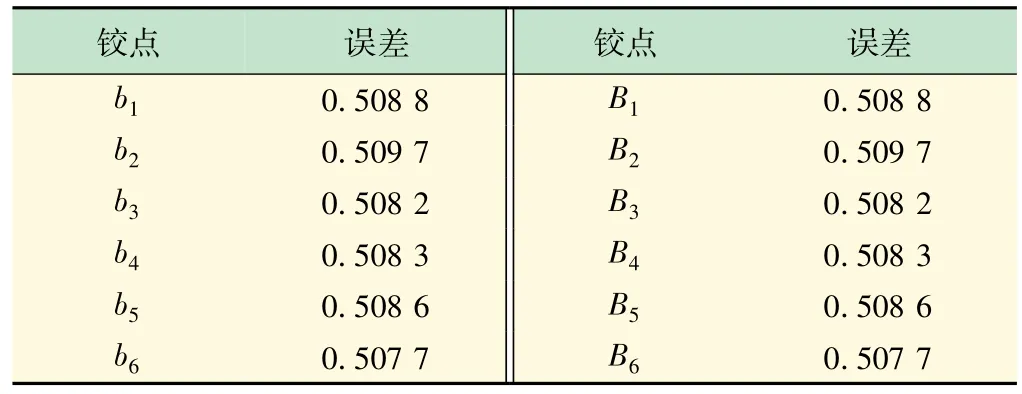
表3 铰链铰点位置误差

可以得到，每个铰点的位置误差在同个数量级，相差在0.39%以内。在实际应用过程中，可以选取任意铰链铰点进行计算分析。

4 结语

对于高精度六自由度并联机构，铰链的加工安装误差至关重要。然而位姿误差与铰链铰点误差关系具有非线性强耦合多变量等特点，在给定六自由度并联机构的六个位姿误差时，无法直接求解出36 个铰点误差。文章基于灵敏度提供了一种铰点误差分配方法。该方法计算过程清晰，相对简单，计算量小，在高精度六自由度并联机构的铰链加工与安装中给出精度指导与依据。