剪力钉倾斜对其力学性能影响分析

张柳煜,金 鑫,苏 举,孙武云,黄乐州

(1.长安大学桥梁与隧道陕西省重点实验室，长安大学，陕西 西安 710064；2.中设设计集团股份有限公司，江苏 南京 210014；3.云南武倘寻高速公路有限责任公司，云南 昆明 650000)

钢-混组合结构桥梁是将钢梁与混凝土桥面板通过抗剪连接件连接成整体共同受力的桥梁形式，剪力钉是钢混组合结构中非常重要的连接构件，起到了抵抗钢梁与混凝土之间的纵向剪力和防止钢板与混凝土板掀起的作用，但由于构件在加工，制作以及安装的过程中存在的问题，剪力钉连接件往往会出现尺寸偏差、剪力钉空洞、剪力钉倾斜等误差，这些误差往往对其力学性能产生较大的影响。

目前国内外对于剪力钉受力特性的研究主要通过拉拔及推出实验来获取剪力钉的极限抗拉拔及抗剪承载力，对剪力钉的相关规范也是通过实验为基础。20世纪50～60年代，美国工程师就对钢-混组合梁和剪力连接件进行了实验研究[1-2]；90年代，Deric J.Oehlers[3]对在疲劳荷载作用下，剪力钉的荷载滑移曲线和其应力应变关系进行了实验和理论研究，为之后剪力钉破坏机理的研究奠定了基础；2000年胡夏闽[4]等人对剪力钉抗剪承载能力计算公式展开了研究，给出了基于可靠度的剪力钉承载能力计算公式；2007年周伟翔[5]为了验证剪力钉抗剪承载能力计算公式的准确性，将剪力钉连接件推出实验模型所得结果与理论结果就进行了对比研究；2015年蔺钊飞[6-7]等人建立室内缩尺推出模型试验，得出了可以防止钢-混组合梁脆性破坏的有效措施，即控制剪力连接件的高径比，控制混凝土的强度等；2017年李成君[8]等人设计了装配式剪力钉的布置方式，通过推出试验对剪力钉的滑移性能进行研究，为组合梁剪力钉设计提供了参考；2018年甘屹东[9]等人进行静力推出试验，研究钢与超高性能混凝土之间焊接抗剪连接件的抗剪性能，并结合工程背景研究了布置方式对其的影响。

本文首先通过通用有限元分析软件abaqus，选用合理的参数，来模拟剪力钉连接件的拉拔及推出实验，并与相关文献中的实验结果进行对比，来验证本文所采用的材料本构关系、参数取值及有限元模拟方法的可靠性和精确性，然后以有限元分析为基础，建立不同的工况，研究剪力钉倾斜对其力学性能的影响，为制定剪力钉的的设计和施工误差控制范围提供了参考。

1 有限元模型建立

本文通过通用有限元软件ABAQUS建立仿真模型，采用C3D8R实体单元，混凝土材料参数如下：Ec为34 500 MPa,Fck为32.4 MPa，Ftk为2.64 MPa，ν为0.2，混凝土本构采用ABAQUS损伤塑性模型[10]。混凝土拉压应力-应变关系如图1、图2所示。

图1 混凝土受拉应力-应变关系

图2 混凝土受压应力-应变关系

剪力钉的本构模型选用双折线模型，不考虑刚度退化[11，12]，材料强度根据试验结果选取[3]，其余相关参数依据《公路钢结构桥梁设计规范》[13]选取，见表1。

表1 材料参数Table1 MaterialparametersE/GPafy/MPafu/MPaν剪力钉2064205190.31钢梁2063450.31钢筋2064000.31

有限元模型及网格划分见图3，剪力钉与其周围相接触的混凝土采用硬接触，并进行了网格加密处理，以提高计算精度。有限元计算中，忽略了混凝土与钢板之间的切向摩擦力，仅考虑法向的相互作用。

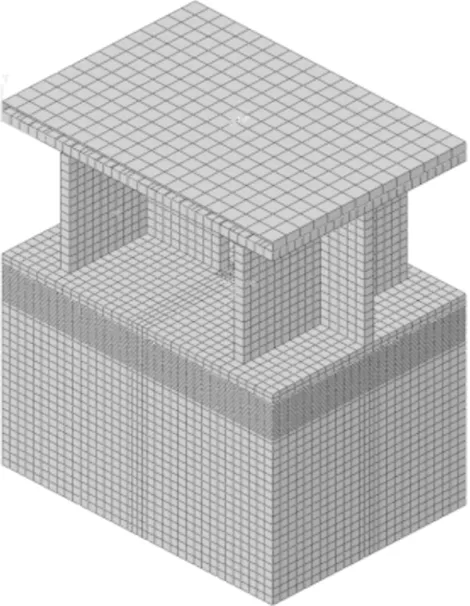
图3 剪力钉试验数值分析模型

2 剪力钉模型验证

2.1 剪力钉连接件拉拔试验模型的验证

本文选择直径为22 mm，长度为100 mm(以下简称Φ22×100)剪力钉模型，及直径为22 mm，长度为300 mm(以下简称Φ22×300)剪力钉模型进行拉拔试验有限元模拟，绘制以剥离量为横坐标，荷载大小为纵坐标的荷载剥离曲线，分析剪力钉的抗拉拔性能，并将模拟结果与周伟翔[5]进行的剪力钉拉拔实验结果进行对比。剪力钉拔出试验试件尺寸见图4。

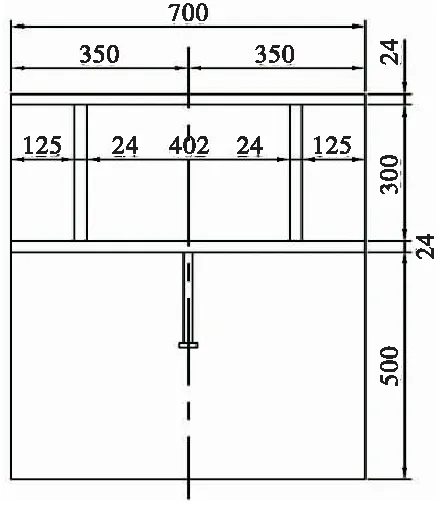
(a)立面图

Φ22×100剪力钉试件及Φ22×300剪力钉试件有限元模拟剪力钉荷载-剥离曲线与文献[3]对比结果如图5、图6所示。

图5 Φ22×100剪力钉荷载-剥离曲线

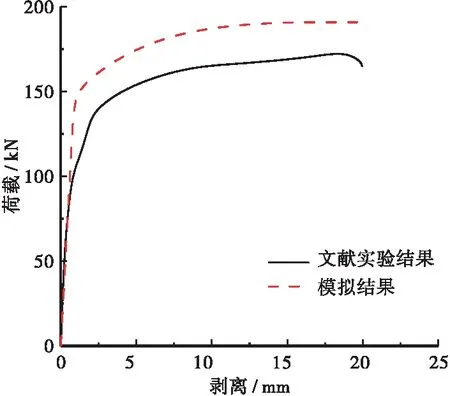
图6 Φ22×300剪力钉荷载-剥离曲线

由图5可知，在弹性阶段，Φ22×100剪力钉有限元模拟的结果与试件结果曲线变化趋势基本一致，抗剪刚度随着荷载的增加而逐渐减小，仿真结果较试验结果先进入塑性阶段，在文献试验中，剪力钉极限抗拉拔承载力为155.3 kN，而仿真结果仅比试验结果大4.1%。

由图7可知，在弹性阶段，Φ22×300 剪力钉有限元模拟的结果与试件结果曲线变化趋势基本一致，其破坏形式为剪力钉被拉断破坏，但由于在试验的过程中，很难对试件进行轴心受拉，实际试件会受到拉弯作用，因此有限元模拟的剪力钉抗拉极限承载能力比试验结果要略大。

用有限元模拟的剪力钉拉拔试验荷载-剥离曲线能较好地反映剪力钉的拉拔与破坏过程，与试验结果曲线相比，整体的发展规律相近，证明了有限元模拟结果是可取的，因此下文以该拉拔试验有限元模拟为基础，分析剪力钉倾斜对其抗拉拔性能的影响。

2.2 剪力钉连接件推出试验模型的验证

本文在封博文[14]等人静载推出试验的基础上，选择Φ22×300剪力钉试验模型进行推出试验有限元模拟，对剪力钉抗剪性能进行有限元分析。图7为仿真模型的尺寸图，剪力钉荷载-滑移曲线对比结果如图8所示。

2.2 3组术前、术后血红蛋白的比较 A、B、C 3组血红蛋白术后各时点均较术前明显升高，3组间术后3个月随访血红蛋白差异无统计学意义(P>0.05)，术后6、12个月B、C组血红蛋白明显高于A组，3组间差异有统计学意义(P<0.05)。见表3。

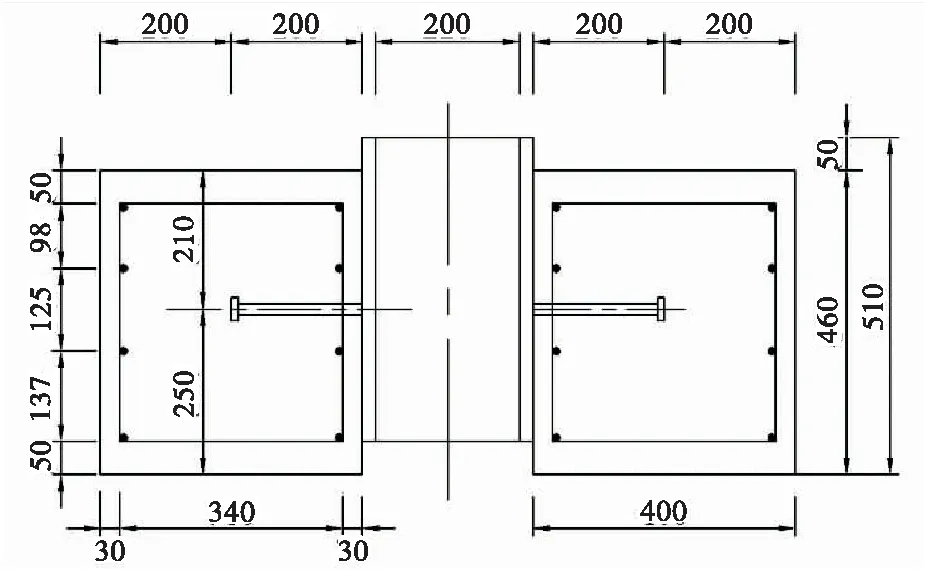
(a)立面图

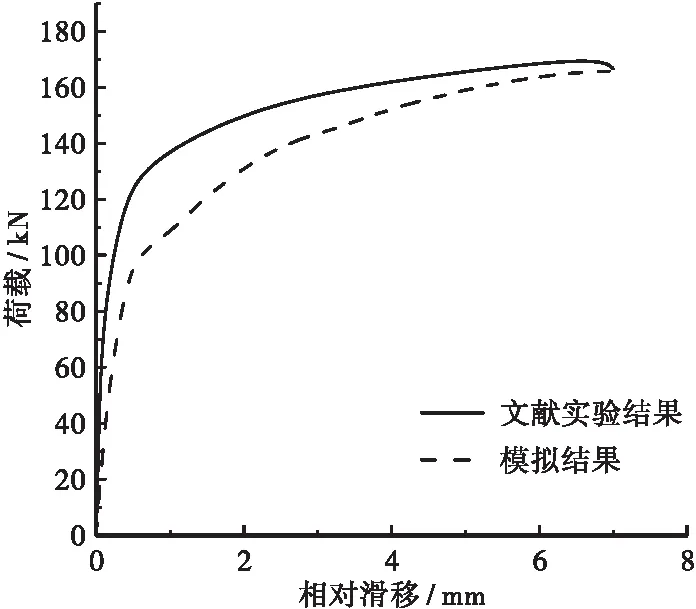
图8 Φ22×200剪力钉荷载-滑移曲线

由图8可得，有限元模拟的结果与试验结果变化趋势基本一致，二者极限抗剪承载力相对误差仅有3.3%，相对滑移量也相差不大，说明有限元模拟的结果较为准确，下文以该有限元模拟为基础，分析剪力钉倾斜对其抗剪性能的影响。

3 剪力钉倾斜对拉拔性能的影响

剪力钉在施工、焊接以及拼装的过程中，不可避免会产生一定的倾斜，本文运用单因素敏感性分析法，分不同工况，针对不同倾斜角度，通过有限元模拟剪力钉的拔出试验，研究剪力钉倾斜对其拉拔性能的影响。仿真模拟采用C50混凝土，直径22 mm，长度150 mm的Φ22×150剪力钉。各工况倾斜角度有：工况1为0°，工况2为5°，工况3为10°，工况4为20°，工况5为30°，工况6为40°，工况7为50°。不同倾角的剪力钉剥离量曲线如图9所示、不同倾角的剪力钉荷载-剥离曲线如图10所示、不同倾角的剪力钉极限抗拔承载力变化曲线如图11所示。

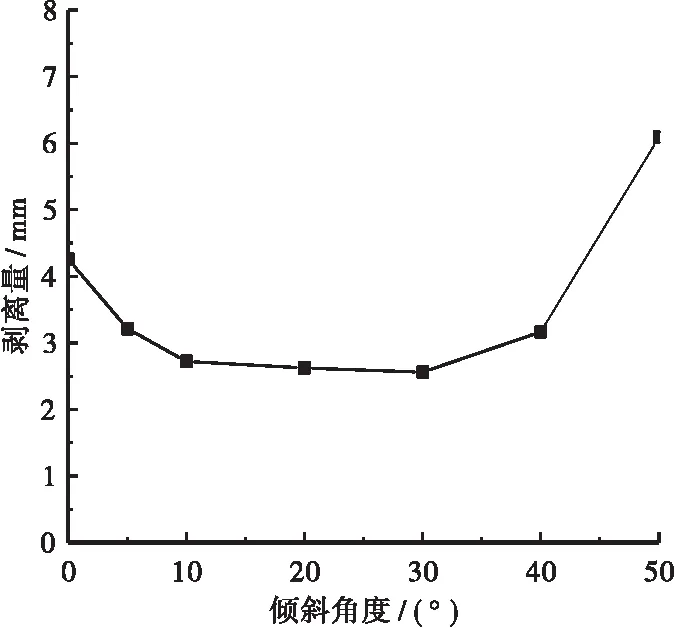
图9 不同倾角剪力钉剥离量曲线

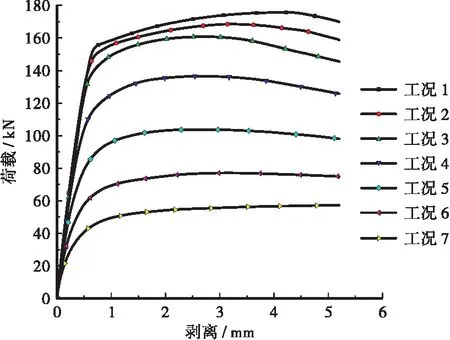
图10 不同倾角剪力钉荷载-剥离曲线

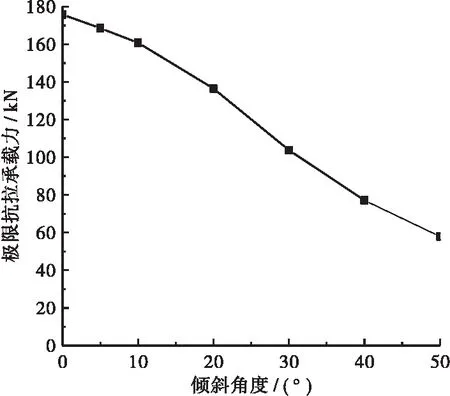
图11 不同倾角剪力钉极限抗拔承载力曲线

由图9可得，剪力钉剥离量随着倾斜角度的增大先增大后减小，从0°～5°降低的最快，30°时降低到谷值。倾斜角度为5°～40°时，其剥离量分别降低了24.5%，36.0%，38.4%，39.9%，25.6%，倾斜角度为50°时，剥离量增高了43.1%。

由图10可得，不同倾斜角度剪力钉荷载剥离曲线的发展趋势一样，随着倾斜角度的增大，同一剥离量对应的荷载大小减小，因此倾斜角度的不同仅对剪力钉极限抗拉承载力和对应的剥离量有影响。

由图11可得，随着剪力钉倾斜角度的增大，其极限抗拉拔承载力不断下降，且下降幅度越来越大，当倾斜角度为50°时，剪力钉的极限抗拉承载力降低了70%，说明剪力钉的抗拔承载力对倾斜角度的变化较为敏感。

由有限元模拟结果可得，剪力钉倾斜时其拔出试验的破坏形态均为混凝土破坏。当剪力钉倾斜角度大于5°时，剪力钉的破坏形态为脆性破坏，无明显的塑性变形，对结构危害较大，应该避免。通过剪力钉抗拉承载力和和破坏模式对剪力钉倾斜角度的敏感程度分析可知，为了避免剪力钉抗拉拔承载能力大幅降低以及剪力钉的脆性破坏，在施工过程中应该将剪力钉的倾斜角度控制在5°以内。

4 剪力钉倾斜对抗剪性能的影响

为研究剪力钉倾斜对其抗剪性能的影响，本文分不同工况，针对不同的推出方式(顺推：使得剪力钉根部混凝土受压区增大；逆推：使得剪力钉根部混凝土受压区减小)，通过有限元模拟减小不同倾斜角度的剪力钉推出试验。仿真模拟采用C50混凝土，Φ22×200剪力钉。工况编号见表2。顺推时剪力钉抗剪荷载滑移曲线见图12，逆推时剪力钉抗剪荷载滑移曲线见图13，抗剪承载力变化曲线和对应滑移量变化曲线见图14、图15所示。

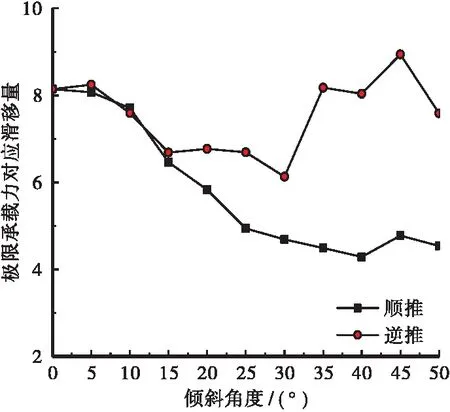
图15 滑移量随倾斜角度变化折线图

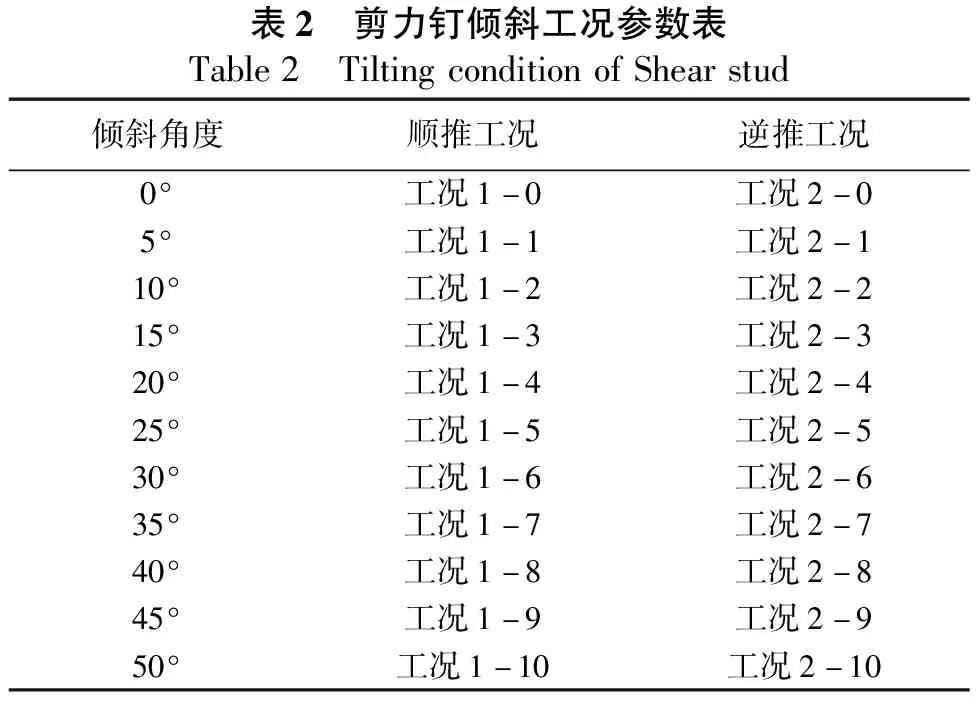
表2 剪力钉倾斜工况参数表Table2 TiltingconditionofShearstud倾斜角度顺推工况逆推工况0°工况1-0工况2-05°工况1-1工况2-110°工况1-2工况2-215°工况1-3工况2-320°工况1-4工况2-425°工况1-5工况2-530°工况1-6工况2-635°工况1-7工况2-740°工况1-8工况2-845°工况1-9工况2-950°工况1-10工况2-10

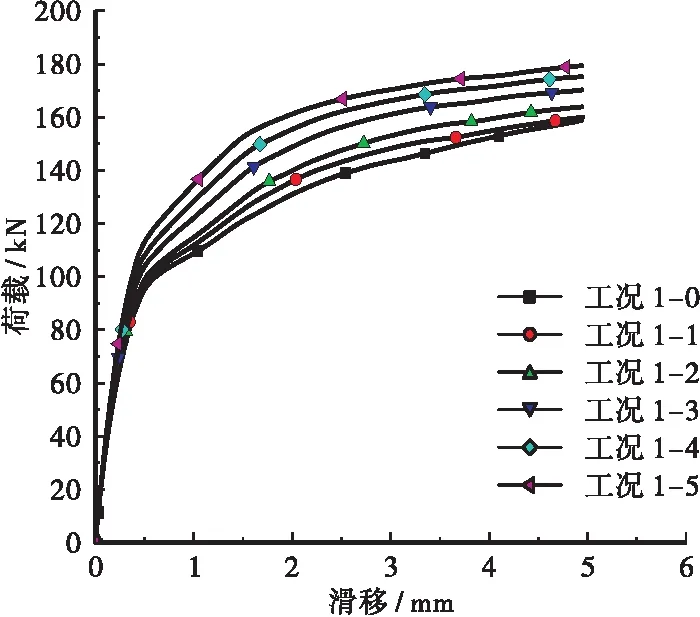
图12 顺推剪力钉荷载-滑移曲线

由图12、图13可知，随着倾斜角度和推出方式的变化，剪力钉的荷载滑移曲线的发展趋势变化不大，但是剪力钉极限抗剪承载力和对应的截面滑移量大小对倾斜角度的变化较敏感。

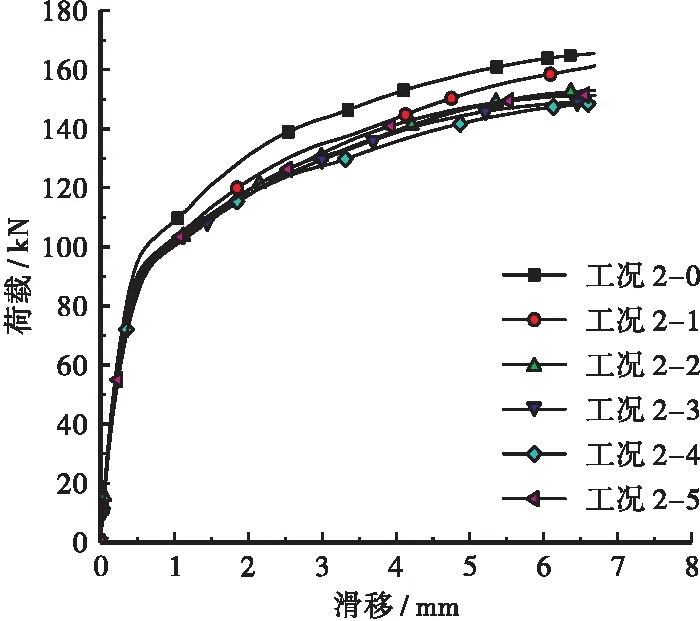
图13 逆推剪力剪荷载-滑移曲线

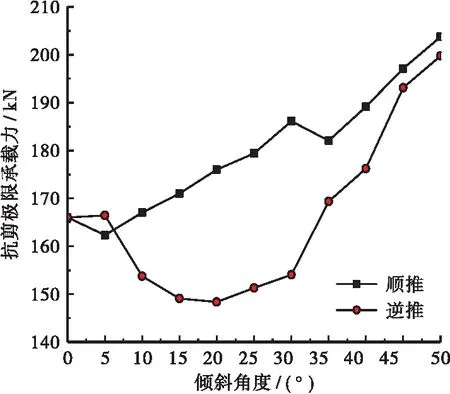
图14 抗剪承载力随倾斜角度变化折线图

逆推时，剪力钉抗剪极限承载能力大体随着倾斜角度的增加先减小后增大。当倾斜角度为5°时，略有增加，相较于垂直状态增加了0.2%；当倾斜角度为20°时，剪力钉极限抗剪承载能力最小，相较于垂直状态，降低了10.6%。由图10可知，当剪力钉的倾斜角度控制10°以上时，顺推相较于逆推更有利。

由图15可知：对于顺推，剪力钉极限抗剪承载力对应滑移量大体随着倾斜角度的增加而减小，5°～25°之间，降低的速度最快，25°之后，降速变缓，滑移量也逐渐收敛。到40°时，剪力钉抗剪承载力最低，相比于垂直状态降低了47%。对于逆推，界面滑移量变化趋势较复杂，变化幅度较小，剪力钉极限抗剪承载力对应滑移量大体随着倾斜角度的增加先减小后增大。

不同倾斜角度和不同推出方向下，剪力钉的受力形态和破坏模式不同，因此剪力钉的极限抗剪承载能力和对应的滑移量会呈现上述的规律。表3给出了不同倾斜角度和不同推出方向的剪力钉的破坏形态。

表3 结构破坏形态Table3 Structuralfailurepatterns倾斜角度顺推逆推 0°剪力钉剪断剪力钉剪断 5°剪力钉剪断剪力钉剪断10°剪力钉剪断混凝土压碎15°剪力钉剪断混凝土压碎20°剪力钉剪断混凝土压碎25°剪力钉剪断混凝土压碎30°剪力钉剪断混凝土压碎35°剪力钉剪断混凝土压碎40°剪力钉剪断混凝土压碎45°剪力钉剪断剪力钉剪断50°剪力钉剪断剪力钉剪断

当剪力钉垂直状态时，剪力钉的破坏形态为剪力钉根部被剪断破坏，其抗剪承载力主要由材料的抗拉强度和剪力钉的截面积控制，顺推时，当剪力钉发生倾斜，与剪力钉接触的混凝土的受压区域面积增大，对于剪力钉的抗剪是有利的，因此，剪力钉倾斜会增加剪力钉的抗剪承载力，但是剪力钉一旦发生倾斜，在抗剪的同时，也将承担更大的轴向拉力，因此剪力钉的塑性状态来的更早，破坏也提前。

逆推时，剪力钉根部接触的混凝土受压区域会因为剪力钉的倾斜角度增大而减小，这对于剪力钉抗剪是不利的，但当倾斜角度较小时(5°左右)，剪力钉的抗剪承载力主要还是受材料的抗拉强度和剪力钉的截面积控制，其抗剪承载力降低程度不大，破坏形式依旧为剪力钉剪断破坏；当倾斜角度不断增大(20°左右)，此时混凝土的受压区域不断减小，对剪力钉的抗剪影响较大，破坏形式也变为混凝土压碎破坏；当倾斜角度继续增大时，剪力钉所受的轴向压力不断增大，与剪力钉根部接触的混凝土所受的压力不断减小，一定程度上提高了剪力钉抗剪承载力，此时破坏形态变为剪力钉剪断破坏。

剪力钉的倾斜角度对剪力钉抗剪承载力以及破坏形态影响影响较大，在施工中因充分考虑剪力钉倾斜角度的误差。由上述分析可知，当剪力钉倾斜角度在5°以内时，剪力钉抗剪承载力变化较小，且剪力钉破坏形态也没有改变，因此从抗剪性能角度出发，在施工过程中应将剪力钉的倾斜角度控制在5°以内。

5 结论

a.通过ABAQUS软件能较为精确地模拟出剪力钉的抗拉拔实验以及抗推出实验。

b.拉拔实验模型中，随着倾斜角度的增大，剪力钉的抗拉拔承载力逐渐减小，其对应剥离量先增大后减小，不同倾斜角度的剪力钉拔出实验破坏形态均为混凝土破坏。

c.推出实验模型中，顺推时，剪力钉倾斜会使混凝土受压区域增大，有利于剪力钉抗剪。随着倾斜角度的增大，剪力钉变化的大体趋势是极限抗剪承载力增大，对应的滑移量减小。

d.逆推时，剪力钉倾斜会减小混凝土的受压，这对于剪力钉抗剪是不利的。随着倾斜角度的增加，剪力钉破坏形态从剪力钉剪断破坏变为混凝土压碎破坏再变为剪力钉剪断破坏，极限抗剪承载力和对应滑移量的大体变化趋势为先略微增加后减小再增加。

e.由剪力钉倾斜对其抗拔承载能力以及抗剪承载能力的影响，建议施工过程中将剪力钉倾斜角度的误差控制在5°以内。