区间直觉模糊数排序指标的对比分析

牛利利

（广西大学行健文理学院，广西 南宁 530004）

区间直觉模糊集的概念最早是由Atanassov和Gargov[1]提出的，由于其在反映事物的不确定性方面更加精确，排序区间直觉模糊数的方法也成为学者研究的主题。文献[2]探讨了区间直觉模糊数的距离公式，在此基础上提出了基于TOPSIS的区间直觉模糊决策方法。文献[3]将排序直觉模糊集的方法推广到区间直觉模糊集中。文献[4]利用得分函数和精确函数排序区间直觉模糊数。文献[5-6]研究了排序区间直觉模糊的排序指标。本文在此基础上，结合文献[5-10]定义的得分函数等排序指标，将决策者的风险倾向考虑进得分函数，提出新的得分函数，通过与现有的排序区间直觉模糊数的排序指标进行对比，通过实例说明新排序指标的可行性和有效性。

1.区间直觉模糊集的定义

定义2.1[1]设为区间直觉模糊集，其中X是一个非空集合，为元素x属于的隶属度区间，为x属于的非隶属度区间，且

定义2.2[4]设为区间直觉模糊数，为区间直觉模糊数的犹豫区间，则

2.区间直觉模糊数得分函数

定义3.1[4]设为区间直觉模糊数，则

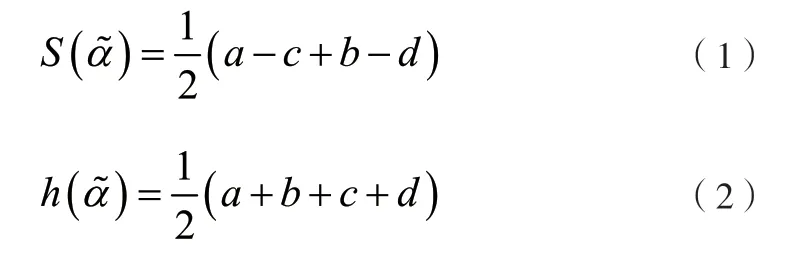
该方法从客观的角度来定义，忽视了决策者的主观意愿对决策结果的影响。一般情况下，决策结果会受决策者自身风险倾向的影响，本文将表达决策者意愿的参数考虑进得分函数，提出新的排序区间直觉模糊排序指标，如下：

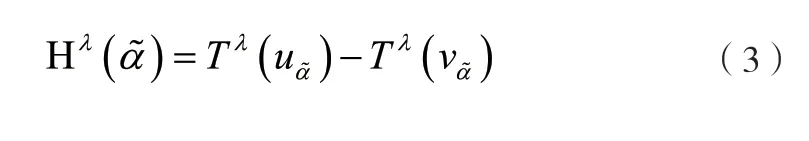
公式(4)进一步可化为

3.新得分函数与现有排序指标的对比分析

定义4.1[4]设为区间直觉模糊数，则

定义4.2[7]设为区间直觉模糊数，则

定义4.3[8]设为区间直觉模糊数，则

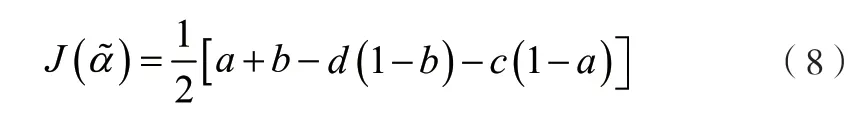
本文的排序指标得出的结果更符合实际情况。文献[4,7]的排序指标得属于中立型决策者的结果。文献[8]的排序指标得属于冒险型决策者的决策结果。

本文的排序指标得出的结果更符合实际情况。文献[4,7,8]的排序指标得属于中立型决策者的结果。本文的排序指标能够弥补文献[4,7,8]的排序指标无法排序的情况。

4.结语

本文对区间直觉模糊数的排序指标、运算法则和集成算子进行了介绍，由于现有的排序指标是从客观的角度定义的，忽视了决策者的主观态度对决策结果的影响，本文提出了反映决策者风险倾向的新得分函数，然后通过与现有的排序区间直觉模糊数的排序指标进行对比，通过实例对比分析，说明新排序指标的可行性和有效性。