活动的设计，需尊重儿童的经验

文∣于蓉

在小学教材中“分数”的概念一般表述为“把单位‘1’平均分成若干份，表示这样的一份或几份的数叫做分数”。小学数学教材编排有四个阶段，逐渐培养学生对分数的整体认识：认识平均分(二年级)，初步认识分数(三年级)，分数的意义(五年级)，分数与除法的关系及运用(六年级)。

“认识几分之一”是学生在三年级对数域的第一次扩展，既是初步认识分数的意义，也是在意义的基础上认识分数的计数单位，具有重要的意义。在实践中我们尝试从儿童的已有经验出发，尊重儿童的现实基础设计活动，感悟分数的内涵及其价值。

一、感受整体外延，丰富儿童视角

分数来自拉丁语，代表“破碎”，是整体的一部分，或任何数量相等的部分。在日常生活中，学生对部分和整体已有一些了解，如整体是由部分构成的，几个部分可以构成一个整体，但学生在观察现象时容易忽略整体。如，在一年级有“一图四式”的教学，学生常见的错误是忽略整体，用部分数量进行相减，出现“5-3=2、5-2=3”的错误(如图1)。分数教学中，表示涂色部分时，当图形的部分是均分时，总有学生认为可以用“四分之一”表示，忽略了应是整个图形作为一个整体的等分(如图2)。当涂色部分放在图形的中间时，也有学生用空白部分的份数作为分母，用三分之一表示涂色部分，忽略了分母应表示整个图形分的份数(如图3)。

图1

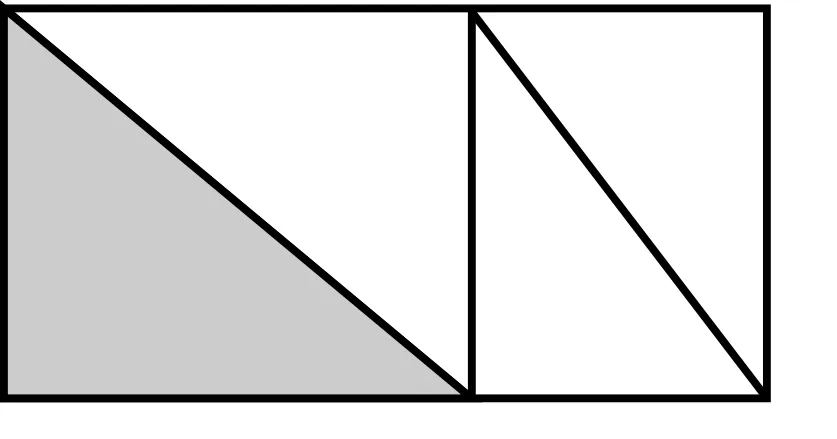
图2

图3

由此，我们需要将整体与部分作为分数教学的前奏。

【活动一】

师：在我们身边很多东西都是由部分和整体构成的。仔细看一看，说说哪个是部分，哪个是整体。

盘子和碎片

机器人和它的腿

师：在下面的图形中找一找，谁是部分，谁是整体。

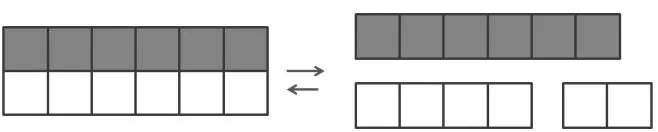
[教师引导学生]整体可以分成大小不同的部分，把部分合在一起就成为一个整体。

师：将其中的部分再分一分，你发现了什么？

[教师引导学生]部分还可以变成新的整体，整体还可以变成另外一个整体。

对整体和部分的理解，是学习四则运算必备的思维能力，也是学生认识分数意义的重要基础。在认识分数前再次回忆生活中的整体与部分经验，利用图形理解整体与部分的逻辑关系，感受整体能分成多个部分，而部分能重新构成整体，有时一个部分还可以作为一个新的整体，新的整体又可以分成几个部分。丰富学生观察的视角后再来研究分数，适合学生的年龄特点，可以唤醒学生已有经验，并会影响其在运用分数表达时自觉比较整体和部分的关系。

二、明晰“一半”内涵，丰富儿童经验

分数的产生起源于实际度量和物品均分。教材中一般从分一堆物体开始，分得的结果可以用整数表示；若平分一个物体，无法用整数表示，则出现了二分之一。从“分”开始，由二分之一再拓展到三分之一、四分之一，这样的安排遵循了分数的起源，符合了分数是“两个数的商”，也为分数概念的数学提供了路径。我们思考的是，将物体一分为二是分数的萌芽，学生对“一半”有丰富的生活经验，不仅能区分某个部分是否物体一半，也能分出一堆或一个物体的一半，但并未将一分为二、一半等口头语言进行分析、概括，并且符号化。教学中我们是否尝试从“一半”开始溯源，以学生对“一半”的已有经验为生长点，感悟分数的内涵。

【活动二】

1.认识一半

师：从小学到现在，同学们已经认识了很多数。你能用一个数表示下面物体的数量吗？(课件出示物体，学生报出数量)

师：可在生活中我们经常看到的不是一个整体，只是其中的一部分。现在你看到了什么？(出示图片)

生：都只是一半。

师：生活中的一半可真多呀！(出示小半个苹果)这是一半吗？为什么？

[总结]成为一个整体的一半是有要求的，必须是分成两个相等的部分，也就是要平均分。

2.找出图形的一半

师：请你找出一个圆形的一半并画连线表示。

学生动手操作。

教师为学生提供正方形、长方形、圆形、三角形。

3.学生交流，汇报

师：可以找到几个一半？为什么对折就可以找到圆形的一半呢？按序介绍不同图形的一半。

[学生思考]为什么这些一半的图形形状、颜色不一样，但都是它的一半呢?(只要图形分成2个相等的部分，一个部分就是它的一半)

4.用一个数来表示物体的一半

让学生自由发挥，用数表示物体的一半并解释缘由。

[教师引导学生]可以将1和2用起来，“平均分”加一条线来表示。

教师出示“二分之一”。

师：一块蛋糕平均分成两个部分，半块就是二分之一块。

[教师向学生解释]因为都表示把一个整体分成了两个相等的部分，一个部分就是它的一半，就是二分之一。

分数既有“量”也有“率”的含义，教师从学生熟悉的“一半”进行探究，首先感悟分数是一个数，可以表示具体的数量。在整数学习中，学生熟悉的是数作为量的含义， 从“一半”开始，可以直接明确“一半”是具体数量的表达，并在此基础上鼓励学生用数学符号表达数量，顺从学生的认知特点，易于学生理解分数作为一个“量”的意义。其次是感悟分数可以表达“率”。进入符号表达阶段，多样的“一半”中，不管大小、形状、属性和色彩等是否相同，都可以用“二分之一”表示，此时“二分之一”已经从具体的量中抽象出来，表示的是部分与整体之间的关系。从“一半”开始，到“一半”的表达，再到“一半”的符号化，“二分之一”自然地进入学生的视野，“分数”的内涵也在逐步渗透。

三、调整分数表达，契合儿童习惯

学生使用的言语可以让教师了解学生对数学的理解，但词语的运用还不能说明学生对概念的理解，有些只是简单的模仿。为便于学生理解、建立新的概念，教师需尽量减少使用学生陌生、模糊的词语。审视教材中“分数”的最终表达：“把单位1平均分成若干份，这样的一份或若干份可以用分数表示。”这样的表达有两个障碍，一是单位“1”，尽管教材是从一个整体、一些物体逐步推进分数的学习，再由一个物体、一个计量单位、一个整体概括得出单位“1”，但学生需花费大量时间理解这个新词语。二是“平均分”是在二年级除法学习中建立的概念，平均分含有“等分除”和“包含除”，丰富的内涵会让学生忽略其本质是等分。基于这两点考虑，教师教学设计如下。

【活动三】

师：下面的图形可以用怎样的分数表示呢？为什么？

教师引导学生说出理由，把一个整体分成了3个相等的部分时，其中的一部分可以用“三分之一”表示；把一个整体分成了5个相等的部分时，其中的一部分可以用“五分之一”表示；把一个整体分成了9个相等的部分时，其中的一部分可以用“九分之一”表示。

师追问：想象一下，还会有哪些分数呢？它们会是什么样子呢？

[总结]把一个整体分成了几个相等的部分时，其中的一部分可以用“几分之一”表示。

师：下面图形的涂色部分可以用“四分之一”表示吗？为什么？

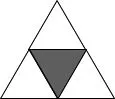
图1

图2

图3

师追问：图1为什么是四分之一？图2我们看到了3份，为什么不是三分之一？图3是4份，为什么不是四分之一？

[总结]要确定用几分之一来表示，我们要观察是把一个整体分成了几个相等的部分，每一部分就是它的几分之一。

这样安排教学有两个特点，一是直接用“整体”替代“一个物体”，一个物体、一堆物体都可以看作整体，无须用其他词语替代，直至五年级的教学也无须出现单位“1”的概念，让最初的词语表达规范，也避免延迟的抽象与替代，不增加学生的认知负担；二是舍弃了“平均分”这一词语，用学生容易理解的“几个相等的部分”直接替代，既突出部分和相等，也易于学生理解。数学语句要契合儿童的语言习惯，教学要在自然的活动中展开，然后再进行分析、概括、结构化，有助于概念学习过程中的顺畅交流、构建联系。

四、联通整数与分数，感悟数学的创生

从10以内的数到多位数，从整数的计数单位到十进制原理，以及对数的感觉，学生已经积累了丰富的认数经验。由于分数具有数的属性，这些经验会成为学生认识分数的基础；由于分数与整数计数单位不同，这些经验也会对认识分数产生困扰。教师要尝试勾连它们的联系，突出分数的独特价值与魅力。

【活动四】

教师让学生自由折纸，折叠出一个几分之一。把表示相同分数的图形在同一区域展示。

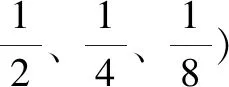
[总结]分数和整数一样，都能在数直线上找到位置。

皮亚杰的研究指出，当儿童操作再细分的部分或子分割时，他们了解到此细分的部分是全体的一部分，同时这个细分的部分本身也是一个可以再细分的全体。整数与分数的区别就在于计数单位的不同，学生理解了分数的计数单位，才能顺利地将分数纳入已有知识结构。一是体现了分数与整数都是有大小的，但几分之一的分母越大，分数却越小，与整数的大小顺序是相反的；二是体现了分数都可以在数轴上找到位置，分数与整数在数的大家庭中共存；三是突出分数与整数都具有可加性，不同的是分数需要用部分去细分整体，先分再数，分好了，下面的步骤和整数也就统一了。最后观察图形，引导学生感悟视角的不同，能看到整数，也能看到分数。

面对学生，教师不仅需要思考教学内容的本质是什么，还需思考如何循着他们的现实基础、兴趣感悟数学知识的本质以及其中蕴含的智慧。作为教师，应尊重学生的已有经验，遵循学生心理发展特点，再结合自己的教学实践经验寻求接近数学本质的路径，并敢于在课堂中行动、尝试，从一点点的改变中努力激发学生对数学的兴趣，掌握数学中的符号与规则。