一个关于投资组合损失风险价值界的注记

（广西师范大学 广西 桂林 541006）

一、绪论

对于随机损失变量X=(XI,..., Xd) 表，其在置信水平α э )0,1(э处的风险价（（简记为Va））被定义为

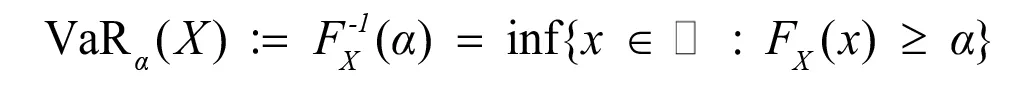
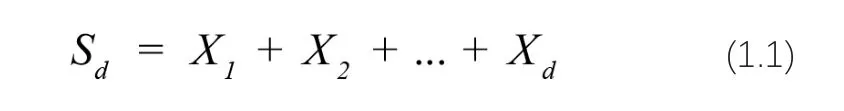
对随机损失向量X的风险范围进行估计，主要就是给出VaRa(Sd)的上、下界。为此，我们可以定义

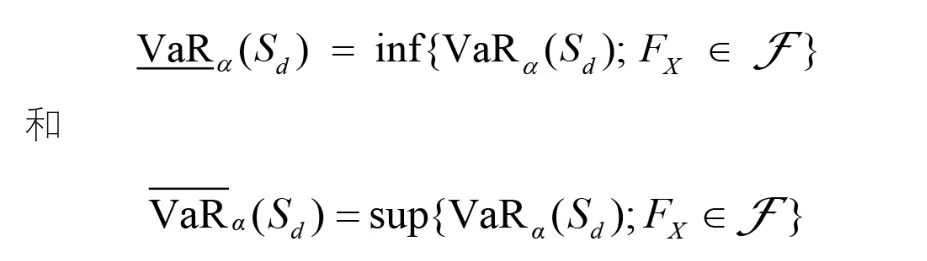
其中F是由对应于边缘分布(FI,..., Fd) 的所有可能联合分布集。显然，对于任意具有联合分布我们都可以得到

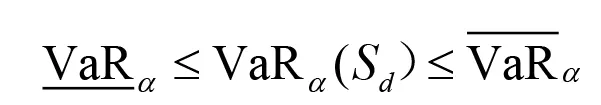
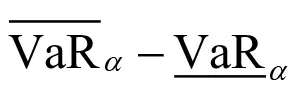
如果单个风险之间差异比较大，那么等加权情形就可能会导致风险分散的效果非常有限。例如，一个风险Xi遵循参数为λ的泊松分布，另一个遵循参数为θ＞0 的Pareto分布。故而应该考虑权重不相等的情形。这就促使我们研究一般加权风险组合下VaR的界，即找出的上、下界，其中

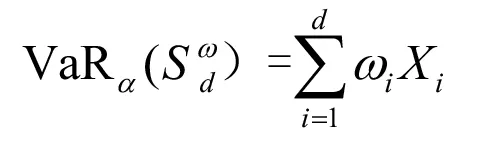
对应的加权损失向量为

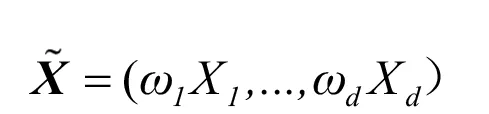
二、加权风险向量独立条件下的VaR界

特别地，如果E(Y) 表示Y的有限均值，那么

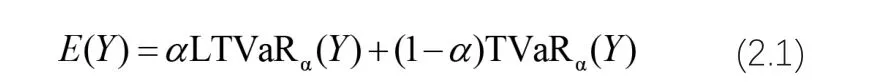
此外，我们定义了两个随机变量X和Y之间的凸序为：X≤cxY，对于任意的α э )0,1(，X≤cxY 成立当且仅当TVaRa(X) ≤ TVaRa(Y) 以及 X≤cxY 意味着X和Y具有相同的均值，因此对于任意的α э )0,1( ，X≤cxY成立当且仅当

是k个服从(0,1)上均匀分布的独立随机变量并定义。

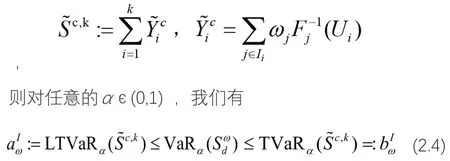
三、风险向量部分独立条件的VaR界

采用与定理2.1类似的证明方法可得如下定理。

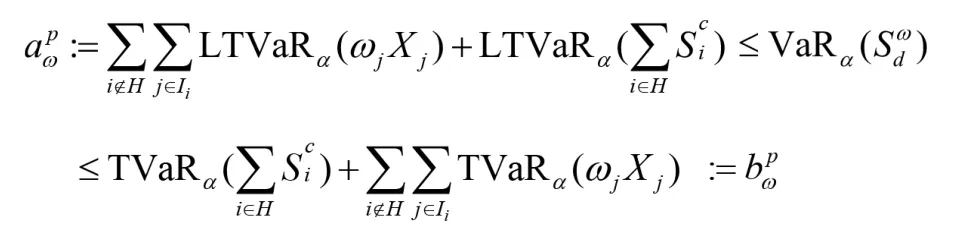
对于任意我们可以得到

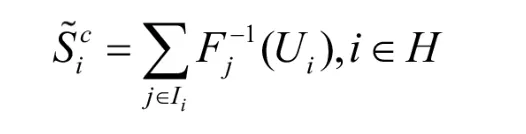
结束语：

本文通过引入独立和部分独立的条件，将加权风险向量分成若干个独立的子向量，对不同风险向量赋予不同权重最终得出了投资组合损失风险价值的上、下界，且所得界比无约束条件下投资组合界更优。