基于动态聚类的卫星导航信号多波束抗干扰方法

郑雅萍，赵璐璐，龚文斌，邵丰伟，常家超

(1.中国科学院微小卫星创新研究院，上海 200120；2.中国科学院大学，北京 100049)

0 引言

卫星导航系统是人类导航史上的重要突破.它能连续提供高精度和高速度的导航、定位和授时信息.然而由于导航信号到达地面时非常微弱，极易受到外界射频信号的干扰，因此研究导航信号的抗干扰方法具有重要意义.自适应波束形成[1]是一种利用阵列天线方向图特性实施的空域抗干扰技术，既能在干扰方向形成零陷，又能对卫星信号进行增强，使整体输出具有最大的信干噪比(SINR)，可提高导航接收机的抗干扰性能[2-4].

导航通常需要同时接收多颗卫星信号，多波束抗干扰技术能针对不同卫星信号形成多个波束.在波束指向上，传统方案一般采用固定波束指向.文献[5]提出一种固定一个波束指向法线方向，其余波束均匀分布的指向方法；文献[6]将信号空间分为多个子空间，通过最优分配策略选取多个子空间分别实现固定波束指向；文献[7]对多波束固定指向的方位角和俯仰角的数目进行了分析；文献[8]在改进STAP[9]算法的基础上，对多波束的指向角的角度做了分析.由于通常情况下导航接收机可以同时接收的导航卫星信号较多，为了减轻导航接收机的处理压力和降低硬件资源开销，通常难以做到波束数大于等于接收信号数.因此在多数情况下，接收信号数要多于波束数，此时传统固定指向角的方法一般无法兼顾所有卫星信号[5-8].

针对传统方法的缺陷，本文提出一种基于最小方差无失真响应(MVDR)[10]的动态指向多波束抗干扰方法.该方案通过获取卫星信号来向的先验信息，利用K-means 聚类算法，提取信号来向的聚类中心，以该中心为波束形成的约束方向，保证每颗卫星拥有较高输出的SINR，提高整体的抗干扰性能.

1 多波束抗干扰技术

1.1 自适应波束形成

自适应波束形成技术是一种有效的干扰抑制技术，它克服了时域、频域信号处理的局限性，在空域对干扰进行处理.其原理图如图1 所示.

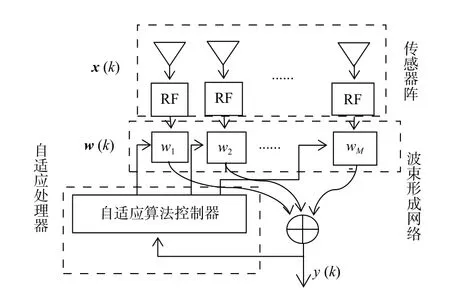
图1 自适应波束形成技术原理图[11]

假设阵元数为M，则k时刻一组接收信号为

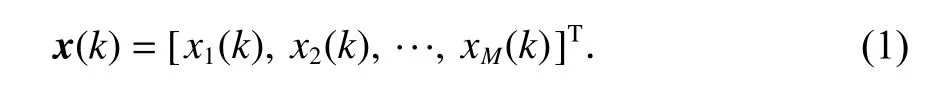
若自适应处理器输出的加权矢量为

则对应的输出信号可以表示为

在波束形成算法中，MVDR 通过约束权矢量，可以使输出信号拥有最大SINR，且无需期望信号序列的先验信息.MVDR 目标函数可表示为：

式中：RXX=E{x(k)xH(k)}为阵列接收信号的自相关矩阵；a(θ,φ)为波束导向矢量，θ 和φ分别表示目标波束指向的俯仰角和方位角.M个阵元组成的平面阵的导向矢量a(θ,φ)可以表示为[12]

式中：k=−ω/c[sinφcosθ,sinφsinθ,cosφ]T是对应于方向(θ,φ)的波数向量；ω 为信号圆频率；c为光速；pm=[pxm,pym,pzm]T是第m个阵元的位置坐标向量.

根据式(4)建立拉格朗日函数，可求得最优权值如下：

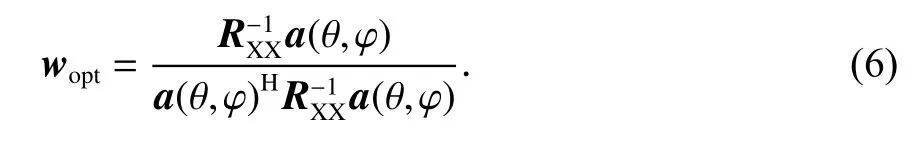
图2 为七元均匀线阵MVDR 的波束方向图，由图2 所示波束，方向在干扰方向(20°和60°)处均形成了较深的零陷，起到抑制干扰的作用，同时波束主瓣对准信号方向(40°)，对有用信号产生增益，从而实现空域滤波的目的.

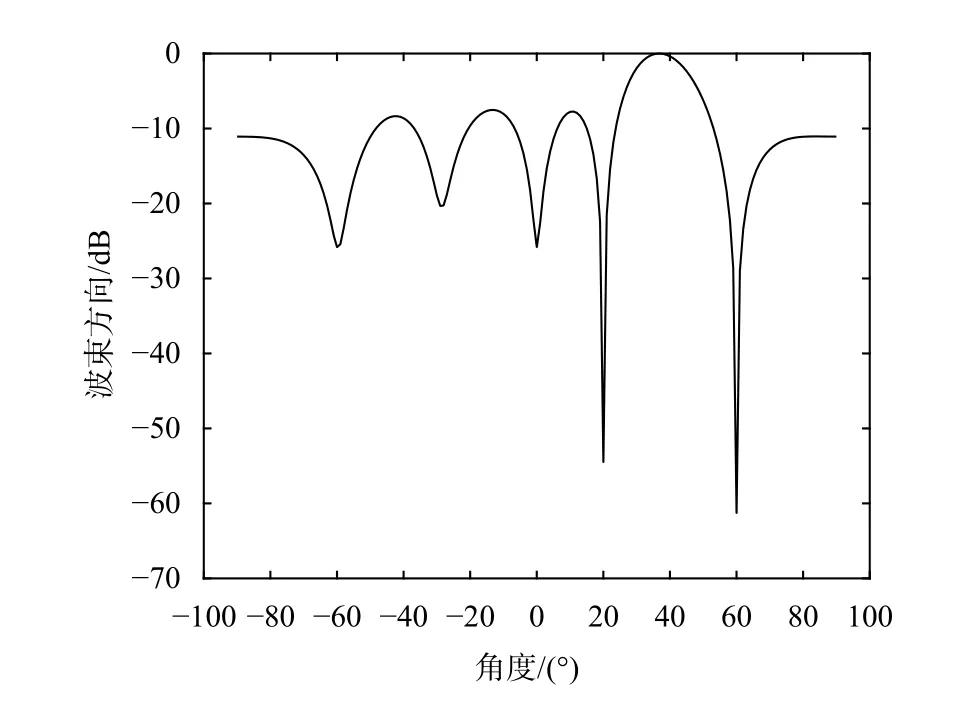
图2 MVDR 波束方向图

1.2 多波束技术

由1.1 节可知，自适应波束形成技术能较好地实现信号的抗干扰.但在实际导航中，往往需要同时接收多颗卫星信号，多波束技术可以针对不同卫星自适应地形成多个波束.

多波束抗干扰的原理框图如图3 所示，当波束数目为N，卫星数目为NS，干扰数目为NJ时，第ns个信号的来向为(θns,φns)，第nJ个干扰的来向为(θnJ,φnJ)，则k时刻接收信号可表示为

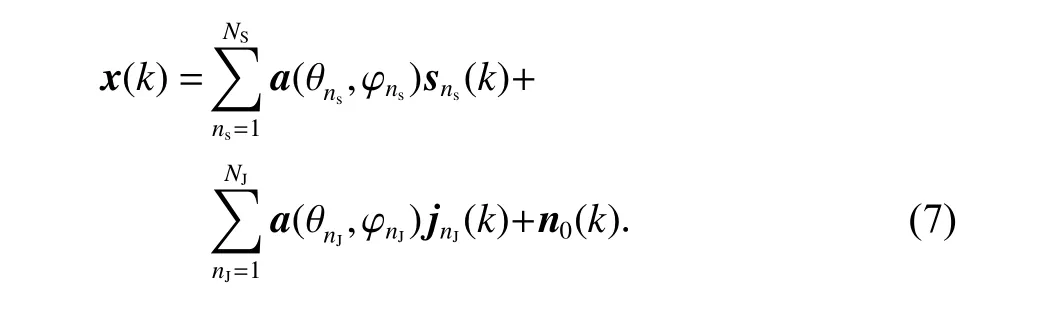
式中，sns(k)、jns(k)、n0(k)分别表示k时刻第ns个卫星信号，第nJ个干扰以及阵列天线的噪声矢量.

图3 多波束抗干扰原理框图

第n个波束的目标函数可以表示为：

化简后，可得

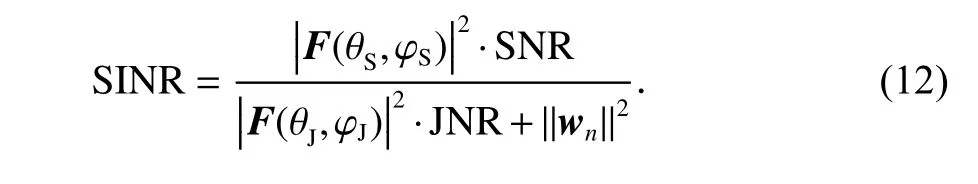
式中：SNR 等于PS/Pn，表示输入SNR；JNR 等于PJ/Pn，表示输入JNR.

2 波束指向方向

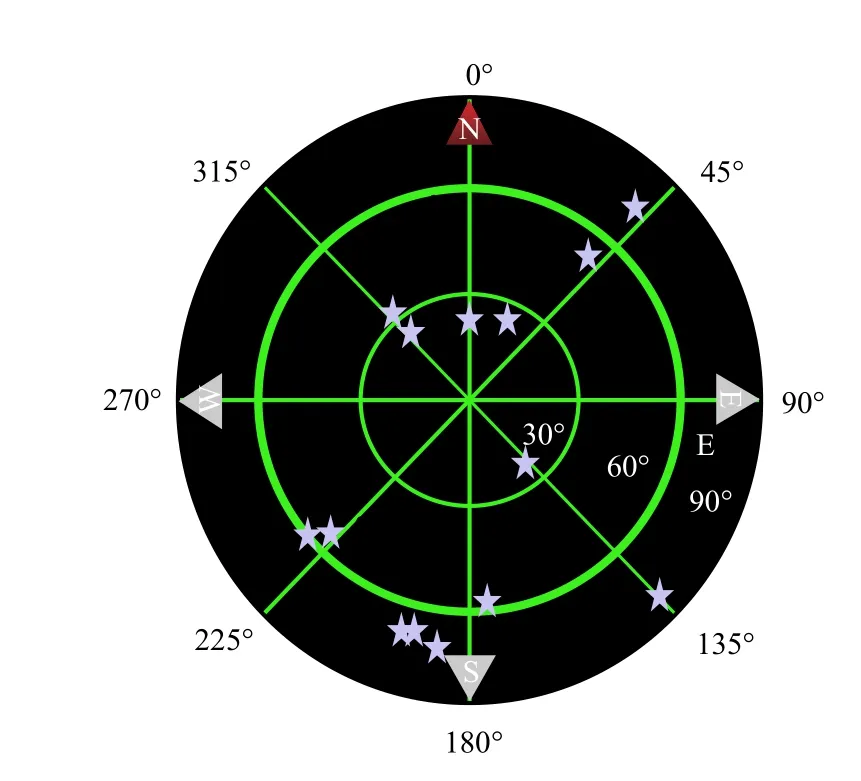
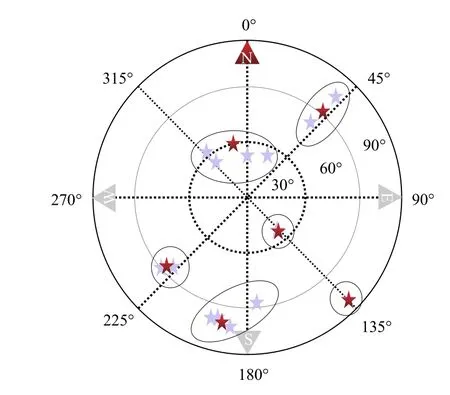
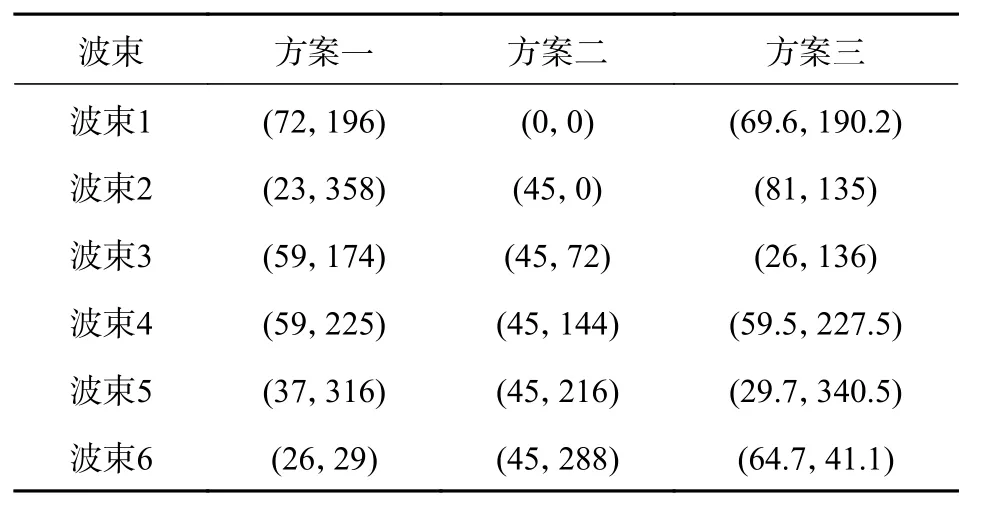
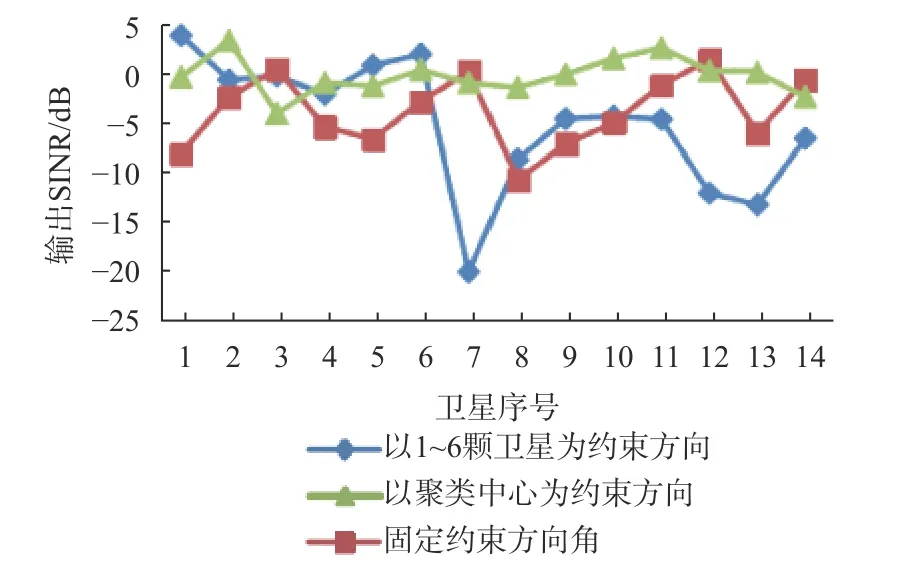
在多波束抗干扰技术中，波束指向(θn,φn)的选择决定了波束主瓣的方向.当条件受限，无法形成与卫星数相等的波束，即N

根据卫星星历数据，可以估计卫星信号大致来向，据此提出一种新的动态波束约束方式.该方法根据卫星信号来向的先验信息，利用K-means 聚类算法，将卫星信号来向分成N类，提取信号来向(θ,φ)的聚类中心，以该中心为波束形成算法的约束方向.

具体步骤如下：1)设定波束数目为N，读取卫星信号来向数据(θ,φ)；2)初始化聚类中心，在数据长度范围内随机产生N个不同的值，以此为下标提取对应的卫星信号方向，作为聚类中心；3)分配信号来向数据点，将信号来向数据分配到与各初始聚类中心欧氏距离最近的聚类，产生列表，并计算平均误差；4)以每一类所有点的平均值作为新的聚类中心，更新聚类中心，再次将数据分配到与各个新的聚类中心欧氏距离最短的聚类，产生新的列表，计算误差；5)比较前后两次误差，若不相等则继续重复步骤4)，否则终止循环.流程图如图4 所示.

通过该算法产生N个聚类中心，以此作为N个波束的约束方向(θn,φn)，代入多波束的数学模型，即式(8)，最终实现多波束抗干扰.

图4 聚类算法流程图

3 仿真实验及结果分析

建立一个八元均匀圆阵，半径R等于半波长.图5 为均匀圆阵的布阵模型，以参考地为原点，正北为x轴，正东为y轴，垂直xoy平面的法线为z轴，建立坐标系.

假设波束数目为6，干扰来向(40°，90°)，输入JNR 为40dB；卫星信号参考：时间2020-12-30T20：08：00，地点31°12′N，121°36′E 处可见的14 颗北斗卫星信号，输入SNR 为−20dB.卫星实时分布图如图6 所示，信号来向(θ,φ)如表1 所示.

基于该天线传感器阵模型，对以下三种约束方案进行仿真分析：

方案一，随机选取6 颗卫星信号来向作为波束指向，本文以1～6 颗卫星为例；方案二，据文献[4]所述，固定一个波束于法线方向，其余五个波束的俯仰角θ 固定为45°，方位角φ在空间范围内均匀分布；方案三，对卫星信号来向数据采用K-means 聚类算法分析，获取6 个信号来向的聚类中心作为波束指向.聚类分析结果如图7 所示，其中红星代表各个聚类中心.以上三种方案的波束指向角如表2 所示.

图6 卫星实时分布图

表1 卫星信号来向(°)

图7 卫星分类及聚类中心示意图

表2 波束约束角度(°)

图8 为方案三的其中一个波束的方向图，约束方向为第一个聚类中心(69.6°，190.2°).由图可知，方向图在干扰方向(40°，90°)处产生了较深的零陷，在约束方向处拥有最高增益，从而使附近的卫星信号也拥有高增益.

图8 圆阵方向图

图9 为三种方案的输出SINR 对比图.由图可知，方案一除了1～6 颗卫星，其余卫星的输出SINR较差，且参差不齐.方案二即固定约束方向角，相较方案一总体性能有所提升，但仍有部分卫星信号的输出SINR 较低.可见当卫星信号数目大于波束数目时，传统的约束方向并不能实现对全部卫星信号的高质量接收.而本文采用K-means 聚类算法将聚类中心作为约束方向，能够有效地兼顾每一颗卫星的信号，使14 颗卫星信号均拥有高增益，从而使整体的输出SINR 保持在一个较高的水平.

图9 信号输出SINR 对比图

4 结束语

针对导航信号抗干扰的问题，提出了一种基于K-means 聚类算法的动态指向多波束抗干扰方案.该方案将卫星信号来向数据(θ,φ)通过K-means 聚类算法进行聚类分析，获取聚类中心作为多波束的指向.以实际接收到的14 颗北斗卫星信号的方位信息为参考，建立天线阵模型进行仿真，结果表明当卫星信号数目大于波束数目时，本文提出的方案较传统固定波束的方法有更优的性能，能有效地保障每颗卫星的输出SINR，提高了整体的抗干扰性能.