INS/GNSS/ODO 嵌入式系统的容错技术研究
(武汉大学卫星导航定位技术研究中心,武汉 430079)
0 引言
在嵌入式组合导航系统中,传感器短时间的故障对系统稳定性有很大影响.自适应卡尔曼滤波可在全球卫星导航系统(GNSS)定位精度突变的情况下保证定位的精度[1].而该算法是在假定只有GNSS 粗差的情况下使用的.GNSS/惯性导航系统(INS)组合导航中,传统的χ2检验可以判断出系统是否存在故障,不过其不能区分出故障所在的传感器[2].基于神经网络的χ2检验方法和利用粒子滤波的故障检测方法可辨别出故障传感器[3-4].由于其计算开销较大,并不适用于嵌入式导航系统.
在所有故障中,GNSS 故障对组合导航的性能影响最为显著,且该故障可分为软故障和硬故障[5-6].当GNSS 整体的可观测性较差时,检测灵敏度较低的残差卡方检验将在GNSS 软故障下偏离真实值[7].任旭阳[8]提出基于贯序概率比检验法(SPRT)的故障检测算法对软故障的检出具有较好的效果,但该算法并不能对故障进行及时地隔离及纠正处理.张浩等[9]提出的双状态卡方故障检测系统对具有高精度惯性测量单元(IMU)系统的GNSS 软故障具有较好的效果,该方法并不适用于低成本IMU 组合导航系统,并且双状态同时面临着INS、里程计(ODO)等故障污染的风险.
隧道、林荫道等复杂环境下,实时动态(RTK)定位结果无法长时间保持在固定解,因此本文针对这一问题实现了基于多GNSS 状态的INS/GNSS/ODO抗差组合导航算法,提高了系统对GNSS 状态的容错性.同时,在此基础上提出了一种两级故障检测方法,提高了系统对各传感器故障的容错性.其中,第一级检测使用了基于解析冗余[10]的残差卡方检验法,可检验出ODO、INS 和部分GNSS 故障,并保证了第二级检验的状态传播过程不受污染.第二级检测使用了改进的双状态传播卡方检验算法,可用于进一步检出GNSS 软故障.
1 INS/GNSS/ODO 组合导航
1.1 状态方程
INS/GNSS/ODO 松组合导航系统选取十六维向量作为系统状态向量,

式中:δr为位置误差;δv为速度误差;ψ为姿态误差;bg为陀螺仪零偏;ba为加速度计零偏;δk为里程计标度因子误差.
系统状态方程可表示为
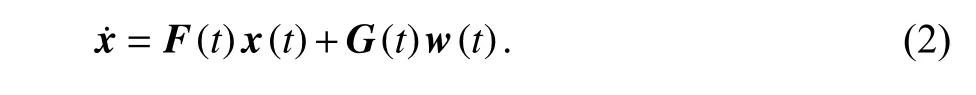
式中:F(t)为状态转移矩阵;G(t)为系统噪声驱动矩阵;w(t)为系统噪声.该系统是以GNSS、ODO 辅助INS 的形式运行的.
在式(2)中,状态转移矩阵推导自INS 的误差方程,常用的有ψ 角误差模型[11]:

式中:f为加速度计输出的比力;δg为重力误差;投影坐标系b系为载体坐标系;投影坐标系c系为计算坐标系;p系为平台坐标系;ψ 为c系到p系间的误差角.
根据机械编排误差模型和MEMS 的一阶马尔可夫模型可得到离散的状态转移矩阵,如式(6)~(8)所示[18]:

式中:RM为子午圈曲率半径;RN为酉卯圈曲率半径;g为当地重力;h为地理高度;∆t为时间更新的时间间隔;ϕk/k−1为离散形式的状态转移矩阵;i系为地心赤道惯性系;e系为地心地固系;n系为导航系.

1.2 量测方程


1.3 基于多GNSS 状态的抗差滤波
当林荫道、隧道等复杂场景下,GNSS 信号容易受到影响,RTK 解在固定解、浮点解、抗差解和无有效解四种状态下变化.GNSS 量测不确定协方差矩阵

式中:Ξ()函数将向量变换为对角矩阵,同时非对角线上元素全为0 的方阵;σ2为具体GNSS 状态下的通过参数估计法获取的三轴上协方差向量.
由于R1的不连续性,在R1从低定位精度解状态变为低定位精度解状态时,系统状态量可靠性不高,系统检出量测粗差或故障的能力差.同时GNSS 量测中存在较多的粗差,故可根据式(23)~(32)所表示的抗差滤波算法对组合时的量测不确定性进行调整[13].

式中:Qk为系统状态动态变化中噪声的协方差矩阵;Ση为任意参量η的协方差矩阵;为预测残差,又称为新息[14];为量测不确定协防差矩阵R1,k的参数估计值;N 表示参数估计的窗口大小;βk为抗差因子;在贯序卡尔曼滤波中,下标1 特指GNSS的量测更新过程.
由于模型中错误地判断GNSS 固定解将对系统的稳定性造成的影响极大,在滤波前可使用GNSS 位置精度因子(PDOP)对可疑值进行剔除.

式中:pdop为测得的PDOP 值;CBAD为给定的阈值常量.
抗差滤波算法可以降低GNSS 粗差的影响,但是在假定其仅有GNSS 异常下进行的,当ODO 异常或机械编排结果异常时,抗差滤波反而会降低组合结果的精度.同时当GNSS 在一段时间内出现偏差时,抗差的效果并不如故障检出后将GNSS 屏蔽的效果好.
2 故障检测系统
2.1 传统的预测残差卡方故障检验法
χ2故障检测是一种通过判断n维高斯分布的随机向量的均值是否与假设一致来判断系统是否故障的方法.根据随机向量选取的不同,可分为基于状态向量的χ2故障检测和基于残差的χ2
根据式(25)和式(29),可构造评价函数


2.2 改进的双状态传播卡方故障检验法
如图1 所示,双状态传播χ2故障检测器由双状态传播器和卡方检验器组成.其中双状态传播器又由两个相互独立的状态传播器及其控制开关组成,状态传播过程是从标准卡尔曼滤波中独立出来的.

图1 双状态传播卡方故障检测器
传统的双状态传播χ2故障检测法一般用于具有高性能IMU 的系统中.由于消费级MEMS 的精度较差,状态传播的误差呈指数增长,导致故障检出率比传统的残差χ2故障检测法差.针对这一问题,如图2所示,本文在状态传播器后增加了ODO 量测更新单元,使状态递推的误差在一定时间内呈线性增长趋势.
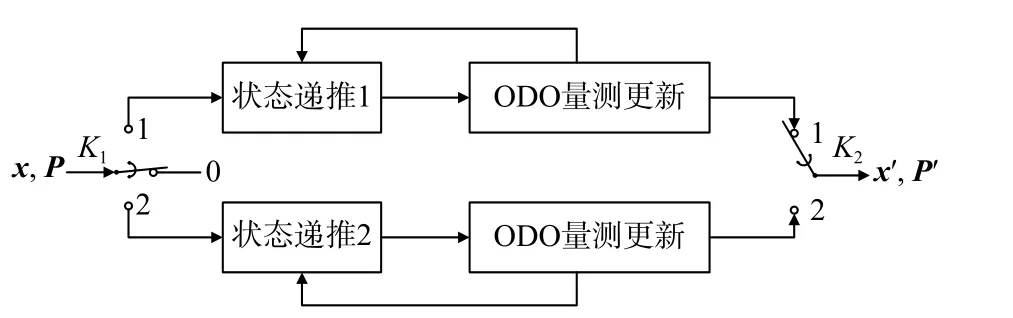
图2 改进的双状态传播器
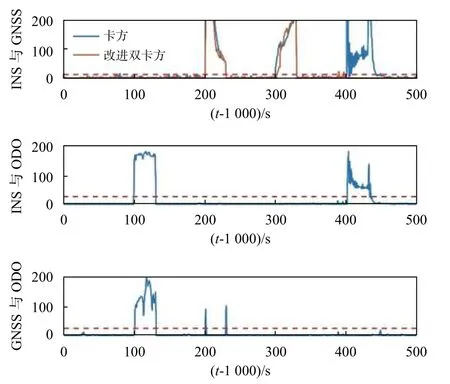
为了理论验证改进算法的有效性及适用范围,以单轴线性软故障为例,当故障发生时GNSS 立即屏蔽.并假设线性软故障增长率为a,各轴的状态递推误差增长率均为b(b 可化简为 上述的两种方法可以用于检测系统是否故障,但严格意义上并不能锁定故障的出现位置.另一方面,双状态传播卡方故障检测法虽然能够处理GNSS 软故障,但其同时面临着ODO 故障或INS 故障污染的风险.相较于不使用该方法,当ODO 故障或INS 故障发生时,系统将变得更不稳定[17]. 针对上诉两个问题,本文提出了一种两级故障检测系统,如图3 所示.在第一级检测中,系统分别计算出三组新息及卡方值,并在故障检测判决器中通过基于解析冗余的故障检测方法来初步锁定故障位置.当系统认为第一级检测并不足以检测出GNSS 软故障时,系统将通过改进的双状态传播卡方故障检测法进行进一步判断. 图3 基于解析冗余的故障检测系统模型 由式(37)可知,GNSS 量测的精度远大于INS/ODO 航迹推算的位置精度,第二级检测将被跳过,故可根据RTK 定位是否为固定解设计如表1和表2 所示. 在故障处理方面,当GNSS 故障出现时,系统屏蔽GNSS 量测更新.当ODO 出现故障时,系统屏蔽包含改进的双状态传播χ2故障检测器在内的ODO 量测更新,同时不对ODO 标度因子进行反馈和修改.当INS 发生故障时,系统将对改进的双状态传播χ2器重置及屏蔽处理,防止状态传播器内的状态受到污染,同时适当调节Q 阵的自适应组合导航算法避免组合导航系统发散. 表1 RTK 固定解时的第一级故障判决表 表2 含噪定位解时的第一级故障判决表 图4 为GN310 嵌入式系统,车载实验的核心装置为自主研制的一款具有通信导航一体化功能的低成本嵌入式系统—GN310.该系统通过4G通信从千寻获取RTK 差分改正数并在内部GNSS芯片中进行单频RTK 计算,在开阔环境下可获取厘米级定位精度信息. 图4 GN310 嵌入式系统 为了提高在复杂场景下的鲁棒性,系统内还集成了IMU、磁力计等器件,其中IMU 的性能如表3 所示.系统通过DB9 接口接入分辨率为2000P/R 的编码式里程计即可运行GNSS/INS/ODO组合导航算法,并实时输出高精度强鲁棒性位置速度等信息.实验使用的参考系统为装有光纤陀螺、双频RTK 的GNSS/INS 紧组合系统NovAtel CPT6.实验过程中使用表4 中参数对组合导航原始观测数据进行修正. 表3 IMU 性能指标 表4 修正参数 实验时长为1 000s,INS 运算频率100Hz,ODO 量测更新频率10Hz,GNSS 量测更新频率均为1Hz,平均车速为40km/h. 如图5 所示全路段经过四次隧道,路段中存在多处林荫道,路段中存在的3 处实为浮点解或抗差解被错误判为固定解的GNSS 结果.水平位置误差如图6所示,x轴中,黄色点表示浮点解,占总测试时长的40.6%;粉色表示抗差解,占总测试时长的3.1%.标准卡尔曼滤波下,水平位置均方根误差(RMSE)为0.67m;多GNSS 状态抗差滤波下,水平位置RMSE为0.42m,定位效果提升39.7%. 图5 实验路段 图6 水平位置误差与时间的关系 考虑到实测中同时可遇到多种故障的情形有限,本节选用另一组全路段固定解的数据进行半实物仿真[15].测试路段平均车速为30km/h.分阶段施加ODO 故障、GNSS 硬故障、GNSS 软故障和INS故障.如表5 所示,仿真过程分为两组,第一组在RTK 固定解下进行,第二组在含噪声定位解下进行.其中含噪声定位解在RTK 固定解的基础上各轴添加1m 高斯白噪声来模拟. 表5 故障条件 在RTK 固定解的情况下,故障检测值如图7所示,故障屏蔽效果如图8 所示,其中硬故障值与真值的差在故障区间内为常向量,而软故障值与真值的差在故障区间内为递增向量.根据表5 的判决条件,表中的四种故障皆能有效地辨别出.在GNSS 渐变故障时,改进双状态传播卡方检测算法与残差卡方检测结果接近,故嵌入式系统中可跳过双状态传播卡方检测算法的计算,实现降低计算量的目标. 图7 RTK 固定解下的卡方故障检测 图8 RTK 固定解下故障屏蔽效果 在单点定位解时,标准和改进的双状态传播器的窗口长度都为10s.如图9 所示,第一层故障检测能检出ODO 故障.图10 是根据先验已知的故障时间来屏蔽GNSS 量测更新,由于低成本嵌入式组合导航系统的IMU 性能较差,故标准的双状态传播卡方检测效果较差. 图9 含噪声定位解下的卡方故障检测 图10 含噪声定位解下根据时间屏蔽的卡方结果 在根据实际的检测阈值处理故障时,如图11所示,在GNSS 软故障发生时,由于故障初期残差卡方检测法未能检测出该故障,组合导航结果被拉偏.而改进的双卡方检测法在故障发生后的第15s 时检测出并修复了故障,从而保证了系统的稳定性和可靠性. 图11 含噪声定位解下的卡方故障检测 本文提出了基于INS/GNSS/ODO 抗差组合导航算法的两极故障检测方法,第一级检测使用了基于解析冗余的残差卡方检测法,第二级检测使用了改进的双状态传播卡方检测算法.相比于传统故障检测方法,该容错方法能够有效地处理ODO、INS 故障和GNSS 软故障,提高了系统的导航性能和鲁棒性.该算法除了能够用于检测硬件故障,同时还能够在车辆轮胎空转和侧滑、ODO 接口接触检测、GNSS 防欺骗等方面起到积极作用,具有良好的工程应用意义. 致谢:西北工业大学自动化学院严恭敏老师和武汉大学卫星导航定位技术研究中心牛小骥团队的讨论.
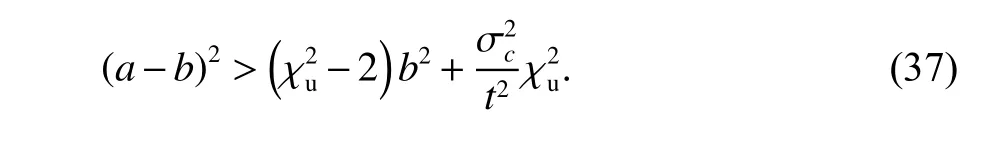
2.3 两级故障检测系统模型



3 实验仿真与实验分析
3.1 路测装置及实验条件



3.2 抗差组合导航的仿实时实验


3.3 故障检验系统的半实物仿真





4 结束语

