基于5G 毫米波到达时间差的室内定位算法

李芳馨，涂锐,3，韩军强,3，张垠，洪菊

(1.中国科学院国家授时中心，西安 710600；2.中国科学院大学，北京 100049；3.中国科学院精密导航定位与定时技术重点实验室，西安 710600)

0 引言

如今，全球卫星导航系统(GNSS)及其区域增强系统可以为户外用户提供高精度的导航定位服务.然而，卫星信号难以穿透墙壁，导致其定位性能在室内会受到严重影响[1].但大型商场、综合医院、机场等建筑、地下停车场、地下轨道等交通设施日新月异，此类场景下的定位需求在日益迫切的情况下，室内定位成为当前定位技术领域的重点研究方向之一.

随着第五代移动通信技术(5G)的兴起，5G 定位技术得到了越来越多的关注.5G 毫米波信号的带宽大，所以其可以提供克拉美罗界更小的参数估计误差[2-3]；毫米波频率高，所以多路径效应造成的频率选择性衰落更明显，因而多径干扰少；5G 采用大规模天线阵列(Massive MIMO)与波束赋形技术，因此具有更高的测距和测角精度[4]；5G 采用了低时延、高精度同步等技术，也有利于基于时间测量值精度的提升.同时，与其他室内定位方法，如Wi-Fi、蓝牙、行人航位推算(PDR)、超宽带(UWB)等[5]相比，基于5G 的室内定位技术还有以下优势：1)基站布设范围广；2)具有统一标准；3)不需要额外的定位设备和终端.因此，5G 的发展为室内高精度定位提供了新的技术途径.

虽然5G 定位还是一个相对比较新的词汇，但蜂窝无线定位的研究已经有多年的历史.Caffery 等[6]在其论文中全面阐述了蜂窝网络无线定位的概念和基本技术，在总结和概括众多研究者研究成果的基础上，深入研究了降低多路径效应影响的高精度到达时间(TOA)无线定位算法.Foy[7]利用泰勒级数展开算法将基于到达时间差(TDOA)的观测方程线性化，然后迭代解算未知点坐标.Chan 等[8]提出了利用两次加权最小二乘法(WLS)方法计算未知点坐标，在多路径效应不明显的情况下计算速度快，并且定位效果优异.Chen[9]提出使用残差加权的方法来消除多路径效应带来的误差.熊瑾煜等[10]深入研究了Taylor 级数展开算法，并提出使用WLS 法估计未知点的初始坐标，再通过Taylor 级数展开算法确定最终结果，获得了更快的收敛速度.白杨[11]将数据挖掘和机器学习技术应用于定位中，通过分析大量测量数据，得出了具有鲁棒性的定位结果.近两年也有一些学者对5G 定位展开了研究.张书楠[12]研究了基于TOA 的5G 毫米波定位算法.付加伟等[13]通过5G 接收天线阵元间的相位差测量信号到达角，利用码片相位差测距，最后综合测角和测距得到定位结果.但总体来说，目前关于5G 定位的研究还比较少，5G 定位的研究具有重大应用价值.

本文研究了室内的5G 毫米波定位算法，基于TDOA 定位原理，对比分析了三种算法在静态和动态环境中的定位效果，得到有应用价值的结论.

1 定位方法

因为TOA 定位和TDOA 定位实现简单，解算精度高，所以是蜂窝网络定位中最常用的技术.TOA 算法通过测量接收机与基站之间的绝对时间差，得到绝对距离，然后联立方程组解算圆球交点，求得未知点坐标，因此TOA 算法要求接收机时钟和各个测量基站时钟严格同步.而TDOA算法的测量值可以通过TOA 测量值求差来获得，所以TDOA 算法对接收机时钟与基站时钟是否同步不做要求，同时特征差值还可以消除部分系统误差.因此，与TOA 算法相比，TDOA 算法定位精度更高，对环境的适应性也更强.下面将介绍本文实验中使用的基于TDOA 的CHAN算法、Taylor 级数展开算法以及提出的一种顾及接收机与基站时间差的LLOP 算法.

1.1 基于TDOA 的CHAN 算法

设Ψ′为Φ′的协方差矩阵，

最终，未知点位置估计为

式中，正负号可以通过第一次最小二乘得到的初始坐标(x,y,z)来判断，选取与初始坐标相近的值，消除解的模糊性.

1.2 基于TDOA 的Taylor 级数展开算法

根据CHAN 算法第一次加权最小二乘得到的坐标(x,y,z)，对式(3)进行二阶Taylor 级数展开，得到

利用加权最小二乘方法，可以得到∆的估计为

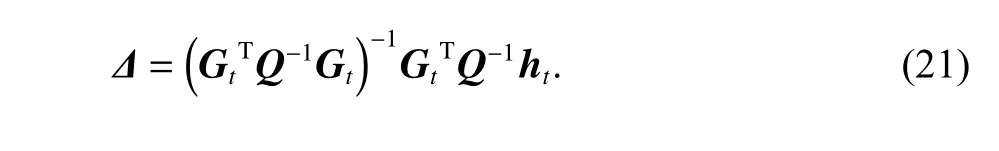
Taylor 级数展开算法得到的未知点位置估计为

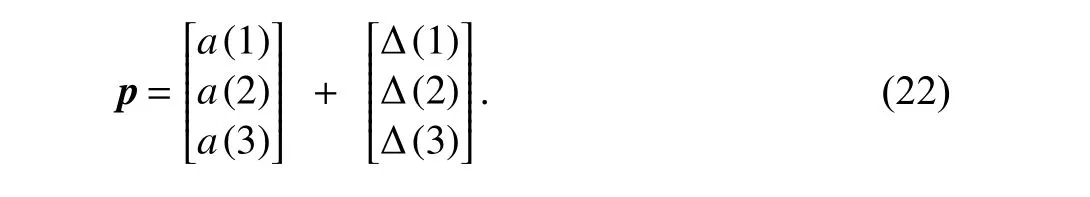
1.3 顾及接收机与基站时间差的LLOP 算法

设接收机与基站之间的时间差为T.则接收机到第i个基站的距离

代入式(1)，并减去Ri，可得

式中：ΦLLOP为误差；

2 实验及分析

2.1 实验平台

在中国科学院国家授时中心西安场区办公楼地下室布设了5 个5G 微基站，如图1 所示，蓝色五角星图标为基站位置，黑色“+”字为静态定位的参考点位坐标.

图1 5G 室内定位实验环境图

实验中采用了局域坐标系，5 个基站的X、Y、Z坐标分别为：基站A(13.731，27.501，3.205)m；基站B(0.192，28.078，3.322)m；基站C(0.461，11.937，3.499)m；基站D(0.501，1.161，3.483)m；基站E(14.645，1.326，3.492)m，因为各个基站的Z坐标相差很小，如果利用三维方式直接解算将会造成很大的误差，因此使用了约束平差的方法，根据实验环境的实际情况，将Z轴约束为固定值后，再进行解算.

2.2 实验结果与分析

2.2.1 5G 室内静态定位

本文使用5G 观测值进行定位，比较了三种基于TDOA 的算法.如图2 所示，图2(b)黑色“+”字为参考点位，红色“*”字为分别使用CHAN 算法、图2(c)为Taylor 级数展开算法、图2(d)为顾及接收机与基站时间差的LLOP 算法得到的估计点位.

图2 静态定位结果

第一种方法是经典的CHAN 算法，结果如图2(b)所示.首先将TOA 观测值作差，消掉基站与接收机之间的钟差，然后联立观测方程，并将其伪线性化处理，得到以未知点坐标(x,y,z)和未知点到基准基站的距离R1为未知数的方程组，利用残差加权的最小二乘法解算得到初始坐标，然后利用初始解将非线性方程线性化，再通过一次最小二乘方法得到最终结果.静态定位结果的均方根误差(RMSE)为0.2856m.

第二种方法为Taylor 级数展开算法，结果如图2(c)所示.Taylor 级数展开算法因为具有精度高和适应性强等特点，在求解非线性定位方程组中得到了广泛的应用，但如果给出的初始值准确性差，则会严重影响该算法的性能，因此初始值必须符合一定的精度要求，另外，接收机与基站的位置关系也会影响算法的收敛.本文使用CHAN 算法将第一次最小二乘后得到的结果作为未知点坐标的初始值，然后使用Taylor 级数展开算法进行迭代运算，确定用户坐标.它的RMSE 为0.3387m.

另外，本文提出了一种顾及接收机与基站时间差的LLOP 算法.经典的LLOP 算法是基于TOA 的，因此要求接收机与基站时间同步，所以在传统LLOP 解算中增加了接收机与基站时间差这一参数，同时使用残差定权.这个方法的RMSE为0.3653m.它的计算复杂度小于经典的CHAN算法和Taylor 级数展开算法，因此有更快的解算速度，同时定位精度与两者相差不大，可以满足室内一般的定位需求.

2.2.2 5G 室内动态定位

图3 展示了基于5G 测量值的CHAN 算法、Taylor级数展开算法和顾及接收机与基站时间差的LLOP算法的室内动态定位结果如图3 所示.图3(b)黑色“+”字为参考点位，红色“*”字为分别使用CHAN 算法、图3(c)为Taylor 级数展开算法、图3(d)顾及接收机与基站时间差的LLOP 算法得到的估计点位，而蓝色连线则是经过卡尔曼滤波后得到的估计轨迹.

图3 动态定位结果

在滤波前，CHAN 算法的RMSE 为2.9877m，Taylor 级数展开算法的RMSE 为2.2580m，顾及接收机与基站时间差的LLOP 算法的RMSE 为2.8820m.经过卡尔曼滤波后，定位精度有了很大的改善，CHAN 算法的RMSE 为1.0884m，Taylor 级数展开算法的RMSE 为0.6076m，顾及接收机与基站时间差的LLOP 算法的RMSE 为1.1242m.特别是Taylor 级数展开算法，经过卡尔曼滤波后的精度达到了亚米级，可以满足一般的室内动态定位需求.

3 结语

本文使用5G 毫米波观测值，通过基于TDOA 的算法完成了室内静态和动态定位，并与参考值进行了比较，验证了三种不同的5G 室内定位算法的能力.实验表明，在室内静态定位时，效果最好的是CHAN 算法，定位精度为0.2856m；室内动态定位中，效果最好的是Taylor 级数展开算法，定位精度达到了亚米级；另外，顾及接收机与基站时间差的LLOP 算法可以在计算复杂度更小的情况下，快速完成相对较好的定位结果，有利于实时应用.将来，考虑使用GNSS 原始观测值，与5G 观测值进行融合处理，实现室内外的无缝定位.

致谢：感谢国家授时中心武建锋老师课题组提供的数据.本文的研究得到了国家自然科学基金项目(41674034,41974032)和中组部、中科院高层次青年人才项目，以及王宽诚教育基金会的支持.