基于接收机钟差约束的精密单点定位时间传递研究

赵传宝，盛传贞，张宝成

(1.卫星导航系统与装备技术国家重点实验室，石家庄 050081；2.中国科学院精密测量科学与技术创新研究院，武汉 430000；3.中国科学院大学，北京 100000)

0 引言

精密单点定位(PPP)是一种能够利用单台接收机的测码伪距和载波相位观测值并借助外部高精度轨道钟差产品进行绝对定位的技术[1].PPP 技术起初主要应用于精密位置确定等应用，后来张宝成[2-3]提出了非组合PPP 模型，该方法开始逐渐广泛应用于电离层、对流层等空间大气的研究.2016 年PPP 技术开始逐渐应用到时间传递领域[4].国内外相关学者均对PPP 授时与时间传递进行了深入地研究[5-6].作为一种全视方法(AV)，由于PPP 可以利用测站处可观测到的全部卫星数据，因此时间传递性能不会受两测站间距离长短的影响，具有更高的灵活性[7-9].目前，国际计量(BIPM)已将PPP 作为国际原子时(TAI)主要的例行时间传递技术之一[10].

随着氢原子钟的不断普及，越来越多的监测站配备了氢原子钟作为外部高精度时间频率基准.氢原子钟相对于铷、铯等原子钟具有更高的稳定性[11-12].但是在传统的PPP 时间传递数据处理中通常将接收机钟差参数视为白噪声(WN)进行处理，这在一定程度上浪费了氢原子钟的高稳定性信息.为了充分利用氢原子钟高度稳定的特性，本文通过20 个全球分布的国际GNSS 服务(IGS)测站，90天的GPS 观测数据基于Hadamard 方差得到了经验的氢原子钟方差特性，并在PPP 解算中将相邻两历元的接收机钟差参数约束为随机游走模型进行处理，从而提高PPP 时间传递性能.为了验证本文提出的基于接收机钟差约束的PPP 时间传递方法，选用IGS AMC4、GODE、USN7、BRUX 四个测站的GPS 观测数据并构成AMC4-BRUX、GODE-BRUX、USN7-BURX 三条时间链路进行时间传递稳定性分析.

1 接收机钟差约束的PPP 模型与时间传递方法

1.1 PPP 时间传递原理

由于非组合PPP 相比于消电离层组合PPP 保留了更多的原始信息且不会增大观测值噪声，因此本文基于非组合PPP 模型进行时间传递.其原始观测值的观测方程[13-14]如式(1)：

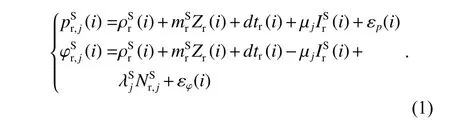
式中：和分别为第i个历元卫星S到 接收机r 在频率j上的伪距与相位观测值；(i)为卫星与接收机间的几何距离；Zr(i)和mSr分别为测站天顶对流层延迟与投影函数；dtr(i)为接收机钟差；(i)为第一频率上的斜电离层延迟；µj=(λj/λ1)2,(j=1,2)为与频率相关的系数；和分别为j波段的波长与模糊度；εp(i)和εφ(i)分别为伪距与载波观测值中观测噪声、多路径等未建模误差.

对于传统的PPP 时间传递方法，接收机钟差参数dtr(i)通常在滤波过程中被当作WN 参数处理(即不进行历元间的传递)，而本文针对以氢原子钟提供时间频率为基准的测站，将接收机钟差参数建模为随机游走模型.具体过程为：1)将第i个历元接收机钟差的估计值dtr(i)作为第i+1个历元接收机钟差的预报值；2)将第i个历元接收机钟差估值的方差加上一定的过程噪声σrclk作为第i+1个历元接收机钟差预报值的方差，其中采用的接收机钟差的过程噪声σrclk为事先经过大量测站解算得到的经验方差；3)重复步骤1)和步骤2)进行滤波解算.

1.2 氢原子钟经验方差计算

为了充分利用氢原子钟的高稳定性，本文将历元间的接收机钟差约束为随机游走模型.氢原子钟先验方差σrclk计算方法如下：1)首先利用静态PPP 逐天逐站处理20 个外接氢原子钟的IGS测站数据，并将接收机钟差参数视为WN 参数处理得到多个接收机钟差序列；2)考虑到氢原子钟的频率漂移影响，利用Hadamard 方差获取各测站接收机钟差序列的先验方差[15-16]，并取其均值得到氢原子钟钟差的过程噪声经验方差.

式中：σHDEV(τ)为使用一天的接收机钟差序列计算得到的Hadamard 方差；τ为数据采样间隔；c为真空中光速.

1.3 数据处理策略

在文中，由于重点关注接收机钟差参数在授时以及时间传递中的应用，因此在PPP 解算时，将测站固定为IGS 发布的测站坐标轴解值；对流层干延迟部分采用UNB3 经验模型进行改正，湿延迟部分作为待估参数并按照随机游走模型估计，投影函数采用全球投影函数(GMF)；接收机钟差参数作为随机游走参数进行估计；电离层斜延迟作为WN 参数估计；模糊度参数作为弧段常数估计.其他必要的改正，如天线相位中心改正、天线相位中心变化、相位缠绕等改正也均已考虑.

2 实验结果与分析

2.1 氢原子钟先验方差

基于2019 年第1—90天年积日20 个外接氢原子钟的IGS 测站得到的接收机钟差的Hadamard 方差序列如图1 所示.由图1 可知，不同方差序列之间的最大差异不超过2mm.所有测站90天的平均方差为1.9mm，标准差为0.23mm，因此不管是同一测站的不同天之间还是不同测站之间，先验方差序列都是较为稳定的.所以对于任何外接氢原子钟的测站，只要不发生钟跳、设备变更等问题，都可以将1.9mm 作为PPP 中氢原子钟钟差参数的随机游走噪声(RWN).

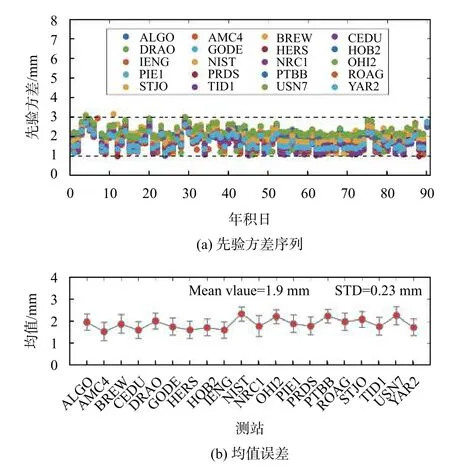
图1 氢原子钟测站先验方差序列

2.2 Hadamard 方差分析

首先，为了分析不同精密钟差产品对PPP 授时以及时间传递稳定性的影响，我们以AMC4 与BRUX 两个测站为例，采用WUM、GBM、COD、JPL 4 家IGS 分析中心产品分别进行授时和时间传递稳定性分析.图2 为基于上述4 家分析中心精密轨道钟差产品的PPP 授时频率稳定性.由于不同分析中心在钟差估计时选择的基准不同，卫星钟差中所包含的基准又会在PPP 解算时被接收机钟差参数吸收，因此卫星钟差产品中基准的稳定性会对PPP 授时稳定性产生一定影响.由图2 可知，使用WUM 与JPL产品可以获得更高的长期授时稳定性；使用COD 产品可以获得较高的中期稳定性，不同产品在短期授时稳定性方面差异不明显.

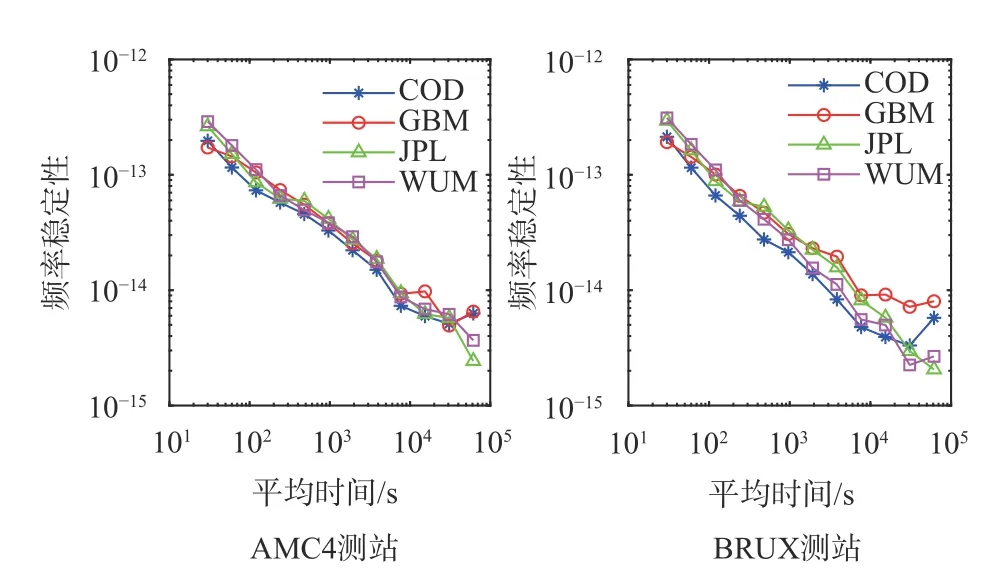
图2 基于四家分析中心精密产品的PPP 接收机钟差频率稳定性

在时间传递中，由于要将两站接收机钟差进行差分，因此包含在不同精密钟差产品中的基准会被消除，从而不再影响时间传递的性能.图3 为分析使用不同精密轨道钟差产品AMC4-BRUX的时间传递稳定性.可以看出，使用不同精密产品的时间传递稳定性具有较好的一致性，因此卫星钟差产品的基准不影响时间传递的稳定性.

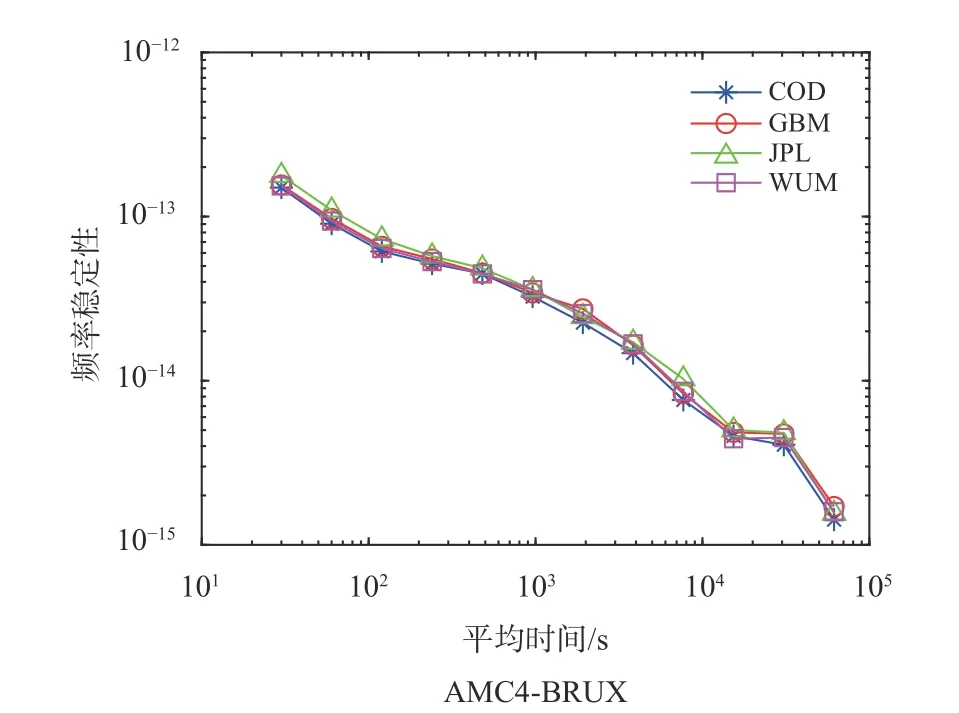
图3 不同精密产品时间传递稳定性

图4 为2019 年1 月1 日USN7-BRUX 时间链路的接收机钟差之差序列.其中蓝色线为传统的PPP 方法(PPP1 方法)得到的钟差时间序列，红色线为基于本文改进的附加接收机钟差约束的PPP 方法(PPP2 方法)的到的钟差时间序列.图5为2019 年1 月1 日USN7-BRUX 时间链路中钟差序列的历元间差分序列，可以看出，PPP2 方法得到的钟差序列明显具有更小的噪声，因此本文提出的PPP2 方法进行时间传递具有更高的稳定性.

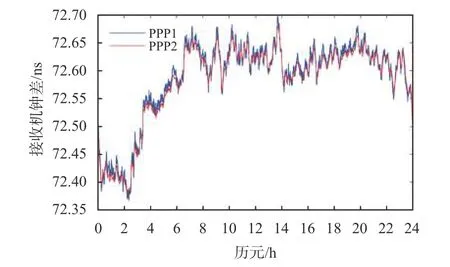
图4 2019 年1 月1 日USN7-BRUX 时间链路钟差之差序列

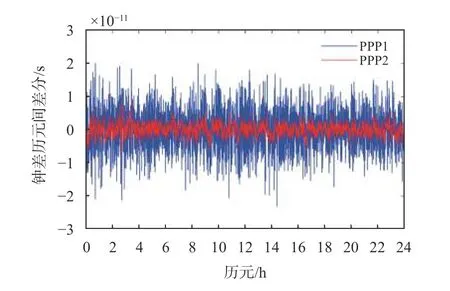
图5 2019 年1 月1 日USN7-BRUX 时间链路钟差历元间差分序列

为了从频率稳定性的角度验证本文提出的方法在时间传递中的性能，我们分析了AMC4-BRUX、CODE-BRUX、USN7-BRUX 三条时间链路在2019 年第1—7天年积日的PPP 接收机钟差的时间序列的Hadamard 方差，其结果如图6 所示.结合图6 可知，基于接收机钟差约束的PPP 时间传递相较于传统的PPP 时间传递具有更高的频率稳定性.其中，本文提出的方法在短期稳定性方面提升最为明显，可以实现量级上的提升.虽然对于中长期的稳定性提升没有短期稳定性显著，但是基于接收机钟差约束的PPP 时间传递方法在时间传递稳定性方面始终优于传统的PPP 时间传递方法.

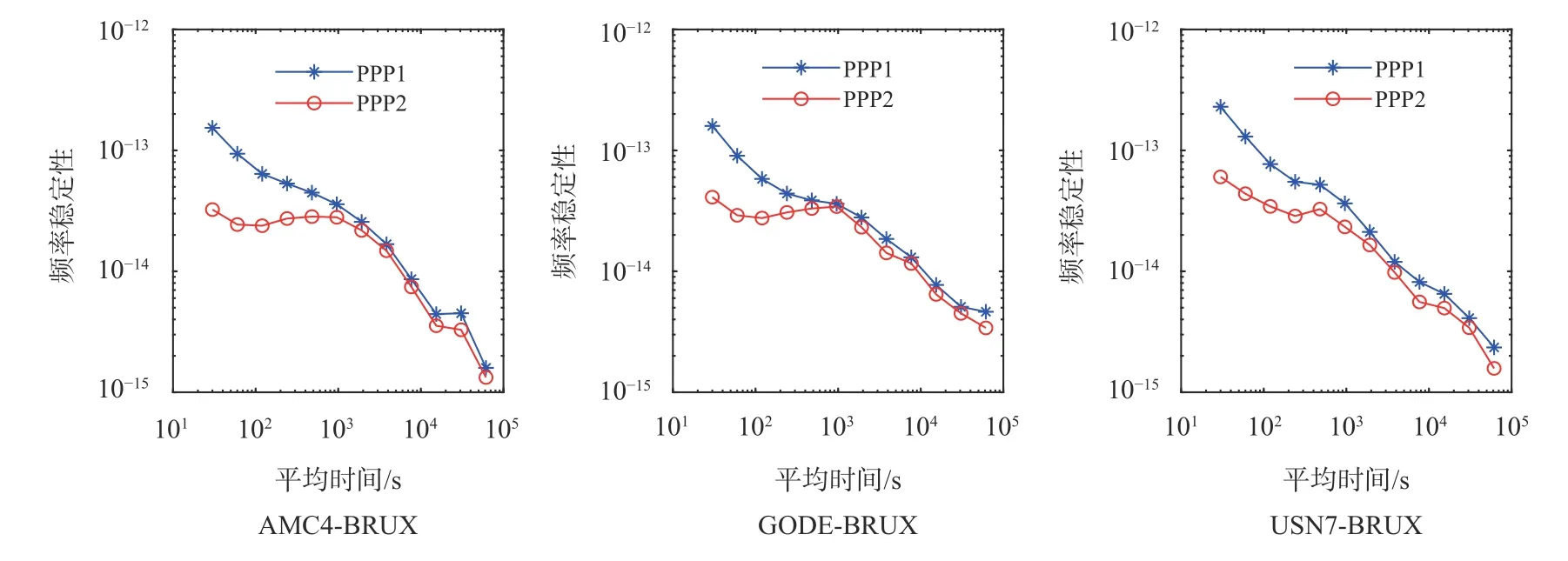
图6 三条时间链路频率稳定性对比

3 结束语

基于20 个全球分布并配备高精度氢原子钟30s采样间隔的IGS 测站数据利用Hadamard 方差得到了氢原子钟的经验方差为1.9mm，并在PPP 时间传递中将相邻两个历元的接收机钟差约束为随机游走模型.通过实验可知：1)不同精密卫星钟差产品中的基准会对单站接收机钟差频率稳定性产生一定影响，但对于时间传递来说，由于其基准可以通过测站间差分被消除，因此卫星钟差中包含的基准不影响时间传递的频率稳定性；2)对外接氢原子钟的接收机钟差经过约束后在短、中、长期稳定性方面均有提升，其中短期稳定性更为明显，可以实现量级上的提升.