高中数学“一题一课，多解变式”教学模式探究

李丽萍

(贵州省黔西第一中学 贵州 黔西 551500)

2014年，国家教育部在《关于全部深化教育改革，落实立德树人根本任务的意见》中提出了“核心素养”这一概念。之后，各地区的教育专家都纷纷开始了对核心素养这一教育理念的探究。也正是在这样的背景下，吕传汉教授提出了“一课一题，多解变式”的高中数学教学模式，指在每节课的教学中，从一道例题出发，通过一题多解、一题多变和一题多说的方式让学生掌握所有的知识内容。特别是在高三的复习课中，这种方式一方面可以减轻学生的课业负担，节约教育成本，另一方面还能够帮助学生理解和巩固所学的所有知识内容，提升解题能力。[1]下面，我们将以三角函数教学问题，具体分析高中数学“一题一课，多解变式”教学模式的实施方式。

1.题目呈现

在复习课中，学生掌握了基本的知识体系，所以很快就能够得到答案。

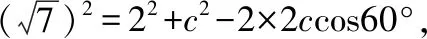
案例分析：解决这道题目的关键就是要熟练掌握正弦定理和余弦定理，对于高三的学生来说难度并不大。在解题完成之后，教师可以让学生思考以下两个问题：1.本题解题过程中考察了哪些知识内容？2.三角形六个元素，知道其中几个元素求，应该怎样计算另外几个元素？其中所包含的定理有哪些？通过这样两个问题，学生对三角函数部分的概念以及基本内容有了基本的回顾，为之后解决变式问题提供了保障。

2.变式探究

变式1：改变题目的所求内容

求(1)△ABC的面积

(2)试判断三角形的形状

(3)求BC上的中线长

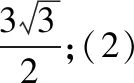
变式分析：这道变式题目改变了原案例中的所求内容，通过对这一题的分析和求解，学生将会更加深入的把握三角函数相应知识的应用方法。

变式2：改变题目中的已知条件

解题方法1(边化角)

解题方法2(角化边)

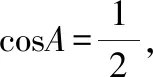
解题方法3(向量投影)

从向量投影的概念出发，ccosB+bcosC=a，所以2cosA·a=a

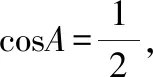
变式分析：在解决变式2的过程中我们采用了一题多解的方式，以此拓展学生思维，让他们将自己所掌握的知识实现灵活的转变。当然，对于一题多解的题目来说，究竟在解题过程中我们应该选择哪种方式不能一概而论，既要考虑到学生对知识的理解吧把握情况，又要考虑到实际案例中的应用过程。在本案例中，教师还可以继续改变a的取值，从而让学生继续求解三角形解的个数。

变式3：改变例题的条件或所求

解：通过方程思想可以得到方程组

3.反思感悟

当然，本道例题除了上文中所提到的内容之外，教师还可以继续进行深入，进行更多的变式设计。在这样的教学方式下学生可以从多个角度去思考问题，感受到数学知识的多边形，体会到各种数学思想与数学方法的渗透与应用。[2]当然，在这一教学过程中，教师也可以及时发现学生对知识掌握不够牢固的地方，及时让他们进行巩固，实现复习课的最终目标。总之，数学教师应善于通过“一课一题，多解变式”的方式让学生体会到一题多变、一题多解的过程，学会在解题过程中选择最佳的解题方法，获得最优的解题思路。