探图:小学数学高段“立体图形”复习课的学习策略

叶 贇

(浙江工业大学附属实验学校 浙江 杭州 310000)

1.“类比”猜想：归类图形，理空间体系

长方体是最基本的图形，其余立体图形在结构特征上与长方体其实是有内在联系的，因此在复习时通过互相点赞，梳理特征脉络；点到面再到体的图形想象，丰富立体层次；课件动态呈现，发展学生空间思维。

1.1 互相点赞，明特征脉络。萧伯纳曾说“交换思想，我们每个人将会有两种甚至更多思想”。为此笔者让学生自主梳理立体图形特征知识，并进行相互点赞学习，利于学生共同进步。

学生对立体图形的特征知识进行有序整理，让学生在梳理特征知识的过程中，思维得到发散，体会立体图形之间的内部联系；同时将作品展览于成果墙，让孩子体验来自同学的赞赏，激发学习兴趣。

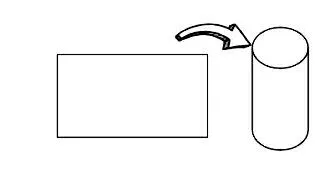
1.2 图形想象，丰立体层次。由体到面，再由面到体，学生的空间观念得到进一步发展，从不同角度研究立体图形，丰富学生对立体图形概念的理解，提升学生的数学思考能力。

通过一张长方形纸将平面与立体建立关联。通过长方形与圆柱之间的关联，让学生想象体的形成过程，引导学生学会观察、善于表达，多维感知面与体间的对应联系，让面与体的关联更紧密，从而丰富学生的空间思维。

2.“转化”推理：剖析图形，展空间想象

探究立体图形表面积，实则体转化为面的关系。为此复习时精心选择教学素材，让立体联系更加紧密；转化图形，让面体沟通更顺畅；融会实践，能够帮助学生内化立体知识，显著提高复习课的增量。

2.1 精选素材，紧知识联系。复习素材的精心选择是复习课成功的关键要素。由此笔者选择了直观且贴近学生生活实际的素材，这有利于学生更好的理解知识。

教师从一张纸出发，设计立体图形面积复习将一张长方形纸作为复习素材极其简单，不仅将长方形与直角三角形进行了有效沟通，同时也将面与体进行了充分联系，让面与面、面与体、体与体之间的联系更加紧密，实现了复习课的“密度”，提升学生思维能力。

2.2 转化图形，顺面体沟通。巧妙的利用素材，可以使复习课不仅“温故”，还可以“知新”，让零散单一的立体知识融为一体，实现知识的增值，达到“知新”的复习成效。

在探究粉笔表面积时，学生用长方形包在粉笔外面，把粉笔的曲面转化成求长方形的面积，通过转化的方法，让学生再一次深刻感悟立体图形表面积与长方形之间的关联，拓展了学生的空间思维。

3.“逆向”推导：验证公式，强空间观念

知道公式的几何意义是学习立体图形体积知识的重点。为此笔者通过微课重温体积的知识点，借助逆推的方法让知识串起来，寻找知识的本质。同时注重应用，让数学知识服务于生活。

3.1 微课重温“知识点”。体积复习的微课能够让学生快速重温立体图形体积的知识，唤醒学生已有经验，直观生动的视频方式更能抓住学的注意力，从而有效达到知识点的回顾。

师：回顾立体图形的体积我们是怎样得到的？

生1：通过转化法，把圆柱转化成一个长方体来计算。

生2：通过实验法，把圆锥装满水导入同底等高的圆柱中，正好倒3次。

通过微课的方式，让学生回顾重要的“知识点”，明确已经学习的立体图形体积计算公式，再现体积推导过程，让学生对体积知识形成系统性，找到本质联系，为后续教学打好基础。

3.2 逆推清晰“知识源”。数学知识不是碎片化的，割裂的。在模块化学习中，让学生在逆推对比中串联知识，建构统一的立体图形体积数学模型，让学生清晰立体图形体积的知识源。

师生共同整理出直柱体特征教学片段

师：长、正方体、圆柱这些图形可以通过平移得到，那其他图形呢？

生1：看作一个三角形向上平移得到，三角形就是这个三棱柱的底，向上平移的距离就是高。

生2：也可以用底面积乘高计算，因为都是通过图形平移得到的

师：如果变成五边形，n边形，体积怎么算？生4：还是底乘高。

师：像这种立体图形，我们把他叫做直柱体。(板书：直柱体)

学生通过讨论和交流，提取出直柱体的共同特征，就是都可以用底面积乘高来计算体积。由常见立体图形推广到n边形，这样的设计学生空间想象力得到发展，知识间的联系更紧密，同时落实知识点到面的过渡。