食饵具有避难和强Allee效应的时滞捕食者-食饵扩散模型研究

焦淑云

（1.山西师范大学 现代文理学院，山西 临汾 041004；2.山西师范大学 数学与计算机科学学院，山西 临汾 041000）

0 引言

在自然生态系统中，猎物和捕食者总是在运动，因此在描述生物和生态问题时，许多学者都用到了反应扩散方程[1-3]。 此外，时间延迟在种群模型中广泛存在。当捕食者吃掉猎物时，它不会立即增加捕食者的密度。存在妊娠期延迟，捕食者密度在一定时间后增加，这种类型的时延经常被学者研究[4-7]。在长期的生物进化过程中，物种会对周围环境做出反应。也不是所有食饵都参与到了交互过程，一些小的或相对机灵的猎物会躲起来以避免捕食者的攻击。为描述这种行为，许多学者研究了具有食饵避难行为的捕食模型[8-10]。对于一些物种，当人口密度低于这个阈值，物种将灭绝，这种现象被称为强Allee效应，具有Allee效应的模型也被许多学者大量研究[11-14]。

1 模型简介

本文综合考虑以上因素，建立了一类食饵具有避难和强Allee效应的时滞捕食者-食饵扩散模型，模型如下：

这里，u=u(x，t)和v=v(x，t)分别表示t时刻位于x的食饵和捕食者的密度，m∈(0，1)表示Allee效应阈值，θ∈(0，1)表示避难食饵的比例，α是最大捕食率，h表示半饱和常数，β代表转化系数，r为捕食者的死亡率，d1，d2表示食饵和捕食者的空间扩 散 系 数 ，u(t-τ)=u(x，t-τ)，v(t-τ)=v(x，t-τ)，τ表示猎物的生物量转化为捕食者的生物量需要的时间，n表示外法向量，Ω⊂Rn表示具有光滑边界∂Ω的有界域，本文我们取Ω=(0，l)。

对于不含扩散、时滞及强Allee效应的模型（1），Kar等[15]研究了模型的有界性、平衡点的稳定性以及极限环的存在性。对于具有强Allee效应和Beddington-De Angelis功能反应函数的时滞扩散模型，Liu等[16]在稳定状态分析了模型正平衡点的稳定性对时滞大小的依赖关系，得到了Hopf分支发生的条件，并利用正规型理论和中心流形定理进一步分析了Hopf分支的方向和稳定性。但据我们所知，综合考虑食饵避难、强Allee效应、时滞和空间扩散模型尚未有人研究。本文综合考虑这些因素建立模型，分析模型（1）的动力学行为，并讨论时滞和空间扩散对模型动力学的影响。

本文的布局如下：在第2节中，讨论只有扩散的简化模型的动力学行为。在第3节中，以时滞τ为分支参数，分析模型（1）相应的特征方程，研究空间Hopf分支的存在性。第4节提供了一些数值模拟来说明理论分析结果，文章最后给出总结。

2 不含时滞模型的动力学行为

3 时滞模型的动力学行为

4 数值结果

为了验证结果，本节根据先前的理论利用Matlab软件进行数值模拟，采用差分法和欧拉近似法，在零通量的边界条件下，考虑Ω⊂R，在这些数值模拟中，设置时间步长Δt=0.05，空间步长Δx=0.1，参数值设为 α=0.65，θ=0.25，β=0.58，h=1.175，r=0.15，m=0.1，d1=1，d2=2。利用上述参数容易算得：

由定理1可知，对于不含时滞和扩散的系统（1），E0是一个稳定的结点，E1，E2是鞍点，E*是局部渐近稳定的结点或焦点，数值模拟结果见图1。

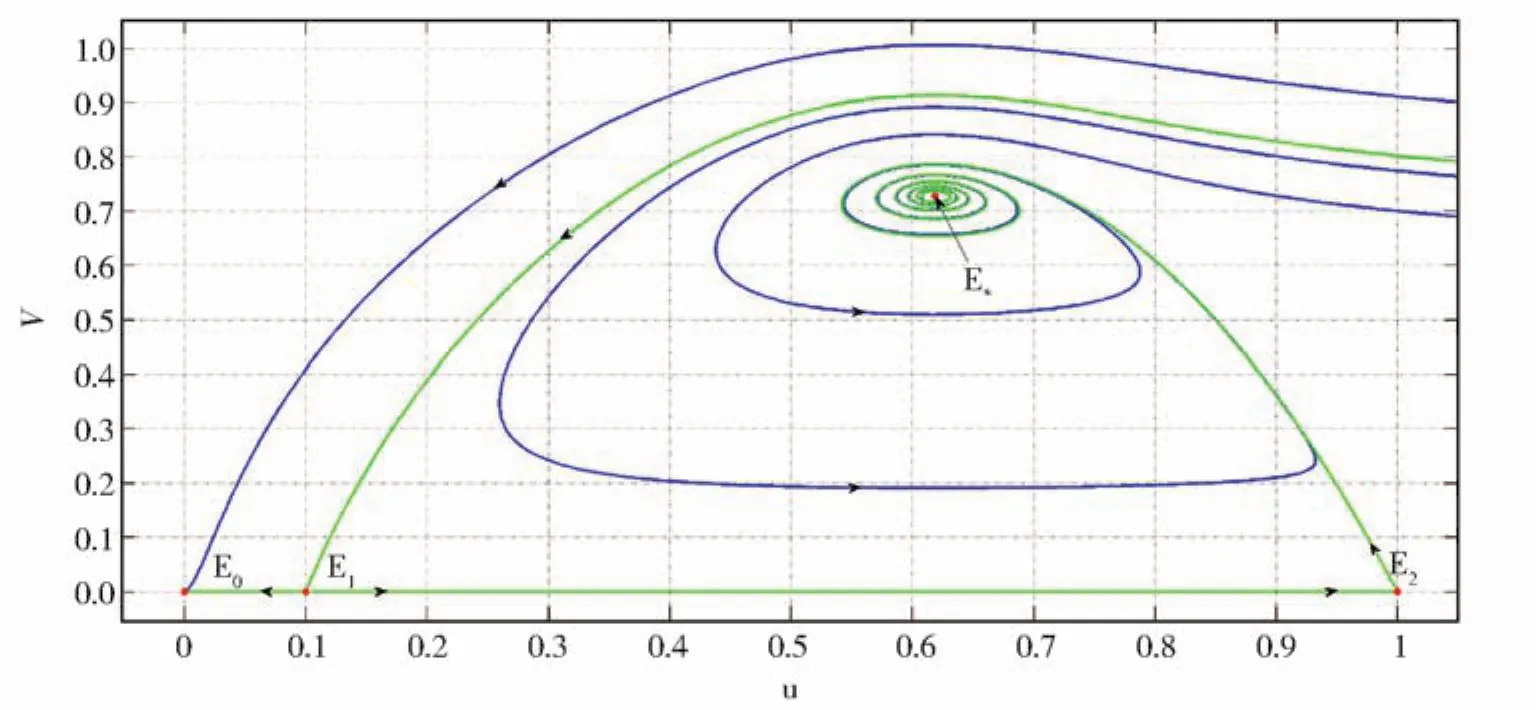
图1 模型（1）不含时滞和扩散时的相图蓝色曲线表示解轨线，绿色曲线表示鞍点的稳定和不稳定流形，平衡点用红色粗点表示Fig.1 Phase diagram of mode（1）without delay and diffusion.Blue curve represents solution trajectory，green curve represents the stable and unstable manifolds of the saddle points，and the equilibrium point is represented by the red thick point

进一步可得τ*=1.0511，由定理3知平衡点E*=(u*，v*)在τ∈[0，1.0511)时 渐近稳定，在τ∈(1.0511，∞)时不稳定；当τ=τ(j)k时，模型在正平衡点E*=(u*，v*)处经历Hopf分支。 我们分别取τ=0.9，1.08，3.2，数值模拟结果见图2，图3，图4。

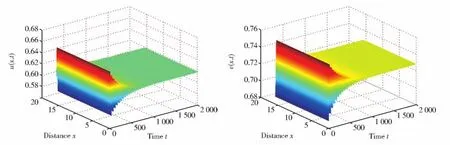
图2 当τ=0.9＜τ*=1.0511时，平衡点E*=(u*，v*)渐近稳定左图表示食饵种群密度u(x，t)，右图表示捕食者种群密度v(x，t)Fig.2 When τ=0.9＜ τ*=1.0511，the equilibrium pointE*=(u*，v*)is locally asymptotically stable.The left picture denotes the population density of preyu(x，t)and the right picture shows the population density of predatorv(x，t)

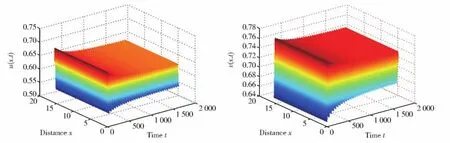
图3 当τ=1.08＞τ*=1.0511时，平衡点E*=(u*，v*)失稳，出现稳定的空间均匀周期解左图表示食饵种群密度u(x，t)，右图表示捕食者种群密度v(x，t)Fig.3 When τ=1.08＞ τ*=1.0511，the equilibriumE*=(u*，v*)tends to be unstable，and a stable spatial homogeneous periodic solution appears.The left picture denotes the population density of preyu(x，t)and the right picture shows the population density of predatorv(x，t)

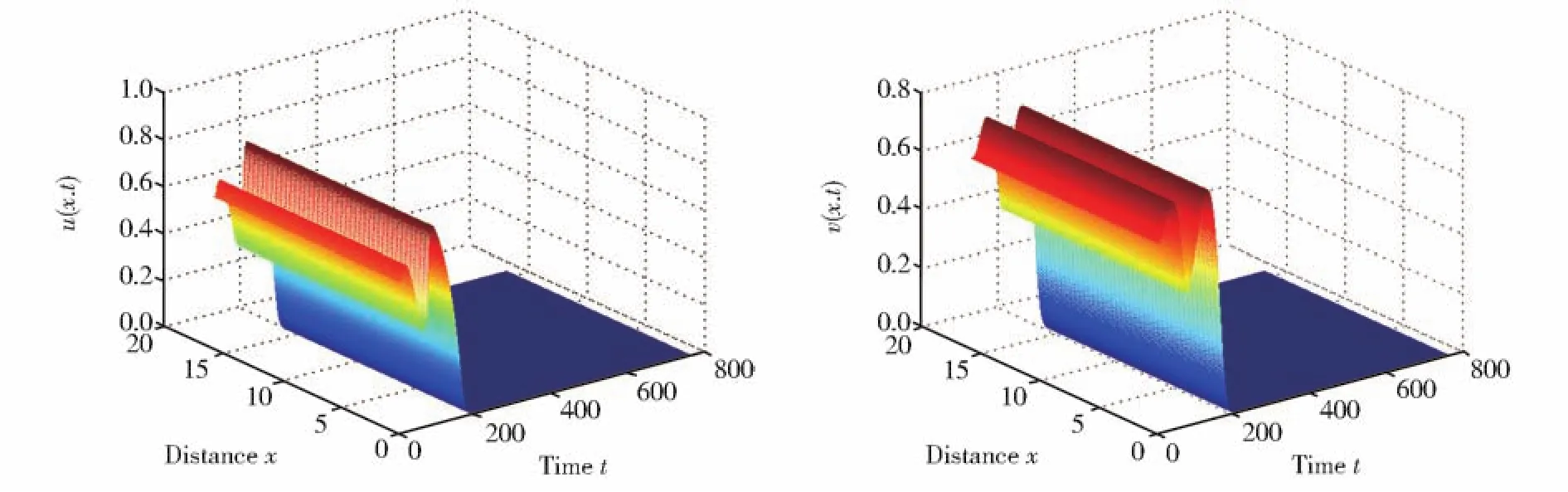
图4 当τ=3.2＞τ*=1.0511时，空间均匀周期解渐渐消失，两种群密度均趋于零左图表示食饵种群密度u(x，t)，右图表示捕食者种群密度v(x，t)Fig.4 Whenτ=3.2＞ τ*=1.0511，the spatial homogeneous periodic solution gradually disappears，and the densities of both populations tends to be zero.The left picture denotes the population density of preyu(x，t)and the right picture shows the population density of predatorv(x，t)

图2显示了当时滞比较小时（τ=0.9＜τ*=1.0511），平衡点E*=(u*，v*)的稳定性没有发生改变，仍然是渐近稳定的。 图3取τ=1.08＞τ*=1.0511，显示了当时滞略大于分支值τ*时，平衡点E*=(u*，v*)失稳，时滞引发了Hopf分支，出现了稳定的空间均匀的周期解。在图4中，取了较大的时滞值τ=3.2＞τ*，此时观察到捕食者和食饵种群密度趋于零，两种群均趋于灭绝。

5 讨论

本文考虑了一类食饵具有强Allee效应和避难的时滞捕食者-食饵扩散模型，在不考虑时滞和扩散的情况下，研究了模型解的存在性和有界性，得到了各平衡点的稳定性。对于共存平衡点，考虑了时滞和扩散对其稳定的影响，研究表明，物种的自扩散行为或较小的时滞不影响平衡点的稳定性，当时滞超过某一临界值时，共存平衡点失稳，此时从平衡点附近分支出一稳定的空间均匀周期解，对于给定的参数，当时滞较大时，捕食者和食饵趋于灭绝，这表明时滞对物种的生存起到负面影响。

本文的研究思想和方法可为同类模型的研究提供参考。由于篇幅有限，本文仅考虑了食饵具有强Allee效应和避难行为时滞扩散模型，在以后的研究中，将进一步根据实际情况考虑具有一般Allee效应、捕食者和食饵均具Allee效应以及具有分布时滞的捕食者-食饵模型。