具有信息干扰和Markov切换的随机传染病的灭绝性

王艳梅，刘桂荣

（山西大学数学科学学院，山西太原030006）

0 引言

近年来，数学模型已成为分析乙型肝炎、结核病等传染病发病机制的重要工具。此后，人们提出了各种种群动态的流行病模型[1-2]。众所周知，当传染病出现时，如何防治是人们关心的热点问题之一，而媒体报道和宣传活动能有效地预防和控制疾病的爆发。因此，信息干预（媒体报道、健康教育、心理暗示）作为一种非药物治疗是预防和治疗疾病的重要手段。目前关于信息干扰对疾病影响也存在许多研究成果[3-4]。文[5]研究了一类具有信息干扰的SIRS传染病模型并得到疾病灭绝和持久的条件。在实际中，传染病模型总是受各种环境噪声影响。基于此，许多学者对随机传染病模型进行了研究[6-9]。然而，生物系统还会受到电报噪声的影响，电报噪声描述的是传染病传播过程中在不同环境状态之间的切换，如气候的季节性变化等。进一步用Markov切换模拟电报噪声[10-11]。基于此，本文研究如下具有Markov切换的随机模型：

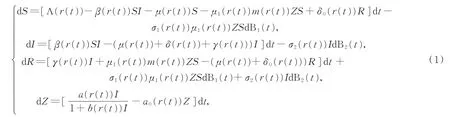
其中S、I、R、Z分别为易感者、感染者、恢复者和人群中信息密度；Λ为易感人口的出生或流入比率；γ，μ，δ，β分别为感染者的恢复率，自然死亡率，因病死亡率和接触传播系数；δ0为失去全部免疫力的比率；m和μ1分别为信息干预率和反应强度；a，b，a0分别为信息的增长率，饱和度常数和信息的自然衰减率。B(t)=(B1(t)，B2(t))是定义在完备概率空间(Ω，F，{Ft}t≥0，P)上的二维标准 Brown 运动，为

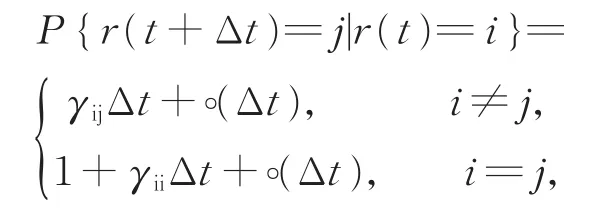
其中 Δt＞ 0，γij≥ 0（i≠j）表示从状态i到状态j的转移速率且假设 {r(t)，t≥ 0}是不可约的，从而存在唯一的平稳分布π=(π1，…，πN)满足线性方程πΓ=0且，πk＞0（k∈S）。对任意k∈S，Λ(k)，β(k)，μ(k)，μ1(k)，m(k)，δ0(k)，γ(k)，δ(k)，a(k)，b(k)，a0(k)，σ1(k)和σ2(k)都是正常数。

本文将讨论模型（1）全局正解的存在唯一性以及疾病灭绝的条件，同时分析噪声强度及Markov切换对疾病灭绝的影响。记，对任意定义在S上的函数g，记进一步给出如下记号：

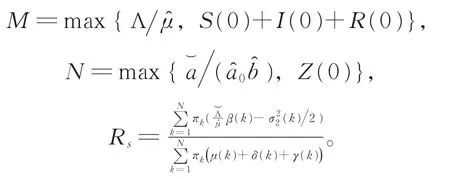
1 正解的存在唯一性

定理1对任意给定的初值

模型（1）在[0，∞)上存在唯一全局正解，即对任意的t≥ 0，(S(t)，I(t)，R(t)，Z(t)，r(t))∈R4+×Sa.s。

证明易知模型（1）的系数满足局部Lipschitz条件，则由文[12]中的定理3.15知，对任意给定的初值，系统存在唯一局部解(S(t)，I(t)，R(t)，Z(t)，r(t))，t∈[0，τe)，其中τe为爆破 时刻。下面证明τe=∞a.s.由于则存在充分大的n0，使得S(0)，I(0)，R(0)和Z(0)均属于[1n0，n0]。 对任意正整数n≥n0，令停时

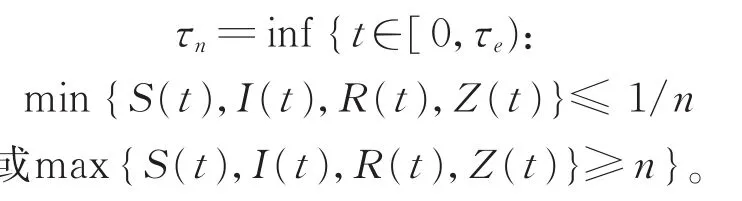
由（2）易知S(t)+I(t)+R(t)≤M且Z(t)≤N。定义C2-函数

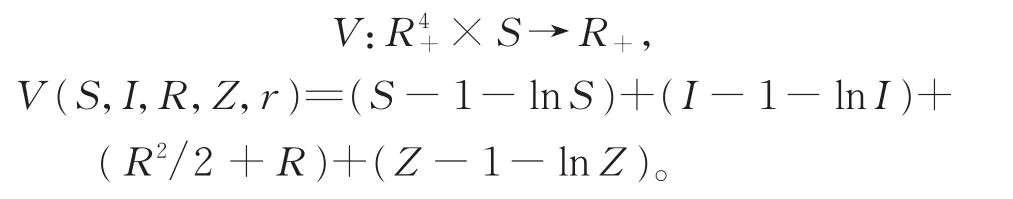
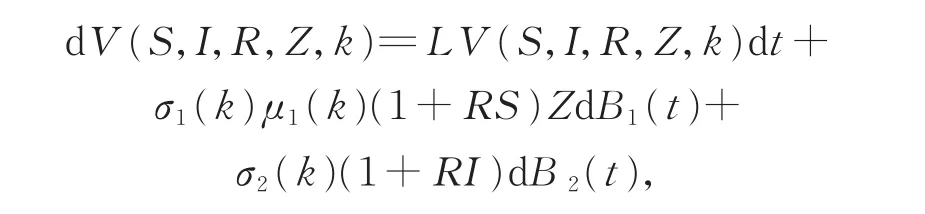
2 疾病的灭绝性

3 数值模拟

本节通过下面的例子来说明白噪声和Markov切换对疾病的影响。

例在（1）中取(S(0)，I(0)，R(0)，Z(0))=(2，1.2，0.8，0.5)和N=2。令

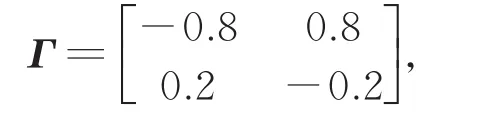
则其唯一的平稳分布为π=(0.2，0.8)。 取模型（1）中参数为。 若当状态空间只有状态1或状态2时，由计算分别可得或。由文[8]中的定理3.1可知疾病灭绝（参见图1）。若当状态空间有两个状态时，计算可得Rs≈0.321＜1。于是由定理2可知疾病灭绝（参见图2）。从图1和图2可以看出噪声强度及Markov切换对疾病灭绝速度的影响。

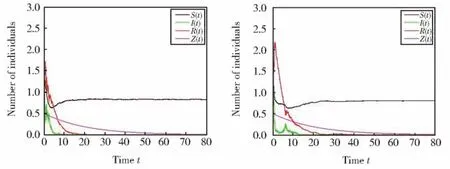
图1 状态空间只有一个状态时随机模型（1）的解Fig.1 The trajectories of stochastic model（1）for one state

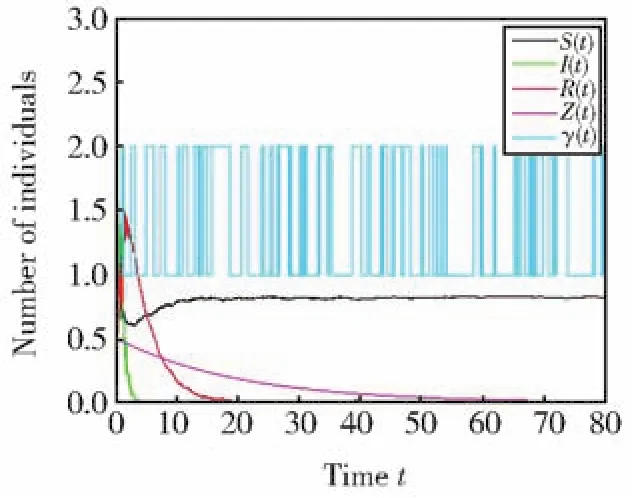
图2 状态空间有两个状态时随机模型（1）的解Fig.2 The trajectories of stochastic model（1）for two states

4 结论

本文研究了一类具有信息干扰和Markov切换的随机传染病模型，得到模型（1）存在唯一的全局正解。进一步，若Rs＜1，利用马尔科夫链的遍历性和局部鞅的大数定理得到了疾病的灭绝性。若状态空间只有一个状态且噪声强度为零时，则定理2改进了文[5]中的相应结果。若状态空间只有一个状态时，则能得到文[8]中定理3.1。此外，图1和图2表明噪声强度及Markov切换对疾病的灭绝产生影响。