基于自适应阈值模型的BDS-3周跳探测方法*

李送强，赵兴旺

（安徽理工大学空间信息与测绘工程学院，安徽 淮南 232001）

北斗三号全球卫星导航系统（BDS-3）在2020 年7 月正式开通，开始向全球用户提供高精度的导航定位信息。载波相位作为BDS-3 高精度定位的重要观测数据，在观测卫星的过程中信号受到多路径干扰、强电磁干扰、卫星振荡器停止等诸多因素的影响而产生周跳现象。即使一颗卫星发生1 周的周跳，也会导致定位结果偏差几厘米[1]。因此，周跳探测是利用相位数据进行高精度定位的首要任务。

常规的周跳探测方法有高次差法[2]、电离层残差法[3]、TurboEdit 方法[4]以及卡尔曼滤波法[5]等，但是各种方法都存在局限性，针对这些局限性已有大量改进方法被提出，这些方法主要集中在以下三方面。一是利用多项式拟合[6]、相位平滑伪距[7]、小波变换[8]等方法削弱组合中引入的伪距观测噪声。该类方法虽然降低了伪距中的噪声水平，但同时也引入了一些人为拟合误差、舍入误差等。二是通过历元间差分[9]、二阶无时差几何相位组合[10]、无几何无电离层组合[11]等方法降低电离层延迟影响，但是在探测一些电离层较活跃的数据时，此类方法要求有较高的采样间隔。三是建立自适应阈值模型[12]，该类方法对低采样率全球定位系统 （Global Positioning System，GPS）数据中含有的小周跳探测效果显著，但是目前针对自适应阈值应用在BDS-3 信号周跳探测的研究和分析还比较少。随着BDS-3 信号质量的提升[13]，建立一种适应BDS-3 信号噪声水平的周跳探测方法，提高周跳探测成功率，对于BDS 高精度数据处理工作具有重要意义。

本文根据BDS-3 的数据特征，对TurboEdit 探测法进行改进。首先，使用Melborne-Wubbena（MW）探测序列的均方根约束探测阈值，以避免噪声较大的伪距观测量影响探测效果。然后，针对无几何组合 （Geometry-Free，GF）探测阈值，使用高度角相关模型进行改进。最后，联合MW 和GF 探测，构建一种适用于BDS-3 信号的自适应阈值模型，并通过实测数据对模型的有效性进行验证。

1 传统TurboEdit 周跳探测算法

在BDS 进行定位时通过接收机观测卫星得到的观测方程为

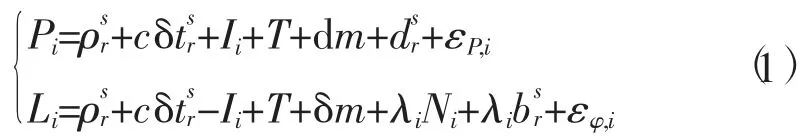
式中：Pi和Li分别表示频率i 上的伪距和载波相位观测量；为接收机r 到卫星s 之间的几何距离；c为光速；为接收机钟差和卫星钟差之和；Ii为与频率相关的电离层延迟；T 为对流层延迟；dm 和δm 分别为伪距和相位多路径延迟；分别为伪距和相位硬件延迟；εP,i和εφ,i分别为伪距和相位测量误差；λi为载波波长；Ni为整周模糊度。

合并与频率无关的误差项，忽略观测误差及电离层高阶误差项，多路径延迟和硬件延迟在历元间做差时可消除，所以不考虑，简化后的观测方程为

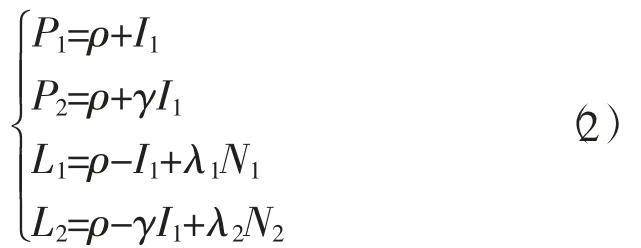
式中：ρ 包含了几何距离、对流层延迟、时钟延迟等与频率无关的误差项；为频率f1上的一阶电离层延迟放大系数。

为了探测出周跳，对式 （2）中的4 个观测方程进行线性组合，得到相应的周跳探测量，下面将介绍TurboEdit 法中包含的两种组合。

1.1 MW 组合周跳探测

根据MW 组合算法思想[4]，伪距和载波相位观测量的组合形式为

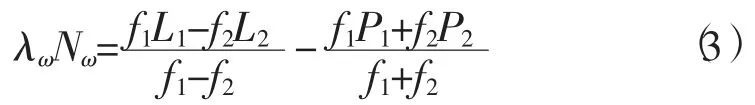
式中：λω=c/（λ1-λ2）为组合波长，c 为光速，λ1和 λ2分别为频率f1和f2的载波波长；Nω=N1-N2为组合整周模糊度。令 φω=φ1-φ2为 MW 组合载波相位观测值，其中φ1，φ2为载波相位观测值，将其带入式（3）得到MW 组合的周跳探测量为

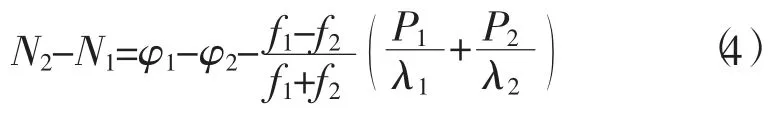
为了探测某一历元是否发生周跳，需要构建合适的阈值对探测量进行检测。传统的阈值通过式（5）和式 （6）不断递推计算获得。

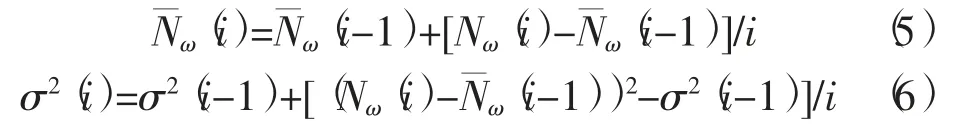
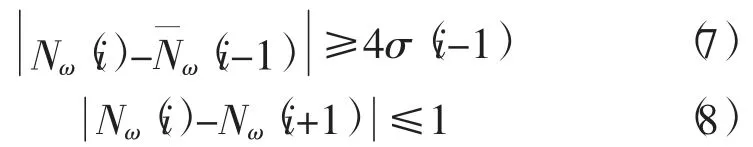
综上所述，MW 组合引入了误差较大的伪距观测值。一方面，降低了周跳探测精度，根据误差传播定律，如果伪距观测精度为0.3 m，则其探测精度约为1 周，实际操作中受人为或环境等因素的影响，伪距的精度要低于此，所以MW 组合通常只用来探测≥2 周的周跳。另一方面，在卫星刚进入视角时高度角较小、伪距噪声较大，如果把此时的数据加入中间观测弧段中求取周跳探测量，则会导致错判、漏判的现象发生。由式 （4）可知当两个载波上发生相同的周跳时MW 组合探测将失效。

1.2 GF 组合周跳探测

伪距相位GF 组合公式为

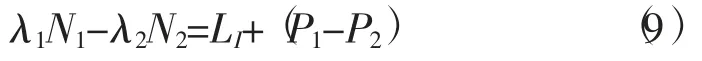
式中：LI=φ1λ1-φ2λ2，为无几何相位组合。

由于伪距不具有整数周期连续性且有约0.3 m的噪声影响，所以需要对P1-P2的结果进行拟合，又因为伪距多路径与高阶多项式具有强相关性，所以使用经验公式 min[（N/100+1）,6]确定拟合阶数[14]，其中N 为历元数。用式 （10）计算得到GF 组合周跳探测量ΔLGF。

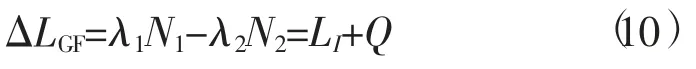
GF 组合探测条件见式 （11），如果式 （11）成立，则认为历元i 发生了周跳。

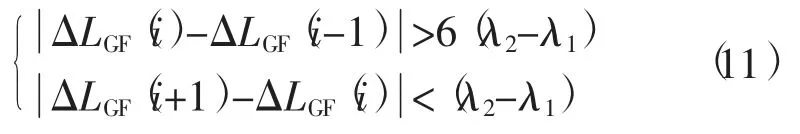
由上述可知，GF 组合同样引入了噪声较大的伪距观测值，使得在高度角较小时周跳探测精度下降，并且由式 （10）可知当两个频率发生的周跳大小的比值与两个频率对应波长的比值乘积为1 时，GF 组合探测将失效。

2 自适应阈值模型构建

由上述分析可知MW 组合和GF 组合周跳探测算法均存在弊端，本文为了消除或降低这些弊端带来的影响，建立一种适应BDS-3 信号噪声水平的周跳探测模型。一方面，对MW 组合法建立基于滑动窗口的均方根相关自适应阈值模型，对GF 组合法建立高度角相关的自适应阈值模型。建模分析的数据为武汉站 2020 年 7 月 6 日到 2020 年 8 月 4 日的观测数据，采样间隔为30 s。另一方面，针对两种组合有不敏感周跳的问题，使用两种组合联合探测的方法解决。

2.1 MW 组合自适应阈值

MW 组合在高度角较小时包含较高的噪声，通过使用滑动窗口的方法可以有效降低高噪声数据对中间历元周跳探测的干扰，具体做法是用式 （12）替换式 （5）和式 （6），每次只用窗口内的数据计算均值和均方根值，窗口逐历元往后滑动。

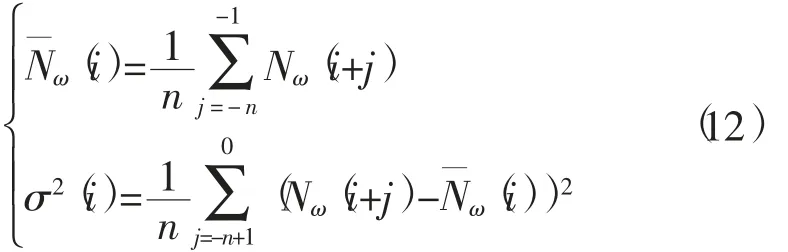
式中：n 为滑动窗口宽度，本文取20 个历元，其余变量含义与上文相同。

为了适应滑动窗口需要，根据式 （12）构建新的周跳探测量D，具体计算公式为

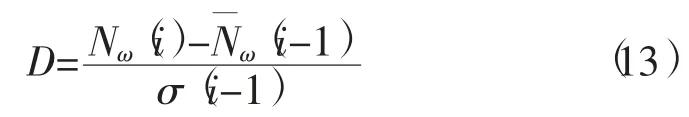
选取 2020 年 8 月 2 日 BDS-3 的 3 种轨道卫星无周跳的一段双频观测值序列，按照式 （13）计算MW 组合周跳探测量D 值序列，并以k0为阈值，结果见图1。

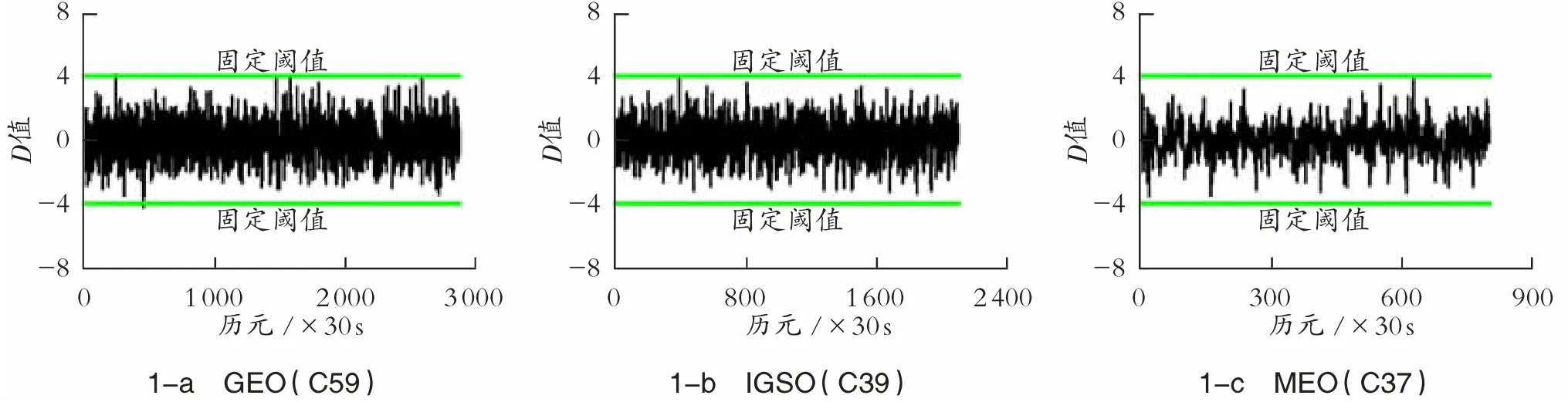
图1 MW 固定阈值与无周跳信号D 值序列图

从图1 可以看出，3 种轨道卫星的D 值均在-4～4 之间波动，其中地球同步轨道 （Geostationary Earth Orbit，GEO）卫星整体波动幅度较大，倾斜地球同步轨道 （Inclined Geosynchronous Orbit，IGSO）卫星次之，中圆地球轨道 （Medium Earth Orbit，MEO）卫星最小，且GEO 卫星有4 个历元由于噪声过大导致D 值超过k0值，即出现周跳误探。对于单颗卫星的D 值，在连续观测时段内波动的幅值也不同，这与观测历元的噪声水平有关[12]。为了适用于BDS 的3 种轨道卫星，阈值的设定必须将观测数据的噪声水平考虑在内。因此，本文构建一种适合BDS-3 信号的自适应阈值模型，具体形式为

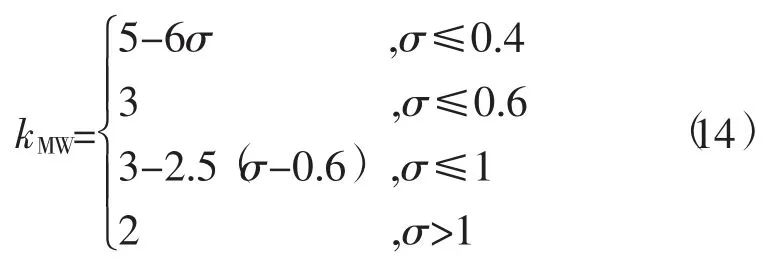
式中：σ 为通过式 （12）计算得到的均方根值。

2.2 GF 组合自适应阈值

为了探究GF 组合周跳探测量、高度角、传统周跳探测阈值之间的变化关系，选取2020 年8 月2 日BDS-3 的3 种轨道卫星无周跳的一段双频观测值序列计算周跳探测量时间序列与高度角序列，传统周跳探测阈值一般取固定值5 cm，结果见图2。

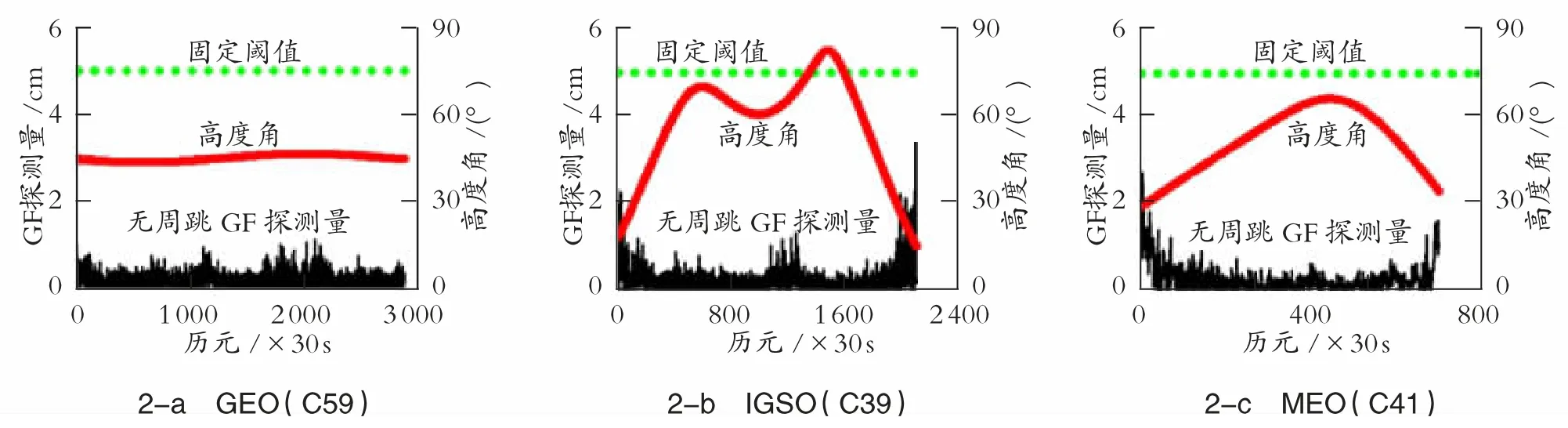
图2 GF 探测量与传统固定阈值及高度角变化关系图

从图2 可以明显看出，探测量在高度角较高时表现得较为平稳，在0～2 cm 之间波动，其中GEO卫星高度角较高且变化较小，所以其探测量的波动区间在3 种轨道卫星中也最小，在0～1 cm 之间。此外，当高度角低于35°时，探测量会急剧升高，如IGSO 卫星在1900 历元之后，高度角下降到30°以下，其探测量波动范围也随之从0～1 cm 上升到0～2 cm，有个别历元甚至超过3 cm。传统固定阈值选取的数值较大，避免了探测量波动较高的情况下出现周跳误探，但是固定阈值在低噪声的历元离探测量波动区间较远，容易出现周跳漏探。综上所述，GF 组合探测量与高度角具有相关性，且传统固定阈值不适合在高度角较高的历元中使用。因此，本文构建一种适用于BDS-3 信号的GF 组合周跳探测高度角相关阈值模型，具体形式见式 （15）。

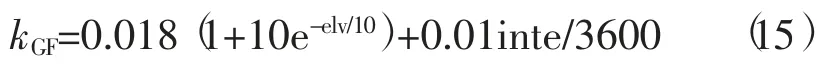
式中：elv 为高度角；inte 为数据采样间隔。

3 实验检测及结果分析

为了验证上述自适应阈值模型的有效性，使用武汉站在2020 年9 月5 日观测的 BDS-3 的3 种轨道卫星数据，采样率为30 s。观测时段内的数据已事先验证没有周跳，在实验过程中将人工添加一些周跳，具体添加周跳的大小及历元见表1。

图3 为加入周跳后的观测值序列按照MW 组合计算的探测量时间序列，结合第35 页表2 可以看出，使用自适应阈值探测结果基本符合上述分析，所有周跳组合中除了相等周跳组合以及GEO和MEO 数据中小于1 周的周跳未被探测出外，其他周跳组合在3 种轨道卫星数据中均被探测到，且没有出现误探。相比之下使用固定阈值，GEO 卫星数据中的第1081，1338，1839 历元将被误探。综上所述，使用自适应阈值的MW 组合法可以有效探测出BDS-3 信号中80%～90%的周跳，且较使用传统阈值降低了周跳误探率。

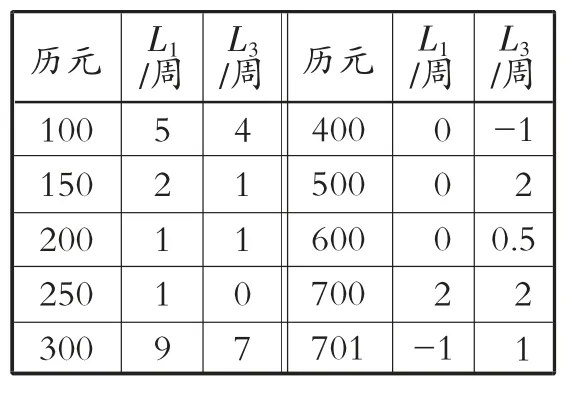
表1 插入周跳大小及历元

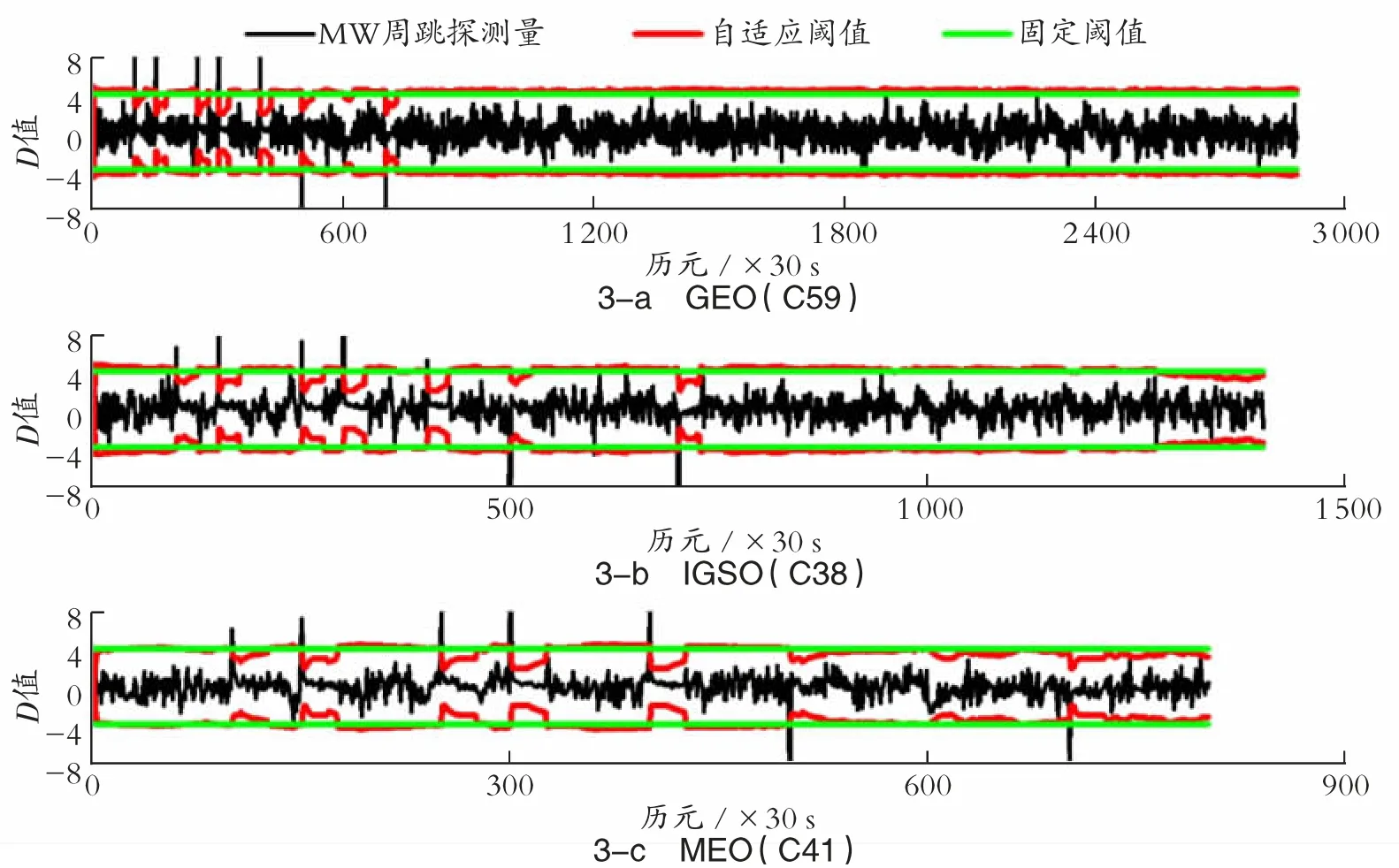
图3 加入周跳后MW 组合探测量变化曲线图

图4 为使用高度角相关模型计算的GF 组合自适应阈值序列以及加入周跳后的探测量序列。可以看出，自适应阈值序列较传统的固定阈值可以更好地符合探测量的变化趋势，更加贴近无周跳时间段的探测量序列波动上限，所以探测的精度也更高，避免漏探一些小周跳。尤其在噪声较大的历元，自适应阈值可以随GF 探测量序列波动区间上升而自适应增加，降低了周跳误探率。结合表2 可以看出，使用自适应阈值除了1.2 节推导的不敏感周跳组合无法探测外，其余周跳组合在3 种轨道卫星数据中均可以被探测到，而如果使用传统的固定阈值，周跳组合（1，1）将被漏探。综上所述，改进后的GF 组合周跳探测法探测成功率最低为90%，极大地提高了周跳探测精度。

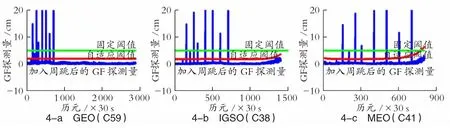
图4 加入周跳后GF 组合探测量变化曲线图

表2 为上述周跳探测实验结果的统计数据。可以看出，改进的MW 组合及GF 组合周跳探测法的探测成功率都在80%以上，均存在不敏感周跳，而TurboEdit 法联合了两种组合同时进行周跳探测，避免了使用单一组合出现不敏感周跳的问题，对BDS-3 的3 种轨道卫星观测数据中周跳的探测成功率达到100%。综上所述，本文改进的TurboEdit 法对于BDS-3 观测数据中的周跳探测切实有效。

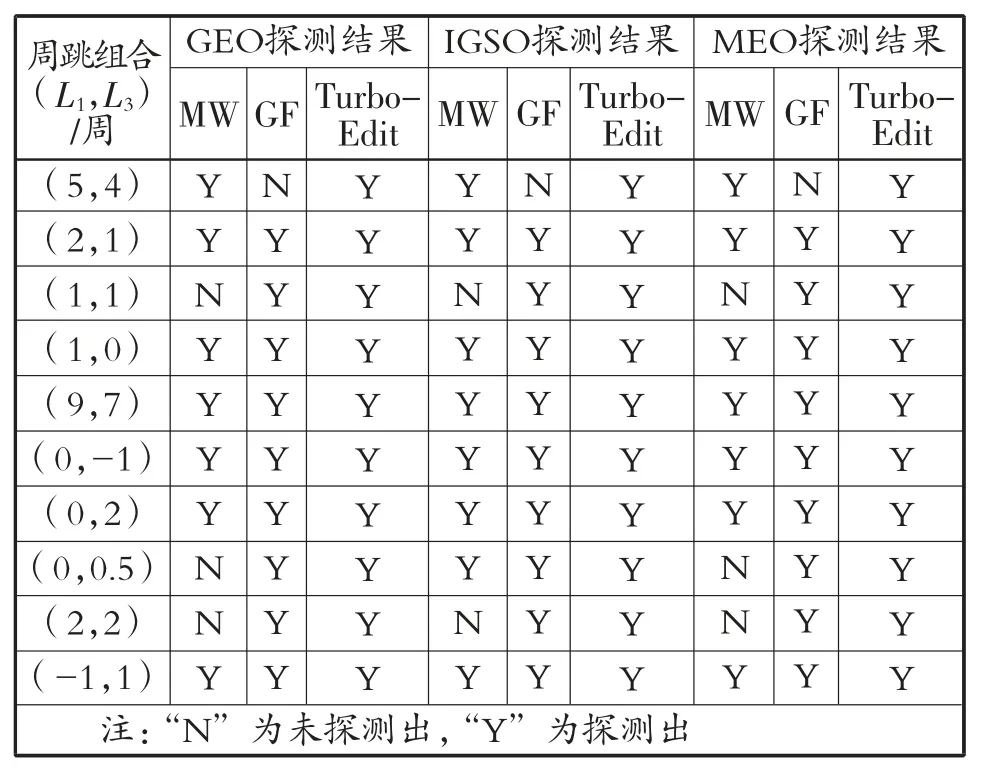
表2 使用自适应阈值周跳探测结果

4 结论

本文分析了传统周跳探测算法存在的一些缺陷，在TurboEdit 法的基础上建立了周跳探测自适应阈值模型，并通过30 s 采样率的BDS-3 观测数据进行了验证。实验结果表明，使用本文建立的自适应阈值模型相较于传统的固定阈值，能显著降低MW 组合和GF 组合在噪声较大时的周跳误探率，提高两种组合对小周跳的探测性能。通过TurboEdit法联合两种组合同时探测，能够探测出绝大部分周跳，有效避免了使用单一组合出现不敏感周跳的问题，更好地适应了BDS-3 信号的周跳探测工作。