对解析几何中定点定值问题的一些思考

宗 蕾 (江苏省常熟市中学 215500)

解析几何是高考必考的内容，它通过研究空间与数量的关系，可以培养学生的直观想象、数学抽象、逻辑推理等素养．解析几何中曲线的性质常常以一些定点及定值问题的形式出现，比如证明动直线经过定点或计算某些量(如向量的数量积)是定值，在逻辑上体现了“动”与“定”的辩证关系，成为高考的热点问题．同时，由于这些问题一般计算量大、字母较多、方法灵活多样，也成为学生学习的难点．探索这类问题的多种解题方法，有助于提高学生解决问题的能力，提升学生的数学学科素养．

1 科学预设方法，提升运算效率

解析几何中“动”与“定”的辩证关系决定了解题的方法具有多样性.教师在课堂上要引导学生根据问题的条件和问题本身，设计好整个计算的方法，然后通过比较分析各方法的繁简，选择最优的方案进行求解，这样往往会事半功倍．

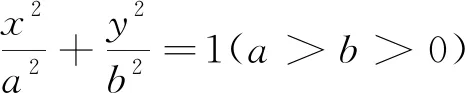
(1)求椭圆的方程；

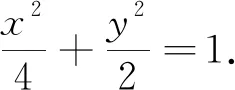
通过比较发现，方法1是利用斜率k为参数，需要求两个点的坐标，计算量比较大，过程比较复杂；方法2利用点M的纵坐标为参数，将一次的直线与两次的椭圆方程联立，只计算了一次，计算量小了很多；而方法3是两个一次的直线方程联立，计算量最小、效率最高．因此，方法3是本题最好的方法．

2 夯实常规技能，避免思维固化

解析几何的教学、特别是定点定值问题的教学，要注重常规经典方法的渗透，该“死算”的时候千万不能取巧走捷径．但是，事物都有其普遍性和特殊性，教师也要避免学生出现解法固化、思维固化的情形，即在过分强化某种解法后，学生可能出现不管什么问题都采用这种解法的情况，想利用一种解法“打遍天下”．这种情况下，一旦出现跟常见的情形不同的陌生情形，学生思维容易受阻，导致解题不顺畅．这应是我们在解析几何相关教学中尽量避免的情况．

(1)求椭圆C的标准方程．

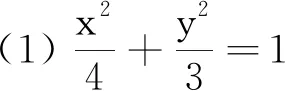
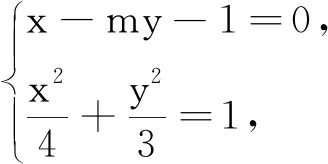
3 利用特殊设定，打开思维闸门

从特殊到一般是重要的数学思维方式．解析几何的定点定值问题，在很多时候可以借助特殊情形来猜测答案．比如在证明动直线过定点的时候，可以将动直线中的参数取两个特殊值，然后联立起来，解出的交点就是所求的定点；再比如求定值的问题中，可将直线或者圆特殊化，就能经过简单的计算得出答案．但是要注意，这样仅仅代表了一种特殊的情形，依然需要对此给出证明．

上面的解法就是采用了由特殊情形到一般情形的方法，计算量较小、易于掌握．

解析几何的定点定值问题作为高考的中档题，需要一定的计算能力．教师应该做到：(1)在课堂上给学生足够的时间去计算，避免学生“看题”代替“算题”，避免计算时浅尝辄止．课后作业的布置尽量少而精，以便给学生充裕的时间去独立计算．(2)加强过程评价，鼓励学生独立计算的精神，并及时纠正学生计算过程、方法的错误，对计算的关键点适当地剖析．(3)增加对作业中计算的评语，鼓励学生敢于计算、克服畏难畏繁的心理，增强学生“顽强计算”的意志和品格．