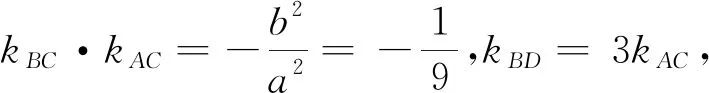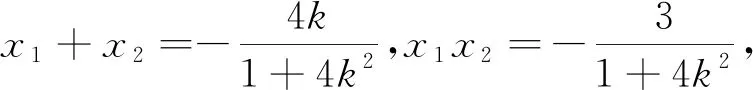溯“源”引“流” 挖掘本质 塑造模型——从2020年全国卷解析几何压轴题说起

徐 兰 (江苏省溧阳中学 213300)

高三复习课的教学是为了促进知识条理化、系统化，提高学生分析问题和解决问题的能力，形成良好的认知结构.圆锥曲线历来是高考中的重点、难点，其因点、线、曲线的错综复杂而易让学生望而生畏.笔者就2020年全国高考卷的圆锥曲线来谈谈高三复习课圆锥曲线的复习策略，溯源引流，对同根同源问题寻找试题的共性，把握问题的本质.

(1)求C的方程;(2)点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足．证明：存在定点Q，使得|DQ|为定值．

第(2)问：设M(x1，y1),N(x2,y2).

整理得(2k+3m+1)(2k+m-1)=0.

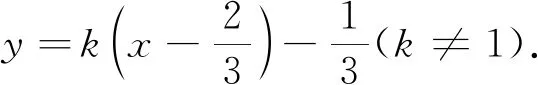
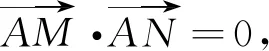
1 命题立意探究

本题的第(2)问是圆锥曲线中的定值问题，但是真正考查的是直线过定点，所以在考场这样一个特定的场合里学生要能够去伪存真，识得庐山真面目，真不是一件容易的事.如果教师在解析几何的二轮复习中注重帮助学生在复杂的环境下寻找规律，抽象出问题的本质，探求问题源头，塑造重要模型，就能够以不变应万变，达到融会贯通.

2 溯源

源头1(2014无锡期末)：

图1

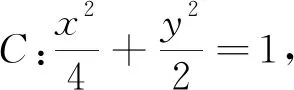
源头2(2017全国卷)：

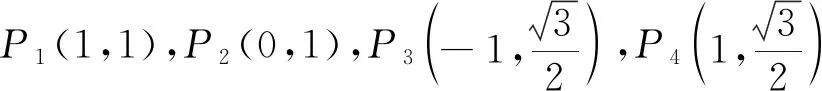
证明(2)设直线P2A与P2B的斜率分别为k1,k2.

3 引流

引流1(2020新课标)：

图2

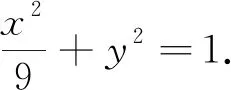
第(2)问：

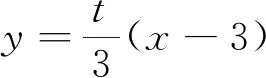
民国时期项氏三十代懿孙项乃斌为重振家声，辑录《嘉善项氏支谱》，但描述的多是清代项氏家族情况，其时已无人再像其先辈那样在鉴藏上有卓越贡献，他们不在本文讨论范围之内，故略去不述。

图3

图4

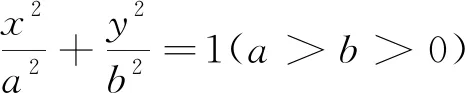
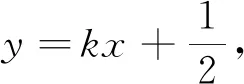
4 高三二轮复习的教学启示

圆锥曲线的综合问题，对学生的思维能力要求非常高，又由于含有字母因而运算量大，所以学生在求解的过程中倍感困惑.在高三的复习课中，教师要充分利用好资源，善于引导学生在问题解决后再研究、再发现，而不是停留在解一道题上，应该引导学生发现对同类问题的共性规律，挖掘题目的内在结构和功能，形成自己的解题模型.

4.1 寻找根源，建立联系

在新《高中数学课程标准》中，数学学科核心素养的水平划分细则里，逻辑推理的最高水平是能够在综合情境中，用数学的眼光找到合适的研究对象，提出有意义的数学问题.2020年的全国卷高考题貌似考查寻找定点Q，如果学生被这个问题牵着鼻子走了，这道压轴高考题就彻底进入了死胡同，进入了出题者的圈套.出题者的本意是考查学生能否在复杂的背景下去伪存真，抽象出直线过定点这一重要模型.如果学生能够识别出来，就说明学生在平时的解析几何学习中善于寻找共性，发现规律，建立解题模型，那么这道高考压轴题就不再压轴了.由此可见，高考题的来源还是在平时的课堂中，并没有高深莫测到无从入手.追溯这道题目的源头，2017年的全国高考卷和2019年的江苏一模卷中都出现了这个直线过定点问题，今年的全国高考题是基于这个问题的解决再往前走了一小步，而这一小步就显得非常简单了.因为直线MN过了定点H，就得到了直角三角形的斜边的两个端点是定点，那么|DQ|这个定值就是直角三角形斜边的中线长，等于斜边的一半，这一步的定点求解利用了平面几何知识.这就需要我们学生有能力在较复杂的数学问题中，通过构建过渡性的命题来探索待论证的结论，并会用严谨的数学语言表达论证和计算的过程.

4.2 优化解法，建立属于自己的解题模型库

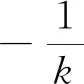
分析源1、源2中的图形，都是经过曲线上一个定点的两条动直线交曲线于两个动点，研究这两个动点所在直线l:y=kx+m过定点的问题.这类问题只要可以表示出这两个动点坐标的等量关系，出现两根之积、两根之和的形式都可以设而不求，用韦达定理来表达，得到k,m之间的等量关系后求出定点.把这样一个模型(以下简称三线一定点)提炼出来，在复杂问题中要能够抽象出具有这样特征的点与线模型，就可以快速解决问题.

4.3 加强探究，自我整合