“隐圆问题处理方法研究”的教学实录与反思*

(江苏省句容高级中学 212400)

在2020届高三进入二轮复习阶段后，为有效提升复习的针对性，句容市教师发展中心召开了以“聚焦微专题，强化关键能力”为主题的高三二轮复习研讨会.笔者应邀开设了一节公开课“隐圆问题处理方法研究”.现将这节课的教学过程、设计意图、课后反思择片段整理成文，不妥之处请各位批评指正.

1 学情分析

本次教学对象是四星级高中的高三物化班学生.学生具备较强的自主学习能力、运算能力和综合运用知识解决问题的能力，但学生平时疏于对知识的归类整理，不屑于对问题追根溯源，更喜欢挑战难度大的压轴题.一轮复习教学时，学生仅在综合练习时零星地遇到过隐圆，没有形成系统的知识体系，故而二轮复习时，笔者通过微专题的形式，从学生知识发展的认知起点和思维发展的生长点出发，将该知识点形成体系，以帮助学生形成解决一类问题的研究方法.

2 考点解读

纵观近几年高考数学江苏卷，隐圆既是考查的热点又是考查的难点，常以压轴填空题或解答题的形式出现，与直线相结合考查直线与圆的位置关系，与三角形相结合考查解析法思想等，尤其是阿波罗尼斯圆，常考常新.隐圆的相关问题实质是解析法在处理平面图形问题中的应用，曲线与方程相互转化，几何直观与代数推理相结合.这些不仅需要学生具有较强的逻辑推理能力和数形结合能力，还需要学生具有良好的数学直觉思维能力，以及较强的代数运算能力.

教学目标 (1)通过对前置作业一般化和学生一起归纳总结出圆的5种常见的形式化定义，完善知识方法体系，体会转化与化归、数形结合的数学思想，提升数学直觉思维能力；(2)通过例1的形异质同题的一题多解、多题一解，例2及变式的题同质异，进一步培养学生的数学直觉思维能力和提升学生通过现象能够发现问题本质的能力；(3)通过隐圆这个小的切口，帮助学生形成解决一类问题的研究方法，积累研究方法的经验.

教学重点 归纳总结出圆的5种常见的形式化定义及其几何特征与代数表达相互转化.

教学难点 圆的5种常见的形式化定义的几何特征与代数表达相互转化.

3 教学实录

3.1 教学片段1——剖析前置作业，追根溯源

题1(苏教版选修2-1第63页例1改编)已知A,B分别是x轴、y轴上的动点，且AB=4，求线段AB的中点M的轨迹方程.

生1：设点M(x,y)，由题意知OM=2，得到点M的轨迹方程是x2+y2=4.

师：点M的轨迹是圆，请给出这个圆的定义.

生1：到定点的距离等于定长的点的集合.

师：大家认可她的看法吗？有什么前提条件吗？

生众：在平面内.

师：(追问)你能用数学符号语言描述你下的定义吗？

生1：在平面内，{M|MA=r}，其中M为动点，A为定点，r>0为定值.

师：接下来答题的同学，请同时给出相应轨迹的定义以及用数学符号语言描述你下的定义.

题2已知点O(0,0),A(1,1)，直线MO,MA的斜率之积为-1，求点M的轨迹方程.

师：还有什么要补充的吗？

生2：点M的轨迹方程里要除去x=0和x=1.

师：(追问)为什么呢？

生2：因为点M的横坐标为0时，MO的斜率不存在；为1时，MA的斜率不存在.

师：这是由斜率的定义决定的.那么你给的定义是不是也要补充？

生2：在平面内，与两定点斜率之积为-1的点的集合(除去定点所在垂直于x轴的直线与曲线的交点). 用数学符号语言描述为：在平面内，{M|kMA·kMB=-1}，其中M为动点，A,B为定点，且点M的横坐标不等于A,B的横坐标.

题3已知点O(0,0),A(1,1)，点M满足MO2+MA2=4，求点M的轨迹方程.

师：表述得非常准确！(追问)λ的取值范围是什么？

生3：λ>0.

师：(再追问)显然λ>0是必要条件，充分吗？

生3：充分.

师：大家同意他的意见吗？

(学生们众说纷纭)

师：如果把问题改为“求实数λ的取值范围”呢？

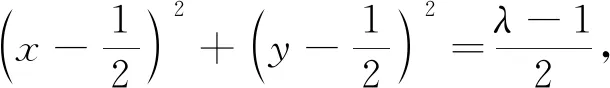
师：由此可见充分必要条件是——

生3：λ>1.

师：你是怎么想到这样处理的呢？

生3：把已知条件坐标化，得到的轨迹方程化简后是圆的标准方程，观察得到λ>1.

师：也就是回到定义上去—坐标化—解析几何的基本思想.若A(a,b),B(c,d)呢？

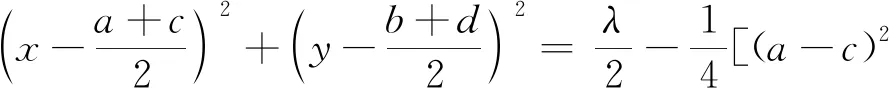
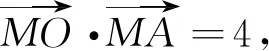
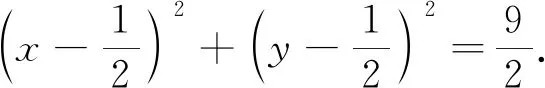
师：若A(a,b),B(c,d)呢？

师：(追问)λ=1时，点M的轨迹是什么？

生5：线段AB的垂直平分线.

问题1如果把圆的第1种形式定义起名为定义圆，那么其余4种定义形式的圆，你可以分别给它们起一个名字吗？

生众：斜率圆、平方圆、向量圆与比值圆(其实比值圆是阿波罗尼斯圆).

问题2这些圆彼此之间有什么联系？

生6：斜率圆可以看成向量圆的特例，即两向量互相垂直时可以转化为两直线斜率之积等于-1.

生7：需要注意斜率不存在的情形.

师：很好！也就是说数量积为零比斜率之积为-1更一般.

生8：比值圆与平方圆是一样的，都是用两点间距离公式求解.

师：生8发现比值圆与平方圆解题所用知识点是一致的.

问题3目前，我们发现圆的五种常见形式化定义，课本为什么用“平面内，到定点距离等于定长的点的集合”作为定义呢？

生8：定义简洁，体现数学的简洁美！

生9：圆的其他的四种形式化简整理后就是“平面内，到定点距离等于定长的点的集合”的数学符号语言表述.

师：说得非常好！大道至简莫过如斯！

设计意图前置作业为容易题，作为课堂教学的起点，以之唤醒学生对即将复习知识的记忆.数学语言的转化是解题的重要前提，文字语言向符号语言转化是学生必备的能力之一，也是学生的薄弱之处.通过追问，一方面培养学生的语言转化能力，另一方面培养学生口头表达的能力.通过追问、反问、再追问，把学生的解题思维“挤”出来：回到圆的标准方程或一般方程确定λ的取值范围，即回到定义上去.问题1引导学生对圆命名，实质上就是贴标签，有助于基础薄弱学生的思维定势，即看到条件有思考的方向，把数学能力转化为数学技能，让“不同的人在数学上得到不同的发展”[1]的基本理念落地生根.通过问题2和问题3的设置，将隐圆的相关知识点整合到同一个概念里，找到隐圆的题根，进而帮助学生获得高阶认知所需的“事实性知识的网络结构”.很显然，这是一种深度学习，体现出核心素养“科学思维”的本质特征.如此被赋予方法论意义，获取余文森教授所指出的“最基础、最具有生长性的关键素养”[2]，促使学生实现由思维层面向素养层面的转化.

3.2 教学片段2——分析例题，剥茧抽丝

例1(2018届南通市、泰州市一模第13题)在平面直角坐标系xOy中，已知点A(-4,0)，B(0,4)，从直线AB上一点P向x2+y2=4引两条切线PC，PD，切点分别为C，D.设线段CD中点为M，则线段AM长的最大值为.

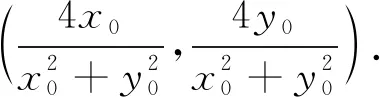
师：这种放弃很明智.用葛军教授的话说，这时应该转场，要么写下一题，要么你换一个角度重新思考.

师：你是怎么想到的？

生11：目标线段AM中A为定点，所以我期望点M的轨迹是圆.而点P在变化的过程中，OP与CD垂直于点M不变，又O为定点，根据“斜率圆”或者“向量圆”的定义，直线CD若过定点，问题就迎刃而解.我就尝试着寻找直线系x0x+y0y=4所过的定点.

师：生10的方法是建立线段AM关于x0的函数关系，转化为函数求最大值问题；生11的方法是利用直线CD过定点，进而得到点M的轨迹是圆，把求线段AM的最大值转化为圆上一动点与圆外一定点距离的最大值问题.前者从代数的角度入手，易想，但难解；后者从几何的角度入手，易解，但难想.不论是代数角度还是几何角度，都是同一个问题的两个方面.

问题4请同学们思考，方法1与方法2有什么联系吗？

师：真精彩！请问你是怎么想到的呢？

生12：根据方法1和方法2的结果凑出来的.(生众笑)

生13：生12的方法就是已知曲线的参数方程求普通方程的方法.

师：生12通过凑来寻找两种不同方法之间联系，靠的是他的数学直觉，这一点非常难能可贵.实际上这是附加题中已知曲线的参数方程求普通方程的常见题型，要用联系的观点，而不是孤立地看问题.大家在一题多解中应多角度比较不同解法之间的联系和区别.这样有助于增强大家对不同解法适用题型的数学直觉，同时也有助于大家对问题有更为立体的认识.

设计意图一题多解培养学生发散性思维.引导学生比较不同解法在处理同一道题目时的优点与不足，帮助学生在理解不同解法的基础上优化解题思路；比较不同解答之间的联系和区别，多解归一.如此加强学生认识问题的深刻性.

3.3 教学片段3——小结课堂，纲举目张

(1)你能归纳一下本节课我们是如何研究隐圆的吗？

(2)你认为我们在应用隐圆时，应注意哪些问题？

(3)你认为一题多解后，做哪些工作可以深化我们对题目以及解法的认识？

设计意图用核心问题组成问题串，促进学生思考，并提纲挈领地归纳总结出本节课研究的问题、所用的研究方法，以及关键细节，以期学生在学习层次和认知水平上得到提升.

4 教学反思

4.1 一点想法

本节课是高三数学二轮微专题复习研讨课.本节课把散落在平时有关圆的定义的问题集中在一起，帮助学生建构相关知识体系.通过对前置作业的5个小题的分析，引导学生猜想、总结出相应的圆的定义形式，并用符号语言表示出来，同时注意相应参数的取值范围，并追问为什么是这个范围，进而引导学生经历知识与方法的过程.在其过程中，建立学生当问题不会处理的时候回到定义上去的意识.在5道小题一般化之后，对其中的圆分别命名.其实比值圆是阿波罗尼斯圆.命名本质是贴标签，有助于学生看到条件有思考的方向，即数学直觉，有利于思维的定势.通过例2与变式的分析(没有来得及)，引导学生发现看似相同的题，实则处理的方法迥然不同.通过对问题的辨析，认识其本质，以防止学生思维过分定势.

4.2 一点争论

有听课教师认为，作为物化班的二轮复习，本节课的教学起点显得过低，应该从综合题入手，提升学生分析问题的能力.但过多地追求题目的难度，就容易忽视大部分学生的现有思维水平和认知结构，教学与学生的试卷相脱节，从而打击学生学习的积极性和自信心.二轮微专题复习教学的教学依然要回归教学的原点，同时把准学生知识发展的认知起点，适当放低起点，以简单的题目为载体，以发展学生思维为主线，厘清分析问题的思路和方法，及时总结并适当延拓至一般情形，找到题根，凸显知识本质，在知识深度理解和能力培养的过程中看准核心素养发展的关键点，提升学生数学核心素养，到达教学高落点.

4.3 一点遗憾

因为学生在课前充分预习并认真解答了学案，所以教师基本上把课堂交给了学生，以学生为主体，把所有的学生卷入课堂，有师生互动、生生互动.结果课堂时间节奏没有把控好，导致教学任务没有完成.对生10例1第(3)题的代数解法，教师直接生硬地借助于生11转到自己预设的轨道上.上课时间虽然紧，但此处不应该追求课堂的容量；应该少一些功利，多一些平和，让学生的解题思维自然地流淌；应该停下来，预设应让位给生成，带领学生一起处理繁重的代数运算.这样，一方面能培养学生坚韧的意志品质，另一方面更加直观地比较两种不同解法的优劣，加深学生用发掘问题中所蕴含的几何条件来降低代数运算的体验，同时让方法的选择更加自然.

4.4 一点困惑

陶维林老师说，学生能处理的就放手，这是教学的一个原则.基于此，二轮复习遵循学生先完成学案，教师批阅并摘录学生不同解法和统计正确率，在此基础上评讲学案，学生订正整理学案的流程.这里存在一种普遍的现象：部分学生会根据自己学案正确与否有选择性地听教师评讲，有时会错过教师的评讲.这种现象显性的是错过教师评讲的过程，隐性的是错过教师对知识点的归纳、对解题思想方法的总结和对一类问题本质的揭示.这就是二轮专题和微专题复习教学中的“滑过”现象.这类问题的解决除了动之以情、晓之以理的苦口婆心的说教外，还有更适切的方法吗？