小学数学中“复习课”教学设计及突围策略

韩辉

【摘  要】复习课作为小学数学课的基本课型之一，是大家研究与关注的内容。它需要学生多种感官与思维的参与，不仅通过回忆对知识进行整理，更要通过迁移知识解决新的问题。所以，小学数学“复习课”的设计要关注在知识、能力上的“突围”。

【关键词】数学教学;小学数学;复习课

中图分类号：G623.5      文献标识码：A      文章编号：0493-2099（2021）10-0074-02

Teaching Design and Breakthrough Strategy of "Review Lesson" in Primary School Mathematics

（Urumqi Education Research Center， Xinjiang Uygur Autonomous Region，China） HAN Hui

【Abstract】As one of the basic course types of primary school mathematics， review class has always been a content of everyone's research， and it is also a problem that plagues everyone. Because it is not as easy to give students the desire to explore like new lectures， nor does it bring students a sense of accomplishment by focusing on solving exercises like practice classes. It requires the participation of students multiple senses and thinking. It not only needs to organize knowledge through memories， but also needs to solve new problems through transfer of knowledge. Therefore， the review class needs to obtain new breakthroughs in terms of knowledge and ability. ".

【Keywords】Mathematics teaching; Elementary school mathematics; Review class

一、復习课目标的“突围”

传统复习课的教学目标大多定位为：1.知识的整理与归纳;2.依托知识展开练习。受应试教育的影响，教师对于复习课的认识还停留在知识层面的回忆与巩固掌握，并没有凸显数学课程标准的精神，学生卷入复习课程度不够深入。

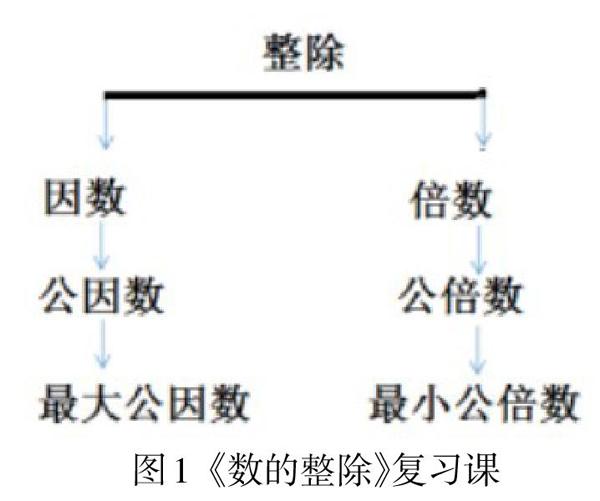
复习中大多数教师仅仅通过回忆的手段帮助学生进行知识的整理是远远不够的，回忆只是在提取头脑中存储的知识，这是低水平的再现。学生在复习中需要将每个知识点串联起来，找到知识间的联系，这才是寻求数学知识本质的有效通道。所以，复习课的应该在“知识的整理与归纳”的基础上进行“突围”，将学生的思维水平从“点状”思维上升为“块状”思维。吴正宪老师在《数的整除》复习课中，通过学生回顾本单元的概念之后，将相关联的概念放在一起的活动，帮助学生织成一张知识“网”（如图1）。用“整除一手托两家”这样的形象化语言，找到“种子概念”因数和倍数，由此派生出其他的相关概念，使学生清楚的梳理出概念间的逻辑关系。

二、复习课设计的“突围”

我们习惯从固定的教学内容、熟悉的教学方法以及常见的教学活动入手设计教学。而缺少从预期的结果、学生的需求入手思考教学。复习课主要有以下的设计方式：1.再将教材上的内容讲一遍，会的学生不愿老调重弹，不会的学生依旧是一地鸡毛，结果是出力不讨好。2.让学生置身题海，做题—讲题—再做题，结果是“教师累够呛，学生急够呛”。3.用回顾、整理知识的方式贯穿复习课始终，结果只有“温故”，缺少“知新”。所以，复习课在设计上需要“突围”。

（一）重视基础考点，适度拓展

设计时首先应该再次回顾课程标准、教学内容、教学的重点难点，预测考试可能涉及的考点以及题型。复习课要对基础知识适度拓展与综合，体现学生数学素养的培养。在“长方体的认识”复习设计中，不能仅仅停留在回忆、梳理知识的层面，更需要从空间想象、推理能力、几何直观的数学能力的培养上下功夫。在教学方式上，对于重要疑难问题可以通过教师讲解、学生探究解决，对于基础性的问题要学会留白，留给学生自行解决，而不必面面俱到。

（二）重视问题解决，提高解题策略

复习课应该在“问题解决”的背景下，向培养学生的解题策略和能力的方向进行“突围”。“解决问题”需要学生具有数学化能力，掌握基本解决问题的策略，形成自我评价与发思能力。运用不同的“解题策略”通过求解各种非单纯的练习题帮助学生较好掌握相关的数学思想与方法。如：在《面积》单元的复习中，设计这样一组题目：

问题1：一个停车场，如果将它的宽增加5米，就变成了一个正方形，这时停车场的面积增加了225平方米，原来停车场的面积是多少平方米？

可以通过“画图”的手段，帮助学生整理信息，理解题意，发现解题的思路。之后，再将这个解题策略进行迁移，解决下面两道题：

问题2：有一个宽35米的长方形停车场，如果宽减少5米，停车场的面积减少了225平方米，现在停车场的面积是多少平方米？