油气状态对车辆油气悬挂特性影响建模分析

刘建辉， 姚方方， 李立琳， 张 彦

(1.黄河交通学院汽车工程学院，河南焦作 450000；2.河南工程学院机械工程系，河南郑州 451191；3.郑州新大方重工科技有限公司，河南郑州 450064)

引言

油气不分离式油气悬挂属于封闭系统，其结构特点决定了其内部油液和气体的状态。油液与气体在结合面直接接触，理想状态时，认为气体不会溶解于油液，实际中却无法忽略气体在油液中的溶解，因此，在环形腔中有可能因为压力降低而析出气体。气体的溶解和析出会改变理想的设计目标，但整体仍表现出气体的特性，对整体的压力变化产生影响[1]。因此，油气悬挂的2个工作腔都有气体存在，假设油液掺混的气体可以与油液分开考虑，将其当作未溶解，据此对油气悬挂的特性进行分析，具有重要应用价值。

国内外学者对此开展了一定的研究，YIN Y等[2]分析不同频率的外载荷作用下，油气悬挂内气体体积的变化规律，以此考察气体溶解性；张军伟等[3]选取不同溶解度的油液进行分析，获取油液溶解对悬挂输出特性的影响；WU W等[4]采用数学建模的方式，分析不同温度下，悬挂内部气体在油液中的溶解比例，以提高模型分析的准确性；KWON K等[5]采用封闭模型，通过压缩气体获取气体在油液中的溶解度。

根据油气悬挂的结构特点，对输出力进行分析；考虑气体在油液中的溶解特性，尤其是工作腔(活塞杆腔)内气体压力的变化导致的腔内的溶解与析出，对气体压力和油液阻尼力进行分析，获取油气悬挂的数学模型；基于Simulink 建立油气悬挂缸的仿真分析模型，根据实际工况，搭建油气悬挂性能分析试验台；在冲击载荷、周期激励及正弦小振幅扫频激励等作用下，对比仿真模型和试验数据获得的簧上质量的位移和压力响应，以此分析气体溶解的影响，并检验模型分析的准确性。

1 油气悬挂模型

1.1 悬挂输出特性分析

油气悬挂的结构，如图1所示。理想状态下，油气悬挂中，仅在工作腔的上部分布着惰性气体，其他部位无气体分布。实际中，由于气体在油液中存在一定的溶解性，随着两腔油液的流动和压力变化，环形腔也会存在少量的气体[6]。气体进入环形腔之后，会因其溶解于油液的特性逐渐减少直至全部溶解，并在环形腔压力降低时析出极少量气体。

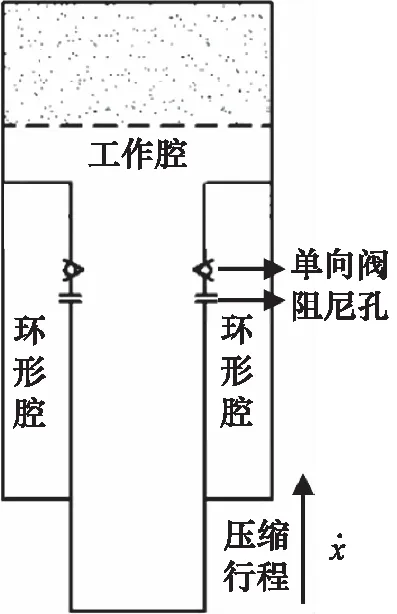
图1 油气悬架结构简图

如图1中所示，环形腔即活塞杆腔压力为p1，面积为A1，气体体积为Vg1，油液体积为Vo1；环形腔压力为p2，面积为A2，气体体积为Vg2，油液体积为Vo2。

悬挂工作时，气体的压力Fg、油液的阻尼力Fz和各部分摩擦力Ff共同作用，根据受力平衡[7]，则输出力为：

F=Fg+Fz+Ff

(1)

根据悬挂的工作原理，两腔的压差为Δpc，则输出力可以写作：

(2)

极小量的气体对悬挂缸的流量及压力影响非常小，可以忽略不计，因此将悬挂缸模型简化为环形腔充满油液[8]，不考虑油液流经阻尼孔产生的压降导致的析出，只考虑活塞杆腔气体压力的变化导致的腔内的溶解与析出。

1.2 内部气体压力分析

在考虑气体溶解到油液对悬挂缸产生的影响时，将悬挂缸的1个行程简化为2个过程[9]，首先不考虑溶解，只考虑气体的压缩，此时悬挂缸由初始的p0，V0变为：

(3)

式中，p0—— 初始气体压力

V0—— 初始气体体积

p1—— 压缩过程后气体压力

Δp—— 压缩过程气体压力变化量

ΔV—— 压缩过程气体体积变化量

惰性气体状态变化采用多变过程描述：

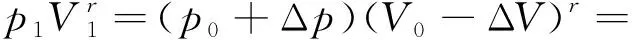
(4)

其中的体积变化可以写作：

ΔV=(A1-A2)x

(5)

则在第1个压缩过程后气体的压强为：

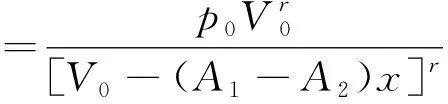
(6)

考虑气体压缩产生压力变化后，压力升高，从而改变了油液对氮气的溶解度，使气体发生了溶解[9]。此溶解过程中，气体的体积不变，依旧为V1=V0-ΔV，但气体的物质的量减少，因此气体的压力要下降。此为1个行程中考虑的第2个过程：

pV=mRgT

(7)

式中，T—— 空气的热力学温度

Rg—— 气体常数

m—— 气体质量

两边求导得：

Δp′·V1=Δm·RgT

(8)

式中，Δp′—— 压缩过程气体压力变化量

Δm—— 溶解过程中溶解的气体质量

由溶解度方程可得，溶解的气体质量为：

(9)

式中，δ—— 任意压力下气体的溶解度

patm—— 标准大气压力

V01—— 气体体积

ρ—— 气体密度

代入上式得：

(10)

则：

(11)

综上可得：

(12)

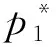
则悬挂缸的弹性力为：

(13)

1.3 阻尼力分析

忽略环形腔油液的可压缩性，将其视为刚性体，则通过阻尼孔和单向阀的流量由环形腔的体积变化速率决定[10]。

拉伸时通过2个阻尼孔的流量为：

(14)

压缩时油液流经阻尼孔的流量为：

(15)

式中，A2—— 环形腔面积

Cd,Cz—— 阻尼孔、单向阀的流量系数

Ad,Az—— 阻尼孔、单向阀的过流面积

Δpc—— 两腔的的压力差

则拉伸行程时两腔压差为：

(16)

此时，环形腔压力为：

(17)

此时，整个悬挂缸的阻尼力为：

(18)

压缩行程时两腔压差为：

(19)

此时，环形腔压力为：

此时，悬挂缸的阻尼力为：

(21)

1.4 油气悬挂数学模型

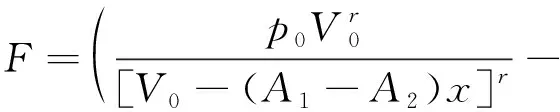
(22)

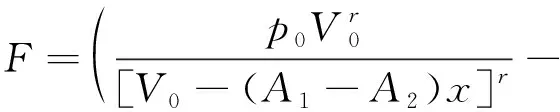
(23)

2 油气悬挂分析模型和试验台

根据数学模型，基于Simulink 建立油气悬挂缸的仿真分析模型，如图2所示。系统的输入信号为正弦激励，激励频率与振幅可改变，输出端为活塞杆腔压力、活塞杆腔面积、环形腔压力、环形腔面积以及摩擦力，计算出悬挂缸输出力，即得到簧上质量的运动规律[11-12]。并将其反馈至输入激励处，即构成本模型总体结构，这个结构是符合悬挂缸真实工况的。

图2 油气悬挂仿真模型

根据油气悬挂的实际工作状态，参考1/4车辆模型，搭建如图3a所示的试验台。整体台架分为上、下两部分，上部为加载装置，下部为试验油气悬挂，通过力和位移传感器获取相关参数变化。液压系统配备换向阀[13]，实现加载装置换向，改变油气悬架的加载方向，传感器获取输出力和位移的变化，油气悬架实物图如图3b所示。

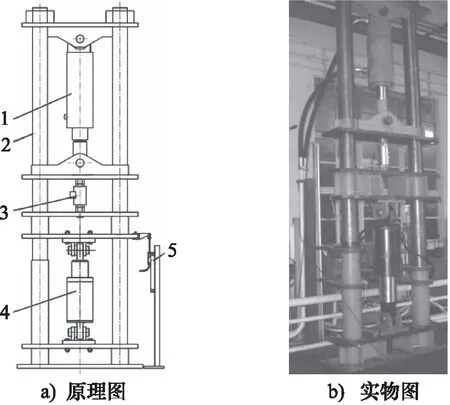
1.加载缸 2.支撑架 3.力传感器4.油气悬挂 5.位移传感器图3 油气悬挂试验台

3 不同加载下特性对比分析

3.1 冲击载荷激励

操纵液压系统，提升簧上质量位置，进行固定，同时增加簧上载荷大小，之后释放[14]。初始状态，油气悬挂的充油体积4.6 L，充气至缸筒活塞杆相对位移127.5 mm。冲击载荷作用下，仿真和试验对比结果如图4所示。

图4 冲击载荷激励作用结果

由图4可知，簧上质量开始做自由落体运动，之后由于油液的衰减作用，逐渐达到平衡位置，仿真分析变化过程与试验测试基本一致，1.5 s左右达到平衡状态，试验时平衡位置位移为0.045 mm，仿真值为0.047 mm，误差小于3%。频谱分析可知，0.65 Hz 左右幅度Vp达到峰值位置，试验峰值为0.0066 mm，而仿真分析的峰值为0.0065 mm，前者的能量总量更多，频谱分析更为广泛。分析差异的原因主要是，整个过程时间较短，气体状态参数发生变化，而模型中忽略了相关变化；试验设备设置摩擦保护装置，对结果也产生一定的影响。

3.2 周期性激励

初始状态，油气悬挂的充油体积4.6 L，充气至缸筒活塞杆相对位移127.5 mm。对系统施加周期性激励，其振幅5 mm，频率1.5 Hz，获取周期性激励作用下位移和压力变化曲线，如图5所示。在周期性激励作用下，运动位移和气体压力的仿真结果与试验测试数据一致，最大误差范围在1 mm内；气体压力响应误差范围在0.06 MPa内，表明数学模型的准确性。

图5 周期性激励作用结果

3.3 正弦小振幅扫频激励

悬挂充油、充气后，持续不间断运行工作[15]，由1.2 Hz匀速变化至3 Hz，连接传感器，采集所有需要的数据，试验和仿真分析获取的簧上质量位移如图6所示。整个加载过程约800 s，经过扫频作用后，簧上质量平衡位置由原来的-0.0015 m，分别下降至-0.0187 m和-0.0182 m，分别下降了0.0172 m和0.0167 m，二者相差0.5 mm；试验分析和仿真分析中，振幅也发生了衰减，前者由4.5 mm降低至1.5 mm，后者由4.5 mm逐渐降低至1.6 mm，对比变化趋势可以发现，低阶频率时，二者基本一致，高阶频率时，存在一定差异，差值约为7%。

采用短时傅里叶(STFT)变换对图6所得结果进行分析，获得如图7所示的分析结果。试验和仿真获取的位移变化，整体变化趋势是一致的。系统受到激励作用以外，还受到内部特性的作用，在试验和仿真中均可观察到，主要是高频信号的作用。

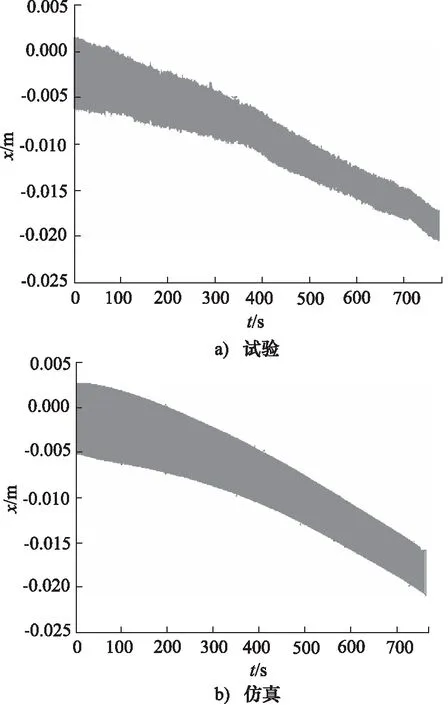
图6 簧上质量位移对比

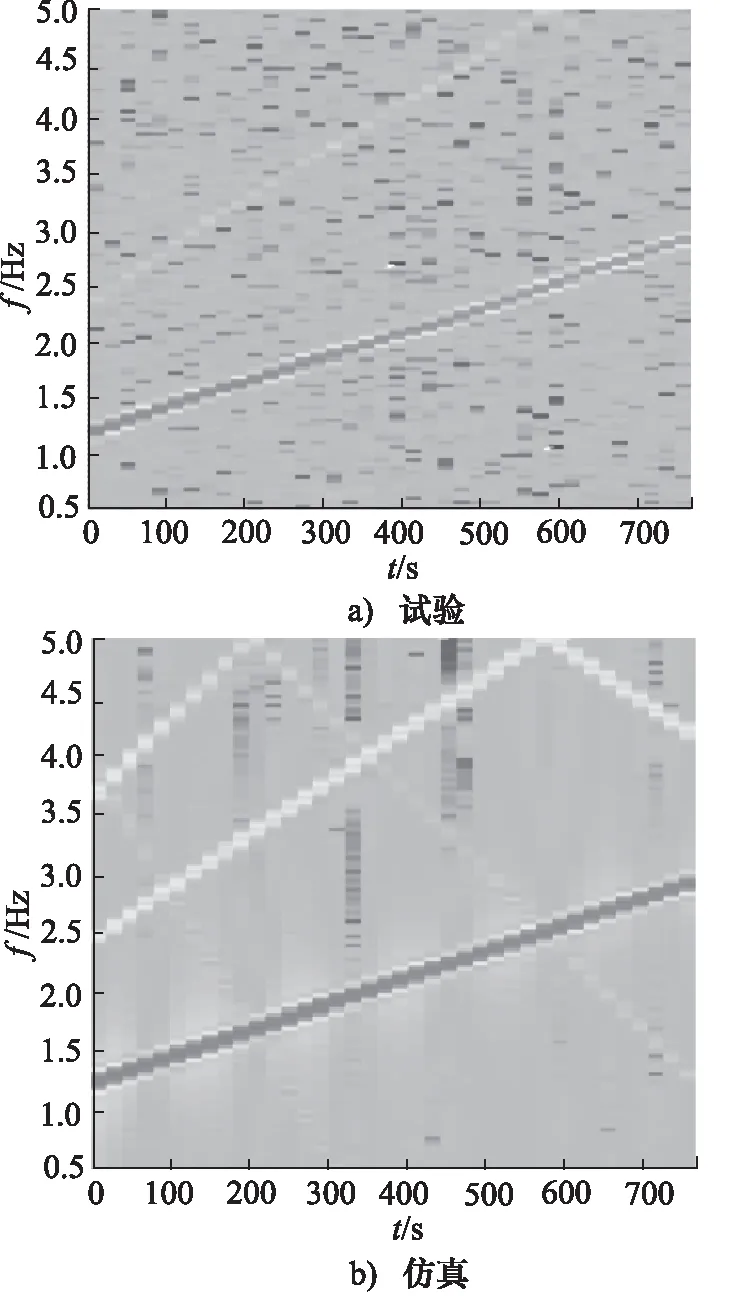
图7 频谱分析结果对比

对两种模型的振动传递率ηx进行分析，变化曲线如图8所示。在施加的扫频激励作用下，传递率均小于1，系统的性能满足要求。频率增加时，性能进一步提升。试验结果和仿真分析变化趋势基本一致，误差在8%以内。

图8 位移传递率

4 结论

(1) 冲击载荷作用时，1.5 s左右达到平衡状态，试验时平衡位置位移为0.045 m，仿真值为0.047 m，误差小于3%；

(2) 在周期性激励作用下，运动位移和气体压力的仿真结果与试验测试数据一致，运动位移最大误差范围在 1 mm内，气体压力响应误差范围在0.06 MPa内；

(3) 在施加扫频激励作用下，传递率均小于1，系统性能满足要求，试验结果和仿真分析变化趋势基本一致，误差在8%以内；

(4) 气体溶解于油液的特性会影响悬挂缸的外特性，不同激励分析结果的一致性表明，溶解性能的数学模型的准确性在设计分析时需要加以考虑。